4.1 Creating and Using a Statistic
The Statistic class has a great deal of functionality. It accumulates summary statistics on the values presented to it via its collect methods. Recall also that since the Statistic class implements the CollectorIfc interface, you can use the reset() method to clear all accumulated statistics and reuse the Statistic instance. The major statistical quantities are found in the StatisticAccessor interface.
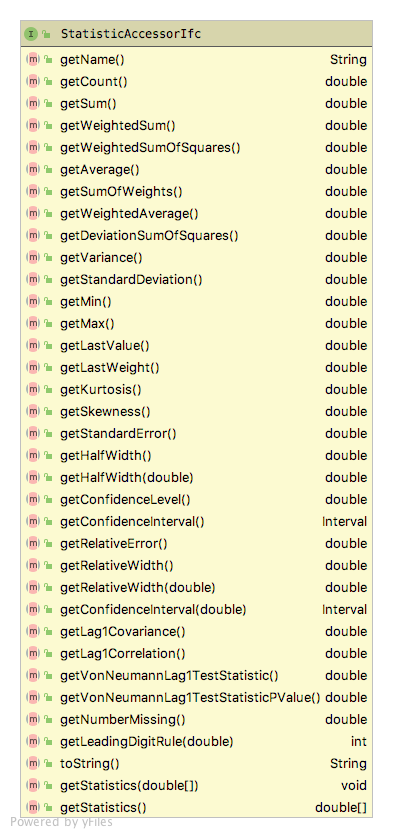
Figure 4.3: Major Accumulated Statistical Quantities
As can be seen in Figure 4.3, the Statistic class not only computes the standard statistical quantities such as the count, average, and variance, it also has functionality to compute confidence intervals, skewness, kurtosis, the minimum, the maximum, and lag 1 covariance and correlation. The computed confidence intervals are based on the assumption that the observed data are normally distributed or that the sample size is large enough to justify using the central limit theorem to assume that the sampling distribution is normal. Thus, we can assume that the confidence intervals are approximate. The summary statistics are computed via efficient one pass algorithms that do not require any observed data to be stored. The algorithms are designed to minimize issues related to numerical precision within the calculated results. The toString() method of the Statistic class has been overridden to contain all of the computed values. Let’s illustrate the usage of the Statistic class with some code. In this code, first we create a normal random variable to be able to generate some data. Then, two statistics are created. The first statistic directly collects the generated values. The second statistic is designed to collect \(P(X\geq 20.0)\) by observing whether or not the generated value meets this criteria as defined by the boolean expression x >= 20.0.
// create a normal mean = 20.0, variance = 4.0 random variable
NormalRV n = new NormalRV(20.0, 4.0);
// create a Statistic to observe the values
Statistic stat = new Statistic("Normal Stats");
Statistic pGT20 = new Statistic("P(X>=20");
// generate 100 values
for (int i = 1; i <= 100; i++) {
// getValue() method returns generated values
double x = n.getValue();
stat.collect(x);
pGT20.collect(x >= 20.0);
}
System.out.println(stat);The results for the statistics collected directly on the observations from the toString() method are as follows.
ID 1
Name Normal Stats
Number 100.0
Average 20.370190128861807
Standard Deviation 2.111292233346322
Standard Error 0.2111292233346322
Half-width 0.4189261806189412
Confidence Level 0.95
Confidence Interval [19.951263948242865, 20.78911630948075]
Minimum 15.020744984423821
Maximum 25.33588436770212
Sum 2037.0190128861807
Variance 4.457554894588499
Weighted Average 20.370190128861797
Weighted Sum 2037.0190128861796
Sum of Weights 100.0
Weighted Sum of Squares 41935.76252316213
Deviation Sum of Squares 441.2979345642614
Last value collected 21.110736402119805
Last weighted collected 1.0
Kurtosis -0.534855387072145
Skewness 0.20030433873223502
Lag 1 Covariance -0.973414579833684
Lag 1 Correlation -0.22057990840016864
Von Neumann Lag 1 Test Statistic -2.2136062395518343
Number of missing observations 0.0
Lead-Digit Rule(1) -1Of course, this is probably more output than what you need, but you can use the methods illustrated in Figure 4.3 to access specific desired quantities. Notice that in the code example that the \(P(X \geq 20.0)\) is also collected. This is done by using the boolean expression x >= 20.0 within the collect() method. This expression evaluates to either true or false. The true values are presented as 1.0 and the false values as 0.0. Thus, this expression acts as an indicator variable and facilitates the estimation of probabilities. The results from the statistics can be pretty printed by using the StatisticReporter class, which takes a list of objects that implement the StatisticAccessorIfc interface and facilitates the writing and printing of various statistical summary reports.
StatisticReporter reporter = new StatisticReporter(List.of(stat, pGT20));
System.out.println(reporter.getHalfWidthSummaryReport());Half-Width Statistical Summary Report - Confidence Level (95.000)%
Name Count Average Half-Width
----------------------------------------------------------------------------------------------------
Normal Stats 100 20.3702 0.4189
P(X>=20 100 0.5100 0.0997
---------------------------------------------------------------------------------------------------- The Statistic class has a number of very useful static methods that work on arrays and compute various statistical quantities.
int getIndexOfMin(double[] x)- returns the index of the element that is smallest. If there are ties, the first found is returned.double getMin(double[] x)- returns the element that is smallest. If there are ties, the first found is returned.int getIndexOfMax(double[] x)- returns the index of the element that is largest If there are ties, the first found is returned.double getMax(double[] x)- returns the element that is largest. If there are ties, the first found is returned.double getMedian(double[] data)- returns the value that has 50 percent of the data above and below it.int countLessEqualTo(double[] data, double x)- returns the count of the elements that are less than or equal to \(x\)int countLessThan(double[] data, double x)- returns the count of the elements that are less than \(x\)int countGreaterEqualTo(double[] data, double x)- returns the count of the elements that are greater than or equal to \(x\)int countGreaterThan(double[] data, double x)- returns the count of the elements that are greater than \(x\)double[] getOrderStatistics(double[] data)- returns a sorted copy of the supplied array ordered from smallest to largest- long estimateSampleSize(double desiredHW, double stdDev, double level)` - returns the approximate sample size necessary to reach the desired half-width at the specified confidence level given the estimate of the sample standard deviation.
Statistic collectStatistics(double[] x, double[] w)- returns an instance ofStatisticthat summarizes the array of values and the supplied weights.collectStatistics(double[] x)- returns an instance ofStatisticthat summarizes the array of values