6.5 Modeling DEDS in the JSL
Discrete event modeling within the JSL is facilitated by two packages:
1) the jsl.simulation package and 2) the jsl.calendar package. The jsl.simulation
package has classes that implement behavior associated with simulation
events and models. The jsl.calendar package has classes that facilitate the
scheduling and processing of events.
6.5.1 Event Scheduling
The following classes within the jsl.simulation package work together to
provide for the scheduling and execution of events:
Simulation- An instance of Simulation holds the model and facilitates the running of the simulation according to run parameters such as simulation run length and number of replications.Executive- The Executive controls the execution of the events and works with the calendar package to ensure that events are executed and the appropriate model logic is called at the appropriate event time. This class is responsible for placing the events on a calendar, allowing events to be canceled, and executing the events in the correct order.JSLEvent– This class represents a simulation event. The attributes of JSLEvent provide information about the name, time, priority, and type of the event. The user can also check whether or not the event is canceled or if it has been scheduled. In addition, a general attribute of type Object is associated with an event and can be used to pass information along with the event.ModelElement– This class serves as a base class for all classes that are within a simulation model. It provides access to the scheduler and ensures that model elements participate in common simulation actions (e.g. warm up, initialization, etc.).Model- An instance of a Model is required to serve as the parent to any model elements within a simulation model. It is the top-level container for model elements.SchedulingElement– SchedulingElement is a sub-class of ModelElement and facilitates the scheduling of events within a simulation model. Classes that require significant event scheduling should sub-class from SchedulingElement.
Figure 6.5 illustrates the relationships between the
classes Model, ModelElement, SchedulingElement, Simulation, and
Executive. The ModelElement class represents the primary building block
for JSL models. A ModelElement represents something (an element) that
can be placed within an instance of a Model. The Model class subclasses
ModelElement. Every ModelElement can contain many other instances of
ModelElement. As such, an instance of a Model can also contain model
elements. There can only be one instance of the Model class within the
simulation. It acts as the parent (container) for all other model
elements. Model elements in turn also hold other model elements.
Instances arranged in this pattern form an object hierarchy that
represents the simulation model. The instance of a Simulation holds
(references) the instance of the Model class. Simulation also references
the Executive. The instance of the Executive uses an instance of a class
that implements the CalendarIfc interface. The simulation also
references an instance of the Experiment class. The Experiment class
allows the specification and control of the run parameters for the
simulation. Every instance of a ModelElement must be a child of another
ModelElement or the Model. This implies that instances of ModelElement
have access to the main model, which has access to an instance of
Simulation and thus the instance of the Executive. Therefore sub-classes
of ModelElement have access to the Executive and can schedule events.
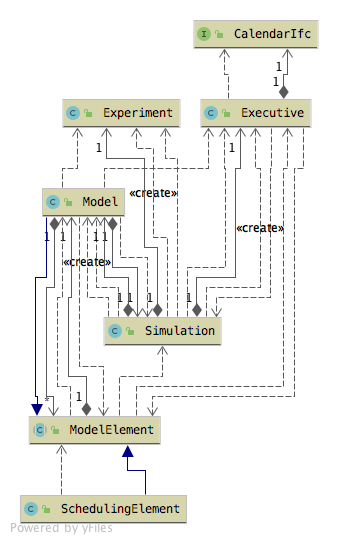
Figure 6.5: jsl.simulation Package and Relationships
The SchedulingElement class is a special kind of ModelElement that
facilitates the scheduling of events. SchedulingElement is an abstract
base class for building other classes that schedule events. Sub-classes
of the SchedulingElement class will have a set of methods that
facilitate the scheduling of events.
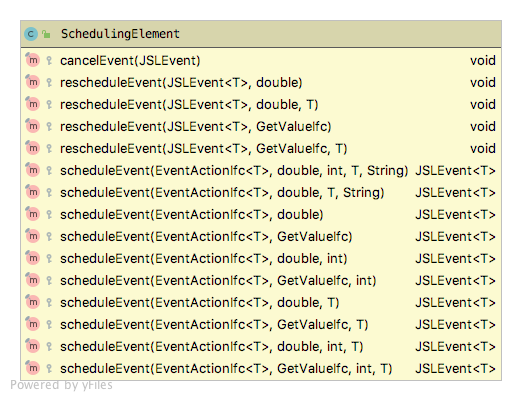
Figure 6.6: SchedulingElement and its scheduling methods
Figure 6.6 illustrates the protected methods of
the SchedulingElement class. Since these methods are protected,
sub-classes will have them available through inheritance. There are two
major types of scheduling methods: one for rescheduling already existing
events and another for scheduling new events. The scheduling of new
events results in the creation of a new JSLEvent and the placement of
the event on the event calendar via the Executive.
The following code listing illustrates the key method for
scheduling events within the class SchedulingElement. Notice that the instance of the Executive is called via getExecutive(). In addition, the user can supply information for the
creation of an event such as its time, name, and priority. The user can
also provide an instance of classes that implement the EventActionIfc
interface. This interface promises to have an action() method. Within
the action() method the user can provide the code that is necessary to
represent the state changes associated with the event.
/** Creates an event and schedules it onto the event calendar. This is the main scheduling method that
* all other scheduling methods call. The other methods are just convenience methods for this method.
*
* @param <T> the type associated with the attached message
* @param action represents an ActionListener that will handle the change of state logic
* @param time represents the inter-event time, i.e. the interval from the current time to when the
* event will need to occur
* @param priority is used to influence the ordering of events
* @param message is a generic Object that may represent data to be transmitted with the event
* @param name the name of the event
* @return a valid JSLEvent
*/
protected final <T> JSLEvent<T> scheduleEvent(EventActionIfc<T> action, double time, int priority, T message, String name) {
JSLEvent<T> event = getExecutive().scheduleEvent(action, time, priority, message, name, this);
return (event);
}There are two ways that the user can
provide event action code: 1) provide a class that implements the
EventActionIfc interface and supply it when scheduling the event or 2)
by treating the EventActionIfc as a functional interface and using Java 8’s functional method representation. Providing an inner class that implements the EventActionIfc interface will be illustrated here.
6.5.2 Simple Event Scheduling Examples
This section presents two simple examples to illustrate event
scheduling. The first example illustrates the scheduling of events using the EventActionIfc interface. The second example shows how to simulate a Poisson process and collect
simple statistics.
6.5.2.1 Implementing Event Actions Using the EventActionIfc Interface
In the first example, there will be two events scheduled with actions. The time between the events will all be deterministic. The specifics of the events are as follows:
- Event Action One: This event occurs only once at time 10.0 and schedules the Action Two event to occur 5.0 time units later. It also prints out a message.
- Event Action Two: This event prints out a message. Then, it schedules an action one event 15 time units into the future. It also reschedules itself to reoccur in 20 minutes.
The following code listing provides the code for this simple event example. Let’s walk carefully through the construction and execution of this code.
First, the class sub-classes from SchedulingElement. This
enables the class to have access to all the scheduling methods within
SchedulingElement and provides one method that needs to be overridden:
initialize(). Every ModelElement has an initialize()
method. The base class, ModelElement’s initialize() method does nothing.
However, the initialize() method is critical to properly modeling
using instances of ModelElement within the JSL architecture. The purpose of the
initialize() method is to provide code that can occur once at the
beginning of each replication of the simulation, prior to the execution
of any events. Thus, the initialize() method is the perfect location to
schedule initial events onto the event calendar so that when the
replications associated with the simulation are executed initial events
will be on the calendar ready for execution. Notice that in this example
the initialize() method does two things:
- schedules the first event action one event at time 10.0 via the call: scheduleEvent(myEventActionOne, 10.0)
- schedules the first action two event at time 20.0 via the call: scheduleEvent(myEventActionTwo, 20.0)
public class SchedulingEventExamples extends SchedulingElement {
private final EventActionOne myEventActionOne;
private final EventActionTwo myEventActionTwo;
public SchedulingEventExamples(ModelElement parent) {
this(parent, null);
}
public SchedulingEventExamples(ModelElement parent, String name) {
super(parent, name);
myEventActionOne = new EventActionOne();
myEventActionTwo = new EventActionTwo();
}
@Override
protected void initialize() {
// schedule a type 1 event at time 10.0
scheduleEvent(myEventActionOne, 10.0);
// schedule an event that uses myEventAction for time 20.0
scheduleEvent(myEventActionTwo, 20.0);
}
private class EventActionOne extends EventAction {
@Override
public void action(JSLEvent event) {
System.out.println("EventActionOne at time : " + getTime());
}
}
private class EventActionTwo extends EventAction {
@Override
public void action(JSLEvent jsle) {
System.out.println("EventActionTwo at time : " + getTime());
// schedule a type 1 event for time t + 15
scheduleEvent(myEventActionOne, 15.0);
// reschedule the EventAction event for t + 20
rescheduleEvent(jsle, 20.0);
}
}
public static void main(String[] args) {
Simulation s = new Simulation("Scheduling Example");
new SchedulingEventExamples(s.getModel());
s.setLengthOfReplication(100.0);
s.run();
}
}The call scheduleEvent(myEventAction, 20.0) schedules an event 20 time
units into the future where the event will be handled via the instance
of the class EventActionTwo, which implements the EventActionIfc interface.
The reference myEventActionTwo refers to an object of type EventActionTwo,
which is an instance of the inner classes defined within
SchedulingEventExamples. This variable is defined as as class attribute
on line 4 and an instance is created in the constructor on line 11. To
summarize, the initialize() method is used to schedule the initial occurances of the two types of events. The initialize() method occurs right before time 0.0. That is, it occurs right before the simulation clock starts.
Now, let us examine the actions that occur for the two types of events. Within the action() method of EventActionOne, we see the following code:
System.out.println("EventActionOne at time : " + getTime());Here a simple message is printed that includes the simulation time via the inherited getTime() method of the ModelElement class. Thus, by implementing the action() method of the EventActionIfc interface, you can supply the logic that occurs when the event is executed by the simulation executive. In the implemented EventActionTwo class, a simple message is printed and event action one is scheduled. In addition, the rescheduleEvent() method is used to reschedule the event that was supplied as part of the action() method. Since the attributes of the event remain the same,
the event is “recycled” to occur at the new scheduled time.
The main method associated with the SchedulingEventExamples class
indicates how to create and run a simulation model. The first line of the main method creates an instance of a Simulation. The next line makes an instance of
SchedulingEventExamples and attaches it to the simulation model. The
method call, s.getModel() returns an instance of the Model class that is
associated with the instance of the Simulation. The next line sets up the
simulation to run for 100 time units and the last line tells the simulation to
begin executing via the run() method. The output of the code is as follows:
EventActionOne at time : 10.0
EventActionTwo at time : 20.0
EventActionOne at time : 35.0
EventActionTwo at time : 40.0
EventActionOne at time : 55.0
EventActionTwo at time : 60.0
EventActionOne at time : 75.0
EventActionTwo at time : 80.0
EventActionOne at time : 95.0
EventActionTwo at time : 100.0Notice that event action one output occurs at time 10.0. This is due to the event that was scheduled within the initialize() method. Event action two occurs for the first time at time 20.0 and then every 20 time units. Notice that event action one occurs at time 35.0. This is due to the event being scheduled in the action method of event action two.
6.5.2.2 Overview of Simuation Run Context
When the simulation runs, much underlying code is executed. At this
stage it is not critically important to understand how this code works;
however, it is useful to understand, in a general sense, what is
happening. The following outlines the basic processes that are occurring
when s.run() occurs:
Setup the simulation experiment
For each replication of the simulation:
Initialize the replication
Initialize the executive and calendar
Initialize the model and all model elements
While there are events on the event calendar or the simulation is not stopped
Determine the next event to execute
Update the current simulation time to the time of the next event
Call the action() method of the instance of
EventActionIfcthat was attached to the next event.Execute the actions associated with the next event
Execute end of replication model logic
Execute end of simulation experiment logic
Step 2(b) initializes the executive and calendar and ensures that there
are no events at the beginning of the simulation. It also resets the
simulation time to 0.0. Then, step 2(c) initializes the model. In this
step, the initialize() methods of all of the model elements are
executed. This is why it was important to implement the initialize()
method in the example and have it schedule the initial events. Then,
step 2(c) begins the execution of the events that were placed on the
calendar. In looking at the code listings, it is not possible to ascertain how the action() methods are actually invoked unless you
understand that during step 2(c) each scheduled event is removed from
the calendar and its associated action called. In the case of the event action one
and two events in the example, these actions are specified in the action() method of EventActionOne and EventActionTwo. After all the events in the
calendar are executed or the simulation is not otherwise stopped, the
replication is ended. Any clean up logic (such as statistical
collection) is executed at the end of the replication. Finally, after
all replications have been executed, any logic associated with ending
the simulation experiment is invoked. Thus, even though the code does
not directly call the event logic it is still invoked by the simulation
executive because the events are scheduled. Thus, if you schedule
events, you can be assured that the logic associated with the events
will be executed.
6.5.2.3 Simulating a Poisson Process
The second simple example illustrates how to simulate a Poisson process. Recall that a Poisson process models the number of events that occur within some time interval. For a Poisson process the time between events is exponentially distributed with a mean that is the reciprocal of the rate of occurrence for the events. For simplicity, this example simulates a Poisson process with rate 1 arrival per unit time. Thus, the mean time between events is 1.0 time unit. In this case the action is very simple, incrementing a counter that is tracking the number of events that have occurred.
The code for this example is as follows.
public class SimplePoissonProcess extends SchedulingElement {
private final RandomVariable myTBE;
private final Counter myCount;
private final EventHandler myEventHandler;
public SimplePoissonProcess(ModelElement parent) {
this(parent, null);
}
public SimplePoissonProcess(ModelElement parent, String name) {
super(parent, name);
myTBE = new RandomVariable(this, new ExponentialRV(1.0));
myCount = new Counter(this, "Counts events");
myEventHandler = new EventHandler();
}
@Override
protected void initialize() {
scheduleEvent(myEventHandler, myTBE.getValue());
}
private class EventHandler extends EventAction {
@Override
public void action(JSLEvent evt) {
myCount.increment();
scheduleEvent(myEventHandler, myTBE.getValue());
}
}
public static void main(String[] args) {
Simulation s = new Simulation("Simple PP");
new SimplePoissonProcess(s.getModel());
s.setLengthOfReplication(20.0);
s.setNumberOfReplications(50);
s.run();
SimulationReporter r = s.makeSimulationReporter();
r.printAcrossReplicationSummaryStatistics();
System.out.println("Done!");
}
}There are a few new elements of this code to
note. First, this example uses two new JSL model elements:
RandomVariable and Counter. A RandomVariable is a sub-class of
ModelElement that is used to represent random variables within a
simulation model. The RandomVariable class must be supplied an instance
of a class that implements the RandomIfc interface. Recall that
implementations of the RandomIfc interface have a getValue() method that
returns a random value and permit random number stream control. The
supplied stream control is important when utilized advanced simulation
statistical methods. For example, stream control is used to advance the
state of the underlying stream to the next substream at the end of every
replication of the model. This helps in synchronizing the use of random
numbers in certain types of experimental setups.
A Counter is also a sub-class of ModelElement which facilitates the incrementing and
decrementing of a variable and the statistical collection of the
variable across replications. The value of the variable associated with
the instance of a Counter is automatically reset to 0.0 at the beginning
of each replication. Lines 2 and 3 within the constructor create the
instances of the RandomVariable and the Counter.
Since we are modeling a Poisson process, the initialize() method is used
to schedule the first event using the random variable that represents
the time between events. This occurs on the only line of the initialize() method. The event logic, found in the inner class EventHandler,
causes the counter to be incremented. Then, the next arrival is scheduled
to occur. Thus, it is very easy to model an arrival process using this
pattern. The last items to note are in the main() method of the class,
where the simulation is created and run. In setting up the simulation,
the run length is set to 20 time units and the number of
replications associated with the simulation is set to 50.
A replication represents a sample path of the simulation that starts and ends under the same conditions. Thus, statistics collected on each replication represent independent and identically distributed observations of the simulation model’s execution. In this example, there will be 50 observations of the counter observed. Since we have a Poisson process with rate 1 event per time unit and we are observing the process for 20 time units, we should expect that about 20 events should occur on average.
Right after the run() method is called, an instance of a SimulationReporter is created for the
simulation. A SimulationReporter has the ability to write out
statistical output associated with the simulation. The code uses the
printAcrossReplicationSummaryStatistics() method to write out a simple
summary report across the 50 replications for the Counter. Note that
using the Counter to count the events provided for automatically
collected statistics across the replications for the counter. As you can
see from the output, the average number of events is close to the
theoretically expected amount.
Across Replication Statistical Summary Report
Sat Dec 31 13:02:53 EST 2016
Simulation Results for Model: Simple PP_Model
Number of Replications: 50
Length of Warm up period: 0.0
Length of Replications: 20.0
-----------------------------------------------------------
Counters
-----------------------------------------------------------
Name Average Std. Dev. Count
-----------------------------------------------------------
Counts events 20.500000 4.870779 50.000000
-----------------------------------------------------------6.5.3 Up and Down Component Example
This section further illustrates DEDS modeling with a component of a system that is subject to random failures. The component has two states UP and DOWN. The time until failure is random and governed by an exponential distribution with a mean of 1.0 time units. This represents the time that the component is in the UP state. Once the component fails, the component goes into the DOWN state. The time that the component spends in the DOWN state is governed by an exponential distribution with a mean of 2.0 time units. In this model, we are interested in estimating the proportion of time that the component is in the UP state and tracking the number of failures over the running time of the simulation. In addition, we are interested in measuring the cycle length of the component. The cycle length is the time between entering the UP state. The cycle length should be equal to the sum of the time spent in the up and down states.
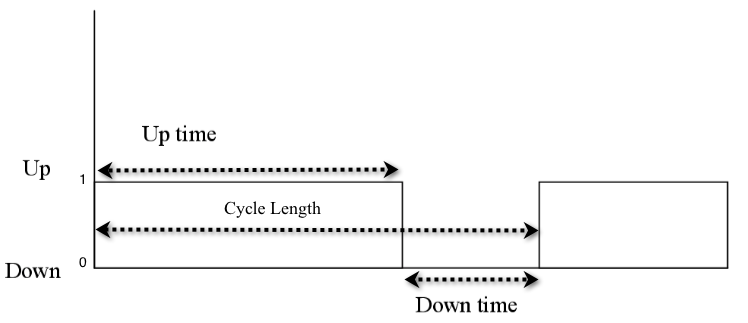
Figure 6.7: Up and Down Component Process
Figure 6.7 illustrates the dynamics of the component over time.
The following steps are useful in developing this model:
- Conceptualize the system/objects and their states
- Determine the events and the actions associated with the events
- Determine how to represent the system and objects as ModelElements
- Determine how to initialize and run the model
The first step is to conceptualize how to model the system and the state
of the component. A model element, UpDownComponent, will be used to
model the component. To track the state of the component, it is
necessary to know whether or not the component is UP or DOWN. A variable
can be used to represent this state. However, since we need to estimate
the proportion of time that the component is in the UP state, a
TimeWeighted variable will be used. TimeWeighted is a sub-class of
ModelElement that facilitates the observation and statistical collection
of time-based variables. Time-bases variables, which are discussed
further in the next Chapter, are a type of variable that changes values
at particular instants of time. Time-based variables must have
time-weighted statistics collected. Time-weighted statistics weights the
value of the variable by the proportion of time that the variable is set
to a value. To collect statistics on the cycle length we can use a
ResponseVariable. ResponseVariable is a sub-class of ModelElement that
can take on values within a simulation model and allows easy statistical
observation of its values during the simulation run. This class provides
observation-based statistical collection. Further discussion of
observation-based statistics will be presented in the next Chapter.
Because this system is so simple the required performance measures can be easily computed theoretically. According to renewal theory, the probability of being in the UP state in the long run should be equal to:
\[P(UP) = \frac{\theta_{u}}{\theta_{u}+\theta_{d}} = \frac{1.0}{1.0+2.0}=0.\overline{33}\]
where \(\theta_{u}\) is the mean of the up-time distribution and \(\theta_{d}\) is the mean of the down-time distribution. In addition, the expected cycle length should be \(\theta_{u}+\theta_{d} = 3.0\).
The UpDownComponent class extends the SchedulingElement class and has
object references to instances of RandomVariable, TimeWeighted,
ResponseVariable, and Counter classes. Within the constructor of
UpDownComponent, we need to create the instances of these objects for
use within the class, as shown in the following code fragment.
public class UpDownComponent extends SchedulingElement {
public static final int UP = 1;
public static final int DOWN = 0;
private RandomVariable myUpTime;
private RandomVariable myDownTime;
private TimeWeighted myState;
private ResponseVariable myCycleLength;
private Counter myCountFailures;
private final UpChangeAction myUpChangeAction = new UpChangeAction();
private final DownChangeAction myDownChangeAction = new DownChangeAction();
private double myTimeLastUp;
public UpDownComponent(ModelElement parent) {
this(parent, null);
}
public UpDownComponent(ModelElement parent, String name) {
super(parent, name);
RVariableIfc utd = new ExponentialRV(1.0);
RVariableIfc dtd = new ExponentialRV(2.0);
myUpTime = new RandomVariable(this, utd, "up time");
myDownTime = new RandomVariable(this, dtd, "down time");
myState = new TimeWeighted(this, "state");
myCycleLength = new ResponseVariable(this, "cycle length");
myCountFailures = new Counter(this, "count failures");
}Lines 3 and 4 define two constants to represent
the up and down states. Lines 5-9 declare additional references
needed to represent the up and down time random variables and the
variables that need statistical collection (myState, myCycleLength, and
myCountFailures). Lines 10 and 11 define and create the event actions
associated with the end of the up-time and the end of the down time. The
variable myTimeLastUp is used to keep track of the time that the
component last changed into the UP state, which allows the cycle length
to be collected. In lines 20-23, the random variables for the up and
downtime are constructed using exponential distributions.
As show in the following code listing, the initialize() method sets up the component.The variable myTimeLastUp is set to 0.0 in order to assume that the last time the component was in the UP state started at time 0.0. Thus,
we are assuming that the component starts the simulation in the UP
state. Finally, in line 7 the initial event is scheduled to cause the
component to go down according to the uptime distribution. This is the
first event and then the component can start its regular up and down
pattern. In the action associated with the change to the UP state,
line 18 sets the state to UP. Line 22 schedules the time until the
component goes down. Line 16 causes statistics to be collected on the
value of the cycle length. The code getTime()-myTimeLastUp represents
the elapsed time since the value of myTimeLastUp was set (in line 20),
which represents the cycle length. The DownChangeAction is very similar.
Line 31 counts the number of failures (times that the component has gone
down). Line 32 sets the state of the component to DOWN and line 34
schedules when the component should next transition into the UP state.
public void initialize() {
// assume that the component starts in the UP state at time 0.0
myTimeLastUp = 0.0;
myState.setValue(UP);
// schedule the time that it goes down
scheduleEvent(myDownChangeAction, myUpTime.getValue());
//schedule(myDownChangeAction).name("Down").in(myUpTime).units();
}
private class UpChangeAction extends EventAction {
@Override
public void action(JSLEvent event) {
// this event action represents what happens when the component goes up
// record the cycle length, the time btw up states
myCycleLength.setValue(getTime() - myTimeLastUp);
// component has just gone up, change its state value
myState.setValue(UP);
// record the time it went up
myTimeLastUp = getTime();
// schedule the down state change after the uptime
scheduleEvent(myDownChangeAction, myUpTime.getValue());
}
}
private class DownChangeAction extends EventAction {
@Override
public void action(JSLEvent event) {
// component has just gone down, change its state value
myCountFailures.increment();
myState.setValue(DOWN);
// schedule when it goes up afer the down time
scheduleEvent(myUpChangeAction, myDownTime.getValue());
}
}The following listing presents the code to construct and execute the simulation. This code is very similar to previously presented code for running a simulation. In line 3, the simulation is constructed. Then, in line 5, the model associated with the simulation is accessed. This model is then used to construct an instance of the UpDownComponent in line 7. Finally, lines 9-15 represent getting a SimulationReporter, running the simulation, and causing output to be written to the console.
public static void main(String[] args) {
// create the simulation
Simulation s = new Simulation("UpDownComponent");
s.turnOnDefaultEventTraceReport();
s.turnOnLogReport();
// get the model associated with the simulation
Model m = s.getModel();
// create the model element and attach it to the model
UpDownComponent tv = new UpDownComponent(m);
// make the simulation reporter
SimulationReporter r = s.makeSimulationReporter();
// set the running parameters of the simulation
s.setNumberOfReplications(5);
s.setLengthOfReplication(5000.0);
// tell the simulation to run
s.run();
r.printAcrossReplicationSummaryStatistics();
}The results for the average time in the up state and the cycle length are consistent with the theoretically computed results.
---------------------------------------------------------
Across Replication Statistical Summary Report
Sat Dec 31 18:31:27 EST 2016
Simulation Results for Model: UpDownComponent_Model
Number of Replications: 30
Length of Warm up period: 0.0
Length of Replications: 5000.0
---------------------------------------------------------
Response Variables
---------------------------------------------------------
Name Average Std. Dev. Count
---------------------------------------------------------
state 0.335537 0.005846 30.000000
cycle length 2.994080 0.040394 30.000000
---------------------------------------------------------
---------------------------------------------------------
Counters
---------------------------------------------------------
Name Average Std. Dev. Count
---------------------------------------------------------
count failures 1670.066667 22.996152 30.000000
---------------------------------------------------------This example only scratches the surface of what is possible. Imagine if
there were 20 components. We could easily create 20 of instances and add
them to the model. Even more interesting would be to define the state of
the system based on which components were in the up state. This would be
the beginning of modeling the reliability of a complex system. This type
of modeling can be achieved by making the individual model elements
(e.g. UpDownComponent) more reusable and allow the modeling objects to
interact in complex ways. More complex modeling will be the focus of the
next chapter.
6.5.4 Modeling a Simple Queueing System
This example considers a small pharmacy that has a single line for waiting customers and only one pharmacist. Assume that customers arrive at a drive through pharmacy window according to a Poisson distribution with a mean of 10 per hour. The time that it takes the pharmacist to serve the customer is random and data has indicated that the time is well modeled with an exponential distribution with a mean of 3 minutes. Customers who arrive to the pharmacy are served in the order of arrival and enough space is available within the parking area of the adjacent grocery store to accommodate any waiting customers.
Figure 6.8: Drive Through Pharmacy
The drive through pharmacy system can be conceptualized as a single server waiting line system, where the server is the pharmacist. An idealized representation of this system is shown in Figure 6.8. If the pharmacist is busy serving a customer, then additional customers will wait in line. In such a situation, management might be interested in how long customers wait in line, before being served by the pharmacist. In addition, management might want to predict if the number of waiting cars will be large. Finally, they might want to estimate the utilization of the pharmacist in order to ensure that he or she is not too busy.
When modeling the system first question to ask is: What is the system? In this situation, the system is the pharmacist and the potential customers as idealized in Figure 6.8. Now you should consider the entities of the system. An entity is a conceptual thing of importance that flows through a system potentially using the resources of the system. Therefore, one of the first questions to ask when developing a model is: What are the entities? In this situation, the entities are the customers that need to use the pharmacy. This is because customers are discrete things that enter the system, flow through the system, and then depart the system.
Since entities often use things as they flow through the system, a natural question is to ask: What are the resources that are used by the entities? A resource is something that is used by the entities and that may constrain the flow of the entities within the system. Another way to think of resources is to think of the things that provide service in the system. In this situation, the entities “use” the pharmacist in order to get their medicine. Thus, the pharmacist is a resource.
Another useful conceptual modeling tool is the activity diagram. An activity is an operation that takes time to complete. An activity is associated with the state of an object over an interval of time. Activities are defined by the occurrence of two events which represent the activity’s beginning time and ending time and mark the entrance and exit of the state associated with the activity. An activity diagram is a pictorial representation of the process (steps of activities) for an entity and its interaction with resources while within the system. If the entity is a temporary entity (i.e. it flows through the system) the activity diagram is called an activity flow diagram. If the entity is permanent (i.e. it remains in the system throughout its life) the activity diagram is called an activity cycle diagram. The notation of an activity diagram is very simple, and can be augmented as needed to explain additional concepts:
Queues: shown as a circle with queue labeled inside
Activities: shown as a rectangle with appropriate label inside
Resources: shown as small circles with resource labeled inside
Lines/arcs: indicating flow (precedence ordering) for engagement of entities in activities or for obtaining resources. Dotted lines are used to indicate the seizing and releasing of resources.
zigzag lines: indicate the creation or destruction of entities
Activity diagrams are especially useful for illustrating how entities interact with resources. In addition, activity diagrams help in finding the events and in identifying some the state changes that must be modeled. Activity diagrams are easy to build by hand and serve as a useful communication mechanism. Since they have a simple set of symbols, it is easy to use an activity diagram to communicate with people who have little simulation background. Activity diagrams are an excellent mechanism to document a conceptual model of the system before building the model.
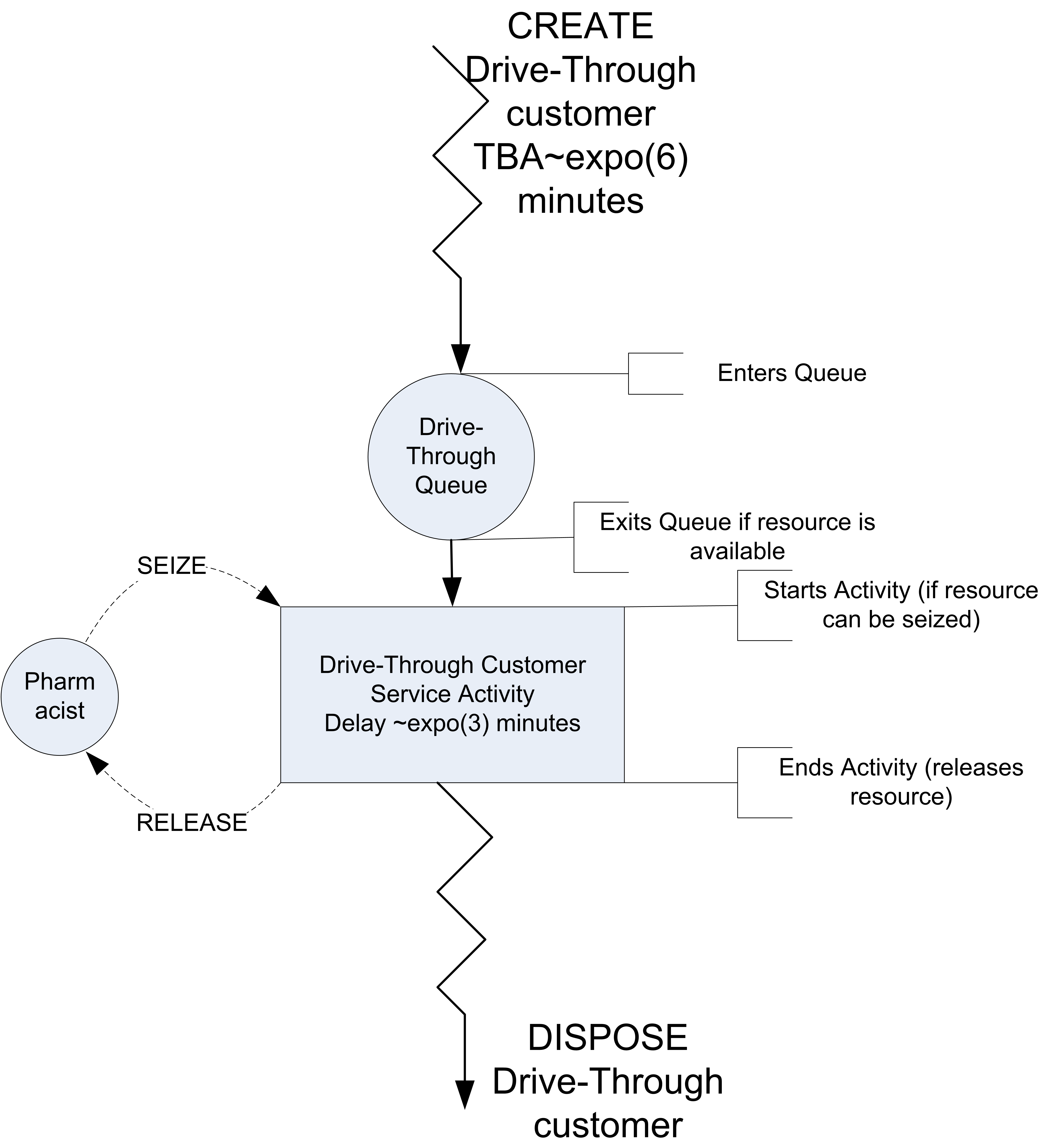
Figure 6.9: Activity Diagram of Drive through Pharmacy
Figure 6.9 shows the activity diagram for the pharmacy situation. The diagram describes the life of an entity within the system. The zigzag lines at the top of the diagram indicate the creation of an entity. Consider following the life of the customer through the pharmacy. Following the direction of the arrows, the customers are first created and then enter the queue. Notice that the diagram clearly shows that there is a queue for the drive-through customers. You should think of the entity flowing through the diagram. As it flows through the queue, the customer attempts to start an activity. In this case, the activity requires a resource. The pharmacist is shown as a resource (circle) next to the rectangle that represents the service activity.
The customer requires the resource in order to start its service activity. This is indicated by the dashed arrow from the pharmacist (resource) to the top of the service activity rectangle. If the customer does not get the resource, they wait in the queue. Once they receive the number of units of the resource requested, they proceed with the activity. The activity represents a delay of time and in this case the resource is used throughout the delay. After the activity is completed, the customer releases the pharmacist (resource). This is indicated by another dashed arrow, with the direction indicating that the units of the resource aare being put back or released. After the customer completes its service activity, the customer leaves the system. This is indicated with the zigzag lines going to no-where and indicating that the object leaves the system and is disposed The conceptual model of this system can be summarized as follows:
System: The system has a pharmacist that acts as a resource, customers that act as entities, and a queue to hold the waiting customers. The state of the system includes the number of customers in the system, in the queue, and in service.
Events: Arrivals of customers to the system, which occur within an inter-event time that is exponentially distributed with a mean of 6 minutes.
Activities: The service time of the customers are exponentially distributed with a mean of 3 minutes.
Conditional delays: A conditional delay occurs when an entity has to wait for a condition to occur in order to proceed. In this system, the customer may have to wait in a queue until the pharmacist becomes available.
With an activity diagram and pseudo-code such as this available to represent a solid conceptual understanding of the system, you can begin the model development process.
In the current example, pharmacy customers arrive according to a Poisson process with a mean of \(\lambda\) = 10 per hour. According to probability theory, this implies that the time between arrivals is exponentially distributed with a mean of (1/\(\lambda\)). Thus, for this situation, the mean time between arrivals is 6 minutes.
\[\frac{1}{\lambda} = \frac{\text{1 hour}}{\text{10 customers}} \times \frac{\text{60 minutes}}{\text{1 hour}} = \frac{\text{6 minutes}}{\text{customers}}\]
Let’s assume that the pharmacy is open 24 hours a day, 7 days a week. In other words, it is always open. In addition, assume that the arrival process does not vary with respect to time. Finally, assume that management is interested in understanding the long term behavior of this system in terms of the average waiting time of customers, the average number of customers, and the utilization of the pharmacist.
To simulate this situation over time, you must specify how long to run the model. Ideally, since management is interested in long run performance, you should run the model for an infinite amount of time to get long term performance; however, you probably don’t want to wait that long! For the sake of simplicity, assume that 10,000 hours of operation is long enough.
The logic of this model follows very closely the discussion of the bank teller example. Let’s define the following variable:
- Let \(t\) represent the current simulation clock time.
- Let \(c\) represent the number of available pharmacists
- Let \(N(t)\) represent the number of customers in the system at any time \(t\).
- Let \(Q(t)\) represent the number of customers waiting in line for the at any time \(t\).
- Let \(B(t)\) represent the number of pharmacists that are busy at any time \(t\).
- Let \(TBA_i\) represent the time between arrivals, which we will assume is exponentially distributed with a mean of 6 minutes.
- Let \(ST_i\) represent the service time of the \(i^{th}\) customer, which we will assume is exponentially distributed with a mean of 3 minutes.
- Let \(E_a\) represent the arrival event.
- Let \(E_s\) represent the end of service event.
- Let \(K\) represent the number of customers processed
Within the JSL model, we will model \(N(t)\), \(Q(t)\), and \(B(t)\) with instances of the TimeWeighted class The use of the TimeWeighted class will automate the collection of time averages for these variables as discussed in Section 6.4. Both \(TBA_i\) and \(ST_i\) will be modeled with instances of the RandomVariable class instantiated with instances of the ExponentialRV class. The pseudo-code for this situation is as follows.
Arrival Actions for Event \(E_a\)
N(t) = N(t) + 1
if (B(t) < c)
B(t) = B(t) + 1
schedule E_s at time t + ST_i
else
Q(t) = Q(t) + 1
endif
schedule E_a at time t + TBA_iIn the arrival actions, first we increment the number of customers in the system. Then, the number of busy pharmacists is compared to the number of pharmacists that are available. If there is an available pharmacist, the number of busy pharmacists is incremented and the end of service for the arriving customer is scheduled. If all the pharmacists are busy, then the customer must wait in the queue, which is indicated by incrementing the number in the queue. To continue the arrival process, the arrival of the next customer is scheduled.
End of Service Actions for Event \(E_s\)
B(t) = B(t) - 1
if (Q(t) > 0)
Q(t) = Q(t) - 1
B(t) = B(t) + 1
schedule E_s at time t + ST_i
endif
N(t) = N(t) - 1
K = K + 1In the end of service actions, the number of busy pharmacists is decreased by one because the pharmacist has completed service for the departing customer. Then the queue is checked to see if it has customers. If the queue has customers, then a customer is removed from the queue (decreasing the number in queue) and the number of busy pharmacists is increased by one. In addition, the end of service event is scheduled. Finally, the number of customers in the system is decremented and the count of the total customers processes is incremented.
The following code listing presents the definition of the variables and their creation within Java. The drive through pharmacy system is modeled via a class DriveThroughPharmacy that sub-classes from SchedulingElement to provide the ability to schedule events. The RandomVariable instances myServiceRV and myArrivalRV are used to represent the \(ST_i\) and \(TBA_i\) random variables. \(B(t)\), \(N(t)\), and \(Q(t)\) are modeled with the objects myNumBusy, myNS, and myQ, respectively, all instances of the TimeWeighted class. The tabulation of the number of processed customers, \(K\), is modeled with a JSL counter, using the Counter class.
public class DriveThroughPharmacy extends SchedulingElement {
private int myNumPharmacists;
private final RandomVariable myServiceRV;
private final RandomVariable myArrivalRV;
private final TimeWeighted myNumBusy;
private final TimeWeighted myNS;
private final TimeWeighted myQ;
private final ArrivalEventAction myArrivalEventAction;
private final EndServiceEventAction myEndServiceEventAction;
private final Counter myNumCustomers;
public DriveThroughPharmacy(ModelElement parent) {
this(parent, 1,
new ExponentialRV(1.0), new ExponentialRV(0.5));
}
public DriveThroughPharmacy(ModelElement parent, int numPharmacists) {
this(parent, numPharmacists, new ExponentialRV(1.0), new ExponentialRV(0.5));
}
public DriveThroughPharmacy(ModelElement parent, int numPharmacists,
RandomIfc timeBtwArrivals, RandomIfc serviceTime) {
super(parent);
Objects.requireNonNull(timeBtwArrivals, "The time between arrivals must not be null");
Objects.requireNonNull(serviceTime, "The service time must not be null");
if (numPharmacists <= 0){
throw new IllegalArgumentException("The number of pharmacists must be >= 1");
}
myNumPharmacists = numPharmacists;
myArrivalRV = new RandomVariable(this, timeBtwArrivals, "Arrival RV");
myServiceRV = new RandomVariable(this, serviceTime, "Service RV");
myQ = new TimeWeighted(this, "PharmacyQ");
myNumBusy = new TimeWeighted(this, 0.0, "NumBusy");
myNS = new TimeWeighted(this, 0.0, "# in System");
myNumCustomers = new Counter(this, "Num Served");
myArrivalEventAction = new ArrivalEventAction();
myEndServiceEventAction = new EndServiceEventAction();
}The main constructor of the DriveThroughPharmacy class checks for valid input parameters, instantiates the JSL model elements, and instantiates the arrival and end of service event actions. Notice how the other constructors call the main constructor with default arguments.
As can be seen in the following Java code, the arrival event is represented by the inner class ArrivalEventAction extending the abstract class EventAction to model the arrival event action. The Java code closely follows the pseudo-code. Notice the use of the initialize() method to schedule the first arrival event. The initialize() method is called just prior to the start of the replication for the simulation. The modeler can think of the initialize() method as being called at time \(t^{-}=0\).
protected void initialize() {
super.initialize();
// start the arrivals
scheduleEvent(myArrivalEventAction, myArrivalRV);
}
private class ArrivalEventAction extends EventAction {
@Override
public void action(JSLEvent event) {
myNS.increment(); // new customer arrived
if (myNumBusy.getValue() < myNumPharmacists) { // server available
myNumBusy.increment(); // make server busy
// schedule end of service
scheduleEvent(myEndServiceEventAction, myServiceRV);
} else {
myQ.increment(); // customer must wait
}
// always schedule the next arrival
scheduleEvent(myArrivalEventAction, myArrivalRV);
}
}In line 4 the first arrival event is scheduled
within the initialize() method. Within the ArrivalEventAction class implementation of
the action() method, we see the number of customers in the system incremented, the status of the pharmacists checked, and customers either starting service or having to wait in the queue.
The following code fragment presents the logic associated with the end of service event.
private class EndServiceEventAction extends EventAction {
@Override
public void action(JSLEvent event) {
myNumBusy.decrement(); // customer is leaving server is freed
if (myQ.getValue() > 0) { // queue is not empty
myQ.decrement();//remove the next customer
myNumBusy.increment(); // make server busy
// schedule end of service
scheduleEvent(myEndServiceEventAction, myServiceRV);
}
myNS.decrement(); // customer left system
myNumCustomers.increment();
}
}First the number of busy servers is decremented
because a pharmacist is becoming idle. Then, the queue is
checked to see if it is not empty. If the queue is not empty, then the
next customer must be removed, the server made busy again
and the customer scheduled into service. Finally, the TimeWeighted variable,
myNS, indicates that a customer has departed the system and the Counter for the number of customers processed is incremented.
The following method can be used to run the model based on a desired number of servers.
public static void runModel(int numServers) {
Simulation sim = new Simulation("Drive Through Pharmacy");
sim.setNumberOfReplications(30);
sim.setLengthOfReplication(20000.0);
sim.setLengthOfWarmUp(5000.0);
// add DriveThroughPharmacy to the main model
DriveThroughPharmacy dtp = new DriveThroughPharmacy(sim.getModel(), numServers);
dtp.setArrivalRS(new ExponentialRV(6.0));
dtp.setServiceRS(new ExponentialRV(3.0));
sim.run();
sim.printHalfWidthSummaryReport();
}The reports indicate that the utilization of the pharmacist is about 50%. This means that about 50% of the time the pharmacist was busy. For this type of system, this is probably not a bad utilization, considering that the pharmacist probably has other in-store duties. The reports also indicate that there was less than one customer on average waiting for service.
Half-Width Statistical Summary Report - Confidence Level (95.000)%
Name Count Average Half-Width
-----------------------------------------------------------------------
PharmacyQ 30 0.4976 0.0270
NumBusy 30 0.4994 0.0055
# in System 30 0.9971 0.0316
Num Served 30 2507.6333 20.5291
-----------------------------------------------------------------------This single server waiting line system is a very common situation in practice. In fact, this exact situation has been studied mathematically through a branch of operations research called queuing theory. For specific modeling situations, formulas for the long term performance of queuing systems can be derived. This particular pharmacy model happens to be an example of an M/M/1 queuing model. The first M stands for Markov arrivals, the second M stands for Markov service times, and the 1 represents a single server. Markov was a famous mathematician who examined the exponential distribution and its properties. According to queuing theory, the expected number of customer in queue, \(L_q\), for the M/M/1 model is:
\[ \begin{aligned} \label{ch4:eq:mm1} L_q & = \dfrac{\rho^2}{1 - \rho} \\ \rho & = \lambda/\mu \\ \lambda & = \text{arrival rate to queue} \\ \mu & = \text{service rate} \end{aligned} \]
In addition, the expected waiting time in queue is given by \(W_q = L_q/\lambda\). In the pharmacy model, \(\lambda\) = 1/6, i.e. 1 customer every 6 minutes on average, and \(\mu\) = 1/3, i.e. 1 customer every 3 minutes on average. The quantity, \(\rho\), is called the utilization of the server. Using these values in the formulas for \(L_q\) and \(W_q\) results in:
\[\begin{aligned} \rho & = 0.5 \\ L_q & = \dfrac{0.5 \times 0.5}{1 - 0.5} = 0.5 \\ W_q & = \dfrac{0.5}{1/6} = 3 \: \text{minutes}\end{aligned}\]
In comparing these analytical results with the simulation results, you can see that they match to within statistical error. The appendix presents an analytical treatment of queues. These analytical results are available for this special case because the arrival and service distributions are exponential; however, simple analytical results are not available for many common distributions, e.g. lognormal. With simulation, you can easily estimate the above quantities as well as many other performance measures of interest for wide ranging queuing situations. For example, through simulation you can easily estimate the chance that there are 3 or more cars waiting.