8.3 Analysis of Finite Horizon Simulations
This section illustrates how tally-based and time-persistent statistics are collected within a replication and how statistics are collected across replications. Finite horizon simulations can be analyzed by traditional statistical methodologies that assume a random sample, i.e. independent and identically distributed random variables. A simulation experiment is the collection of experimental design points (specific input parameter values) over which the behavior of the model is observed. For a particular design point, you may want to repeat the execution of the simulation multiple times to form a sample at that design point. To get a random sample, you execute the simulation starting from the same initial conditions and ensure that the random numbers used within each replication are independent. Each replication must also be terminated by the same conditions. It is very important to understand that independence is achieved across replications, i.e. the replications are independent. The data within a replication may or may not be independent.
The method of independent replications is used to analyze finite horizon simulations. Suppose that \(n\) replications of a simulation are available where each replication is terminated by some event \(E\) and begun with the same initial conditions. Let \(Y_{rj}\) be the \(j^{th}\) observation on replication \(r\) for \(j = 1,2,\cdots,m_r\) where \(m_r\) is the number of observations in the \(r^{th}\) replication, and \(r = 1,2,\cdots,n\), and define the sample average for each replication to be:
\[\bar{Y}_r = \frac{1}{m_r} \sum_{j=1}^{m_r} Y_{rj}\]
If the data are time-based then,
\[\bar{Y}_r = \frac{1}{T_E} \int_0^{T_E} Y_r(t) \mathrm{d}t\]
\(\bar{Y}_r\) is the sample average based on the observation within the \(r^{th}\) replication. It is a random variable that can be observed at the end of each replication, therefore, \(\bar{Y}_r\) for \(r = 1,2,\ldots,n\) forms a random sample. Thus, standard statistical analysis of the random sample can be performed.
To make this concrete, suppose that you are examining a bank that opens with no customers at 9 am and closes its doors at 5 pm to prevent further customers from entering. Let, \(W_{rj} j = 1,\ldots,m_r\), represents the sequence of waiting times for the customers that entered the bank between 9 am and 5 pm on day (replication) \(r\) where \(m_r\) is the number of customers who were served between 9 am and 5 pm on day \(r\). For simplicity, ignore the customers who entered before 5 pm but did not get served until after 5 pm. Let \(N_r (t)\) be the number of customers in the system at time \(t\) for day (replication) \(r\). Suppose that you are interested in the mean daily customer waiting time and the mean number of customers in the bank on any given 9 am to 5 pm day, i.e. you are interested in \(E[W_r]\) and \(E[N_r]\) for any given day. At the end of each replication, the following can be computed:
\[\bar{W}_r = \frac{1}{m_r} \sum_{j=1}^{m_r} W_{rj}\]
\[\bar{N}_r = \dfrac{1}{8}\int_0^8 N_r(t)\ \mathrm{d}t\]
At the end of all replications, random samples: \(\bar{W}_r\) and \(\bar{N}_r\) are available from which sample averages, standard deviations, confidence intervals, etc. can be computed. Both of these samples are based on observations of within replication data.
Both \(\bar{W_r}\) and \(\bar{N_r}\) for \(r = 1,2,\ldots,n\) are averages of many observations within the replication. Sometimes, there may only be one observation based on the entire replication. For example, suppose that you are interested in the probability that someone is still in the bank when the doors close at 5 pm, i.e. you are interested in \(\theta = Pr\{N(t = 5 pm) > 0\}\). In order to estimate this probability, an indicator variable can be defined within the simulation and observed each time the condition was met or not. For this situation, an indicator variable,\(I_r\), for each replication can be defined as follows:
\[ I_r = \begin{cases} 1 & N(t = 5 pm) > 0\\ 0 & N(t = 5 pm) \leq 0 \\ \end{cases} \]
Therefore, at the end of the replication, the simulation must tabulate whether or not there are customers in the bank and record the value of this indicator variable. Since this happens only once per replication, a random sample of the \(I_r\) for \(r = 1,2,\ldots,n\) will be available after all replications have been executed. We can use the observations of the indicator variable to estimate the desired probability.
Since the analysis of the system will be based on a random sample, the key design criteria for the experiment will be the required number of replications. In other words, you need to determine the sample size.
Because confidence intervals may form the basis for decision making, you can use the confidence interval half-width in determining the sample size. For example, in estimating \(E[W_r]\) for the bank example, you might want to be 95% confident that you have estimated the true waiting time to within \(\pm 2\) minutes.
There are three related methods that are commonly used for determining the sample size for this situation:
an iterative method based on the t-distribution,
an approximate method based on the normal distribution, and
the half-width ratio method
Each of these methods assumes that the observations in the sample are independent and identically distributed from a normal distribution. In addition, the methods also assume that the pilot replications are representative of the population under study. When the data are not normally distributed, you must rely on the central limit theorem to get approximate results. The assumption of normality is typically justified when across replication statistics are based on within replication averages.
Determining the sample size for a simulation experiment has already been discussed in Section 5.2.2 of Chapter 5, the following section will illustrate the half-width ratio method for determining the number of replications because it is often seen in practice.
8.3.1 Determining the Number of Replications
As a reminder, we repeat some of the exposition from Section 5.2.2. If you make a pilot run of \(n_0\) replications you can use the half-width from the pilot run to determine how many replications you need to have to be close to a desired half-width bound in the full experiment. This is called the half-width ratio method.
Let \(h_0\) be the initial value for the half-width from the pilot run of \(n_0\) replications.
\[\begin{equation} h_0 = t_{\alpha/2, n_0 - 1} \dfrac{s_0}{\sqrt{n_0}} \tag{8.1} \end{equation}\]
Solving for \(n_0\) yields:
\[\begin{equation} n_0 = t_{\alpha/2, n_0 -1}^{2} \dfrac{s_{0}^{2}}{h_{0}^{2}} (\#eq:n_0c) \end{equation}\]
Similarly for any \(n\), we have:
\[\begin{equation} n = t_{\alpha/2, n-1}^{2} \dfrac{s^{2}}{h^{2}} \tag{8.2} \end{equation}\]
Taking the ratio of \(n_0\) to \(n\) using equations @ref(eq:n_0c) and ((8.2) and assuming that \(t_{\alpha/2, n-1}\) is approximately equal to \(t_{\alpha/2, n_0 - 1}\) and \(s^2\) is approximately equal to \(s_0^2\), yields,
\[\begin{equation} n \cong n_0 \dfrac{h_0^2}{h^2} = n_0 \left(\frac{h_0}{h}\right)^2 \tag{8.3} \end{equation}\]
Equation (8.3) is the half-width ratio equation.
Now, let’s look at an example. Suppose a pilot run of a simulation model estimated that the average waiting time for a customer during the day was 11.485 minutes based on an initial sample size of 15 replications with a 95% confidence interval half-width of 1.04. Using the three sample size determination techniques, recommend a sample size to be 95% confident that you are within \(\pm 0.10\) of the true mean waiting time in the queue.
First we will do the half-width ratio method. We have that \(h_0 = 1.04\), \(n_0 = 15\), and \(h = 0.1\), thus:
\[n \cong n_0 \left(\frac{h_0}{h}\right)^2 = 15 \left(\frac{1.04}{0.1}\right)^2 = 1622.4 \cong 1623\]
To estimate a sample size based on the normal approximation method, we need to have the estimate of the initial sample standard deviation. Unfortunately, this is not directly reported, but it can be computed using Equation (8.1). Rearranging Equation (8.1) to solve for \(s_0\), yields:
\[s_0 = \dfrac{h_0\sqrt{n_0}}{t_{\alpha/2, n_0 - 1}}\]
Since we have a 95% confidence interval with \(n_0 = 15\), we have that \(t_{0.025, 14} = 2.145\), which yields,
\[s_0 = \dfrac{h_0\sqrt{n_0}}{t_{\alpha/2, n_0 - 1}} = \dfrac{1.04\sqrt{15}}{2.145} = 1.87781\]
Now, we can use the normal approximation method. By using \(h\) as the desired bound \(E\) and \(z_{0.025} = 1.96\), we have,
\[n \geq \biggl(\dfrac{z_{\alpha/2} s}{E}\biggr)^2 = \biggl(\dfrac{1.96 \times 1.87781}{0.1}\biggr)^2 = 1354.54 \approx 1355\]
The final method is to use the iterative method based on the following equation:
\[h = t_{\alpha/2, n-1} \dfrac{s}{\sqrt{n}} \leq E\]
This can be accomplished easily within a spreadsheet yielding \(n=1349\).
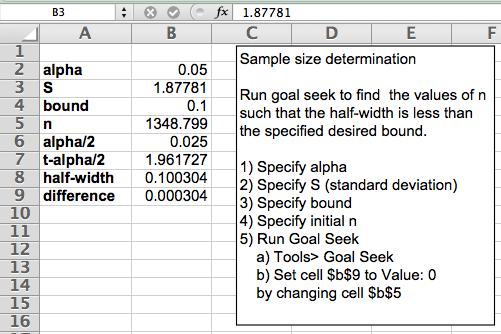
Figure 8.2: Iterative Method for Sample Size via Goal Seek
The three methods resulted in following recommendations:
an iterative method based on the t-distribution, n = 1349
an approximate method based on the normal distribution, n = 1355
the half-width ratio method, n = 1623
As noted in the discussion, the half-width ratio method recommended the largest number of replications.
In the case of an indicator variable such as, \(I_r\), which was suggested for use in estimating the probability that there are customers in the bank after 5 pm, the sampled observations are clearly not normally distributed. In this case, since you are estimating a proportion, you can use the sample size determination techniques for estimating proportions via equations (5.9) and (5.10).