8.4 Finite Horizon Example
This section presents a fictitious system involving the production of rings. The example illustrates how to collect tally based statistics, time based statistics, and statistics that can only be collected at the end of a replication. The analysis of a finite horizon simulation will be illustrated. In addition, the system also represents another example of how to use the station package.
Every morning the sales force at LOTR Makers, Inc. makes a number of confirmation calls to customers who have previously been visited by the sales force. They have tracked the success rate of their confirmation calls over time and have determined that the chance of success varies from day to day. They have modeled the probability of success for a given day as a beta random variable with parameters \(\alpha_1 = 5\) and \(\alpha_2 = 1.5\) so that the mean success rate is about 77%. They always make 100 calls every morning. Each sales call will or will not result in an order for a pair of magical rings for that day. Thus, the number of pairs of rings to produce every day is a binomial random variable, with \(p\) determined by the success rate for the day and \(n = 100\) representing the total number of calls made. Note that \(p\) is random in this modeling.
The sales force is large enough and the time to make the confirmation calls small enough so as to be able to complete all the calls before releasing a production run for the day. In essence, ring production does not start until all the orders have been confirmed, but the actual number of ring pairs produced every day is unknown until the sales call confirmation process is completed. The time to make the calls is negligible when compared to the overall production time.
Besides being magical, one ring is smaller than the other ring so that the smaller ring must fit snuggly inside the larger ring. The pair of rings is produced by a master ring maker and takes uniformly between 5 to 15 minutes. The rings are then scrutinized by an inspector with the time (in minutes) being distributed according to a triangular distribution with parameters (2, 4, 7) for the minimum, the mode, and the maximum. The inspection determines whether the smaller ring is too big or too small when fit inside the bigger outer ring. The inside diameter of the bigger ring, \(D_b\), is normally distributed with a mean of 1.5 cm and a standard deviation of 0.002. The outside diameter of the smaller ring, \(D_s\), is normally distributed with a mean of 1.49 and a standard deviation of 0.005. If \(D_s > D_b\), then the smaller ring will not fit in the bigger ring; however, if \(D_b - D_s > tol\), then the rings are considered too loose. The tolerance is currently set at 0.02 cm.
If there are no problems with the rings, the rings are sent to a packer for custom packaging for shipment. A time study of the packaging time indicates that it is distributed according to a log-normal distribution with a mean of 7 minutes and a standard deviation of 1 minute. If the inspection shows that there is a problem with the pair of rings they are sent to a rework craftsman. The minimum time that it takes to rework the pair of rings has been determined to be 5 minutes plus some random time that is distributed according to a Weibull distribution with a scale parameter of 15 and a shape parameter of 5. After the rework is completed, the pair of rings is sent to packaging.
Currently, the company runs two shifts of 480 minutes each. Time after the end of the second shift is considered overtime. Management is interested in investigating the following:
The daily production time.
The probability of overtime.
The average number of pairs of rings in both the ring making process and the ring inspection process.
The average time that it takes for a pair of rings to go through both the ring making process and the ring inspection process. In addition, a 95% confidence interval for the mean time to complete these processes to within \(\pm\) 20 minutes is desired.
8.4.1 Conceptualizing the Model
Now let’s proceed with the modeling of this situation. We start with answering the basic model building questions.
What is the system? What information is known by the system?
The system is the LOTR Makers, Inc. sales calls and ring production processes. The system starts every day with the initiation of sales calls and ends when the last pair of rings produced for the day is shipped. The system knows the following:
Sales call success probability distribution: \(p \sim beta(\alpha_1 = 5,\alpha_2 = 1.5)\)
Number of calls to be made every morning: \(n = 100\)
Distribution of time to make the pair of rings: \(U(5,15)\)
Distributions associated with the big and small ring diameters: N(\(\mu\) = 1.5, \(\sigma\) = 0.002) and N(\(\mu\) = 1.49, \(\sigma\) = 0.005), respectively
Distribution of ring-inspection time: triangular(2,4,7)
Distribution of packaging time: lognormal(\(\mu_{l}\) = 7,\(\sigma_{l}\) = 1)
Distribution of rework time, 5 + Weibull(scale =15, shape =3)
Length of a shift: 480 minutes
What are the entities? What information must be recorded for each entity?
Possible entities are the sales calls and the production job (pair of rings) for every successful sales call. For every pair of rings, the diameters must be known.
What are the resources that are used by the entities?
The sales calls do not use any resources. The production job uses a master craftsman, an inspector, and a packager. It might also use a rework craftsman.
What are the activities? What are the processes? What are the events associated with the processes and activities? Write out or draw sketches of the process.
There are two processes: sales order and production. An outline of the sales order process should look like this:
Start the day.
Determine the likelihood of calls being successful.
Make the calls.
Determine the total number of successful calls.
Start the production jobs.
Notice that the sales order process takes zero time and that it occurs at the beginning of each day. Thus, there appears to be an event that occurs at time 0.0, that determines the number of production jobs and sends them to production. This type of situation is best modeled using the initialize() method to make the orders to be placed into production. From the problem statement, the number of production jobs is a binomial random variable with \(n= 100\) and \(p \sim BETA(\alpha_1 = 5,\alpha_2 = 1.5)\).
The following listing shows the constructor for this model and the initialize() method.
public LOTR(ModelElement parent, String name) {
super(parent, name);
mySalesCallProb = new RandomVariable(this, new BetaRV(5.0, 1.5));
myMakeRingTimeRV = new RandomVariable(this, new UniformRV(5, 15));
mySmallRingODRV = new RandomVariable(this, new NormalRV(1.49, 0.005 * 0.005));
myBigRingIDRV = new RandomVariable(this, new NormalRV(1.5, 0.002 * 0.002));
myInspectTimeRV = new RandomVariable(this, new TriangularRV(2, 4, 7));
myPackingTimeRV = new RandomVariable(this, new LognormalRV(7, 1));
myReworkTimeRV = new RandomVariable(this, new ShiftedRV(5.0, new WeibullRV(3, 15)));
myRingMakingStation = new SingleQueueStation(this, myMakeRingTimeRV,
"RingMakingStation");
myInspectionStation = new SingleQueueStation(this, myInspectTimeRV,
"InspectStation");
myReworkStation = new SingleQueueStation(this, myReworkTimeRV,
"ReworkStation");
myPackagingStation = new SingleQueueStation(this, myPackingTimeRV,
"PackingStation");
myRingMakingStation.setNextReceiver(myInspectionStation);
myInspectionStation.setNextReceiver(new AfterInspection());
myReworkStation.setNextReceiver(myPackagingStation);
myPackagingStation.setNextReceiver(new Dispose());
mySystemTime = new ResponseVariable(this, "System Time");
myNumInSystem = new TimeWeighted(this, "Num in System");
myNumCompleted = new Counter(this, "Num Completed");
myProbTooBig = new ResponseVariable(this, "Prob too Big");
myProbTooSmall = new ResponseVariable(this, "Prob too Small");
myProbOT = new ResponseVariable(this, "Prob of Over Time");
myEndTime = new ResponseVariable(this, "Time to Make Orders");
myNumInRMandInspection = new TimeWeighted(this, "Num in RM and Inspection");
myTimeInRMandInspection = new ResponseVariable(this, "Time in RM and Inspection");
}
@Override
protected void initialize() {
super.initialize();
double p = mySalesCallProb.getValue();
int n = JSLRandom.rBinomial(p, myNumDailyCalls);
for (int i = 0; i < n; i++) {
myRingMakingStation.receive(new RingOrder());
myNumInSystem.increment();
myNumInRMandInspection.increment();
}
}The constructor makes the random variables that model the number of successful calls and the probability that a call is successful. Then, the initialize() method, which is automatically called at the beginning of a replication (essentially at time 0.0), uses the random variables to first determine the probability of a successful call and then determines the number of successful calls. Finally, a for-loop is used to make the orders (new RingOrder()) and send them into production at the ring making station. Also, the number of orders in the system and the number of orders at the ring making and inspection stations is incremented.
The following code listing illustrates the modeling of the orders within the system.
private class RingOrder extends QObject {
private double myBigRingID;
private double mySmallRingOuterD;
private double myGap;
private boolean myNeedsReworkFlag = false;
private boolean myTooBigFlag = false;
private boolean myTooSmallFlag = false;
public RingOrder() {
this(getTime(), null);
}
public RingOrder(double creationTime, String name) {
super(creationTime, name);
myBigRingID = myBigRingIDRV.getValue();
mySmallRingOuterD = mySmallRingODRV.getValue();
myGap = myBigRingID - mySmallRingOuterD;
if (mySmallRingOuterD > myBigRingID) {
myTooBigFlag = true;
myNeedsReworkFlag = true;
} else if (myGap > myRingTol) {
myTooSmallFlag = true;
myNeedsReworkFlag = true;
}
}
}A RingOrder represents an order for a pair of rings. RingOrder is an inner class of LOTR. This was done so that the RingOrder has easy access to the random variables defined within the LOTR class. The outer ring’s inner diameter and the inner ring’s outer diameter are modeled using attributes for the order. The values for these attributes are set using the random variables that were defined as instance variables of the LOTR class and instantiated within the LOTR class’s constructor. The size of the gap and whether or not the ring needs rework is also computed. The condition of the ring in terms of whether the gap is too big or too small is specified. Since the RingOrder class extends the QObject class it has the ability to be held by instances of the Queue class. Once the order for the rings is made it is passed into production.
An outline of the production process should be something like this:
Make the rings (determine sizes).
Inspect the rings.
If rings do not pass inspection, perform rework
Package rings and ship.
Notice that in the production of the rings there are a number of activities that take place during which various resources are used. This situation is very similar to the Tie-Dye T-Shirt example in that the rings move from ring making to inspection (possibly rework) and finally to packaging. Each of these areas can be modeled using the SingleQueueStation class. The events associated with this situation include arrival to ring making, departure from ring making, arrival to inspection, departure from inspection, arrvial to rework, departure from rework, arrival to packaging and departure from packaging. Since the departure from an upstream station also represents an arrival to the downstream station, the number of events needed to model this situation can be consolidated. As mentioned, the SingleQueueStation can be used to model this situation by connecting the stations together. The construction of the stations and their connection is illustrated in the constructor for the LOTR system. Notice that the setNextReceiver() methods are used to connect the ring making station to the inspection station and to have the rework station send work to the packaging station.
One conceptually challenging aspect of this model is the fact that the rings will probabilistically go to the rework station or the packaging station. To model this situation, an inner class called AfterInspection was designed that implements the ReceiveQObjectIfc interface. An instance of this class is provided as the receiver for the inspection station. Thus, after the inspection station is done, the order for the ring (in the form of a QObject) will be sent to this logic.
In the following listing, lines 4 and 5 finish out the collection of the number of orders in the ring making and inspection stations and the collection of the time spent within those stations. Then, starting in line 6, the order is checked if it needs rework and if so, the rework station is told to receive it; otherwise, the packaging station is told to receive it.
protected class AfterInspection implements ReceiveQObjectIfc {
@Override
public void receive(QObject qObj) {
myNumInRMandInspection.decrement();
myTimeInRMandInspection.setValue(getTime() - qObj.getCreateTime());
RingOrder order = (RingOrder) qObj;
if (order.myNeedsReworkFlag) {
myReworkStation.receive(order);
} else {
myPackagingStation.receive(order);
}
}
}
protected class Dispose implements ReceiveQObjectIfc {
@Override
public void receive(QObject qObj) {
// collect final statistics
RingOrder order = (RingOrder) qObj;
myNumInSystem.decrement();
mySystemTime.setValue(getTime() - order.getCreateTime());
myNumCompleted.increment();
myProbTooBig.setValue(order.myTooBigFlag);
myProbTooSmall.setValue(order.myTooSmallFlag);
}
}
@Override
protected void replicationEnded() {
super.replicationEnded();
myProbOT.setValue(getTime() > myOTLimit);
myEndTime.setValue(getTime());
}Similar to previous examples, the Dispose inner class collects statistics at the system level and on the orders as they depart the system. Besides the collection of the number orders in the ring making and inspection stations, management also desired the collection of the probability of over time and the time that the production run will be completed. The collection of the chance of over time depends on when all of the production are completed. The problem statement requests the estimation of the probability of overtime work. The sales order process determines the number of rings to produce. The production process continues until there are no more rings to produce for that day. The number of rings to produce is a binomial random variable as determined by the sales order confirmation process. Thus, there is no clear run length for this simulation.
In the JSL, a replication of a simulation can end based on three situations:
A scheduled run length
A terminating condition is met
No more events to process
Because the production for the day stops when all the rings are produced, the third situation applies for this model. The simulation will end automatically after all the rings are produced. In essence, a day’s worth of production is simulated. Because the number of rings to produce is random and it takes a random amount of time to make, inspect, rework, and package the rings, the time that the simulation will end is a random variable. If this time is less than 960 (the time of two shifts), there will not be any overtime. If this time is greater than 960, production will have lasted past two shifts and thus overtime will be necessary. To assess the chance that there is overtime, you need to record statistics on how often the end of the simulation is past 960.
Thus, the easiest way to observe the over time is to understand that a replication of the simulation will end when there are no more events to process. Just like in the case of the initialize() method being called at the start of a replication, the replicationEnded() method of all model elements will be called when the simulation replication ends. This provides for the opportunity to supply code that will be executed when the replication ends. Also note that the replicationEnded() method is called before any logic that might clear statistical quantities and that no additional events happen after the replication ends. Lines 3 and 4 of the replicationEnded() method implement the collection of the probability of over time and the time that the simulation ends. This is accomplished with instances of the ResponseVariable class, which were declared as instance variables of the LOTR class and instantiated within its constructor.
The method getTime() available on all model elements provides the current time of the simulation. Thus, when the simulation ends, The method getTime() will be the time that the simulation ended. In this case, it will represent the time that the last ring completed processing. To estimate the chance that there is overtime, we use a ResponseVariable to capture the time. Since this occurs one time for each replication, the number of observations of the over time will be equal to the number of replications.
Running the model results in the user defined statistics for the probability of overtime and the average time to produce the orders as shown in in the folloing table. The probability of overtime appears to be about 3%, but their is a lot of variation for these 30 replications. The average time to produce an order is about 770 minutes. While the average is under 960, there still appears to be a reasonable chance of overtime occurring. What do you think causes the overtime? Can you ecommend an alternative to reduce the likelihood of overtime?
| Response Name | \(\bar{x}\) | \(s\) |
|---|---|---|
| RingMakingStation:R:Util | 0.980777 | 0.007716 |
| RingMakingStation:R:BusyUnits | 0.980777 | 0.007716 |
| RingMakingStation:Q:Num In Q | 36.877643 | 7.949062 |
| RingMakingStation:Q:Time In Q | 374.334264 | 79.128277 |
| RingMakingStation:NS | 37.858420 | 7.952406 |
| InspectStation:R:Util | 0.426290 | 0.022779 |
| InspectStation:R:BusyUnits | 0.426290 | 0.022779 |
| InspectStation:Q:Num In Q | 0.001148 | 0.001260 |
| InspectStation:Q:Time In Q | 0.011508 | 0.012382 |
| InspectStation:NS | 0.427438 | 0.023260 |
| ReworkStation:R:Util | 0.127256 | 0.050377 |
| ReworkStation:R:BusyUnits | 0.127256 | 0.050377 |
| ReworkStation:Q:Num In Q | 0.003795 | 0.006096 |
| ReworkStation:Q:Time In Q | 0.493970 | 0.794616 |
| ReworkStation:NS | 0.131051 | 0.052790 |
| PackingStation:R:Util | 0.690843 | 0.033373 |
| PackingStation:R:BusyUnits | 0.690843 | 0.033373 |
| PackingStation:Q:Num In Q | 0.108125 | 0.043984 |
| PackingStation:Q:Time In Q | 1.087263 | 0.411139 |
| PackingStation:NS | 0.798968 | 0.071767 |
| System Time | 398.068177 | 79.425695 |
| Num in System | 39.215877 | 7.992176 |
| Prob too Big | 0.026853 | 0.019754 |
| Prob too Small | 0.041889 | 0.019552 |
| Prob of Over Time | 0.033333 | 0.182574 |
| Time to Make Orders | 770.286991 | 159.076748 |
| Num in RM and Inspection | 38.285858 | 7.954368 |
| Time in RM and Inspection | 388.641522 | 79.155138 |
| Across Rep Stat Num Completed | 75.866667 | 15.904312 |
| Number of Replications 30 |
The final issue to be handled in this example is to specify the number of replications. Based on this initial run of 30 replication, the required number of replications will be computed to ensure a 95% confidence interval for the mean time to complete the ring making and inspection processes with an error bound of \(\pm\) 20 minutes. The estimated standard deviation for this time was 79.155138.
Using the normal approximation with \(\alpha = 0.05\), \(n_0\) = 30, \(s_0\) = 79.155138, and \(E = 20\), indicates that approximately \(n = 61\) replications are needed to meet the criteria.
\[ n \geq \biggl(\dfrac{z_{\alpha/2} s_0}{E}\biggr)^2 = \biggl(\dfrac{1.96 \times 79.155138}{20}\biggr)^2 \approx 61 \]
If you wanted to use the iterative method, you must first determine the standard deviation from the pilot replications. In the case of multiple replications, you can use the half-width value and equation ((8.1)) to compute \(s_0\).
Rerunning the simulation with \(n = 61\), yields a half-width of 20.77, which is very close to the criteria of 20. Note that the make and inspection time is highly variable. The methods to determine the half-width assume that the standard deviation, \(s_0\), in the pilot runs will be similar to the standard deviation observed in the final set of replications. However, when the full set of replications is run, the actual standard deviation may be different than used in the pilot run. Thus, the half-width criterion might not be exactly met. If the assumptions are reasonably met, there will be a high likelihood that the desired half-width will be very close to the desired criteria, as show in this example.
8.4.2 Sequential Sampling for Finite Horizon Simulations
The methods discussed for determining the sample size are based on pre-determining a fixed sample size and then making the replications. If the half-width equation is considered as an iterative function of \(n\):
\[h(n) = t_{\alpha/2, n - 1} \dfrac{s(n)}{\sqrt{n}} \leq E\]
Then, it becomes apparent that additional replications of the simulation can be executed until the desired half-with bound is met. This is called sequential sampling, and in this case the sample size of the experiment is not known in advance. The brute force method for implementing this approach would be to run and rerun the simulation each time increasing the number of replications until the criterion is met.
To implement this within the JSL, we need a way to stop or end a
simulation when a criteria or condition is met. Because of the
hierarchical nature of the model elements within a model and because
there are common actions that occur when running a model the Observer
pattern can be used here.
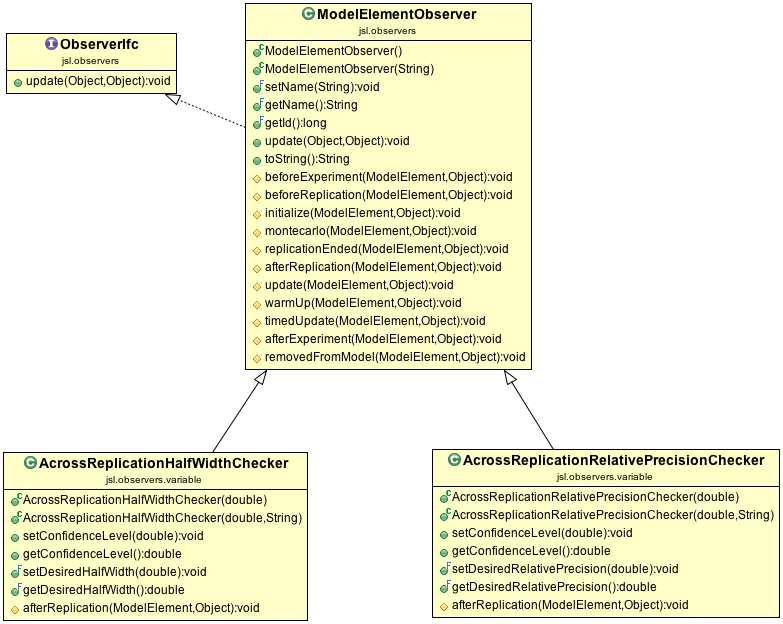
Figure 8.3: Half-Width Observer Checking Code
Figure 8.3 presents part of the
jsl.observers.variable package which defines a base class called
ModelElementObserver that can be attached to instances of ModelElement
and then will be notified if various actions take place. There are a
number of actions associated with a ModelElement that occur during a
simulation that can be listened for by a ModelElementObserver:
beforeExperiment()- This occurs prior to the first replication and before any events are executed.beforeReplication()- This occurs prior to each replication and before any events are executed. The event calendar is cleared after this action.initialize()- This occurs at the start of every replication (after beforeReplication() and after the event calendar is cleared) but before any events are executed. As we have seen, it is safe to schedule events in this method.warmUp()- This occurs during a replication if a warm up period has been specified for the model. The statistical accumulators are cleared during this action if applicable.replicationEnded()- This occurs at the end of every replication prior to the clearing of any statistical accumulators.afterReplication()- This occurs at the end of every replication after the statistical accumulators have been cleared for the replication.afterExperiment()- This occurs after all replications have been executed and prior to the end of the simulation.
ModelElementObservers are notified right after the ModelElement
experiences the above mentioned actions. Thus, users of the
ModelElementObserver need to understand that the state of the model
element is available after the simulation actions of the model element
have occurred.
The AcrossReplicationHalfWidthChecker class listens to the
afterReplication() method of a ResponseVariable and checks the current
value of the half-width. This is illustrated in the following code listing.
protected void afterReplication(ModelElement m, Object arg) {
ResponseVariable x = (ResponseVariable) m;
Simulation s = x.getSimulation();
if (s == null) {
return;
}
if (s.getCurrentReplicationNumber() <= 2.0) {
return;
}
StatisticAccessorIfc stat = x.getAcrossReplicationStatistic();
double hw = stat.getHalfWidth(getConfidenceLevel());
if (hw <= myDesiredHalfWidth) {
s.end("Half-width condition met for " + x.getName());
}
}Notice that a reference to the
observed ResponseVariable is used to get access to the across
replication statistics. If there are more than 2 replications, then the
half-width is checked against a user supplied desired half-width. If the
half-width criterion is met, then the simulation is told to end using
the Simulation class’s end() method. The end() method causes the simulation to
not execute any future replications and to halt further execution.
The following code listing illustrates how to set up half-width checking.
Simulation sim = new Simulation("LOTR Example");
// get the model
Model m = sim.getModel();
// add system to the main model
LOTR system = new LOTR(m, "LOTR");
ResponseVariable rsv = m.getResponseVariable("Time in RM and Inspection");
AcrossReplicationHalfWidthChecker hwc = new AcrossReplicationHalfWidthChecker(20.0);
rsv.addObserver(hwc);
// set the parameters of the experiment
sim.setNumberOfReplications(1000);
System.out.println("Simulation started.");
sim.run();
System.out.println("Simulation completed.");
sim.printHalfWidthSummaryReport();All that is needed is to get a reference to the response variable that needs to be check so that the observer can be attached. This can be done easily in the location of the code where the response variable is created or as in this example, the name of the response variable is used to get the reference from the model. Line 6 of the listing illustrates using the name to get the reference, followed by the construction of the checker (line 7) and attaching it as an observer (line 8).
In the sequential sampling experiment there were 66 replications. This is actually more than the recommended 61 replications for the fixed half-width method. This is perfectly possible, and emphasizes the fact that in the sequential sampling method, the number of replications is actually a random variable. If you were to use different streams and re-run the sequential sampling experiment, the number of replications completed may be different each time.
| Response Name | \(\bar{x}\) | \(hw\) |
|---|---|---|
| RingMakingStation:R:Util | 0.981083 | 0.002039 |
| RingMakingStation:R:BusyUnits | 0.981083 | 0.002039 |
| RingMakingStation:Q:Num In Q | 37.364044 | 1.963297 |
| RingMakingStation:Q:Time In Q | 380.608370 | 19.903070 |
| RingMakingStation:NS | 38.345127 | 1.964300 |
| InspectStation:R:Util | 0.426379 | 0.005022 |
| InspectStation:R:BusyUnits | 0.426379 | 0.005022 |
| InspectStation:Q:Num In Q | 0.000948 | 0.000263 |
| InspectStation:Q:Time In Q | 0.009558 | 0.002622 |
| InspectStation:NS | 0.427327 | 0.005109 |
| ReworkStation:R:Util | 0.127123 | 0.011491 |
| ReworkStation:R:BusyUnits | 0.127123 | 0.011491 |
| ReworkStation:Q:Num In Q | 0.004093 | 0.001949 |
| ReworkStation:Q:Time In Q | 0.530734 | 0.255424 |
| ReworkStation:NS | 0.131216 | 0.012288 |
| PackingStation:R:Util | 0.687782 | 0.006946 |
| PackingStation:R:BusyUnits | 0.687782 | 0.006946 |
| PackingStation:Q:Num In Q | 0.103600 | 0.008483 |
| PackingStation:Q:Time In Q | 1.050310 | 0.080851 |
| PackingStation:NS | 0.791382 | 0.013703 |
| System Time | 404.357533 | 19.948930 |
| Num in System | 39.695052 | 1.969934 |
| Prob too Big | 0.031764 | 0.004634 |
| Prob too Small | 0.038146 | 0.004449 |
| Prob of Over Time | 0.106061 | 0.076275 |
| Time to Make Orders | 782.451179 | 39.996433 |
| Num in RM and Inspection | 38.772454 | 1.964935 |
| Time in RM and Inspection | 394.965666 | 19.914630 |
| Across Rep Stat Num Completed | 76.803030 | 3.936414 |
| Number of replications: 66 |