7.6 Complex System Example
This section presents a more complex system that illustrates how to model entities that flow through a system and how to coordinate the flow. The example will reuse the single queue station modeling of previous examples; however, the entities (objects that flow in the system) require synchronization.
Suppose production orders for tie-dye T-shirts arrive to a production facility according to a Poisson process with a mean rate of 4 per hour. There are two basic psychedelic designs involving either red or blue dye. For some reason the blue shirts are a little more popular than the red shirts so that when an order arrives about 70% of the time it is for the blue dye designs. In addition, there are two different package sizes for the shirts, 3 and 5 units. There is a 25% chance that the order will be for a package size of 5 and a 75% chance that the order will be for a package size of 3. Each of the shirts must be individually hand made to the customer’s order design specifications. The time to produce a shirt (of either color) is uniformly distributed within the range of 3 to 5 minutes. There is currently one worker who is setup to make either shirt. When an order arrives to the facility, its type (red or blue) is determined and the pack size is determined. Then, the appropriate number of white (un-dyed) shirts are sent to the shirt makers with a note pinned to the shirt indicating the customer order, its basic design, and the pack size for the order. Meanwhile, the paperwork for the order is processed by a worker and a customized packaging letter and box is prepared to hold the order. It takes the paperwork worker between 8 to 10 minutes to make the box and print a custom thank you note. After the packaging is made the paperwork waits prior to final inspection for the shirts associated with the order. After the shirts are combined with the packaging, they are inspected by a packaging worker which is distributed according to a triangular distribution with a minimum of 5 minutes, a most likely value of 10 minutes, and a maximum value of 15 minutes. Finally, the boxed customer order is sent to shipping.
7.6.1 Conceptualizing the Model
Before proceeding you might want to jot down your answers to the following modeling recipe questions and then compare how you are doing with respect to what is presented in this section. The modeling recipe questions are:
What is the system? What information is known by the system?
What are the required performance measures?
What are the entities? What information must be recorded or remembered for each entity? How are entities introduced into the system?
What are the resources that are used by the entities? Which entities use which resources and how?
What are the process flows? Sketch the process or make an activity flow diagram
Develop pseudo-code for the situation
Implement the model
The entities can be conceptualized as the arriving orders. Since the shirts are processed individually, they should also be considered entities. In addition, the type of order (red or blue) and the size of the order (3 or 5) must be tracked. Since the type of the order and the size of the order are properties of the order, attributes can be used to model this information. The resources are the two shirt makers, the paperwork worker, and the packager. The flow is described in the scenario statement: orders arrive, shirts made, meanwhile packaging is made. Then, orders are assembled, inspected, and finally shipped. It should be clear that an EventGenerator, setup to generate Poisson arrivals can create the orders, but if shirts are entities, how should they be modeled and created? After this, there will be two types of entities in the model, the orders (paperwork) and the shirts. The shirts can be made and meanwhile the paperwork for the order can be processed. When the shirts for an order are made, they need to be combined together and associated with the order.
The activity diagram for this situation is given in Figure 7.8. After the order is created, the process separates into the order making process and the shirt making process. Notice that the orders and shirts must be synchronized together after each of these processes.
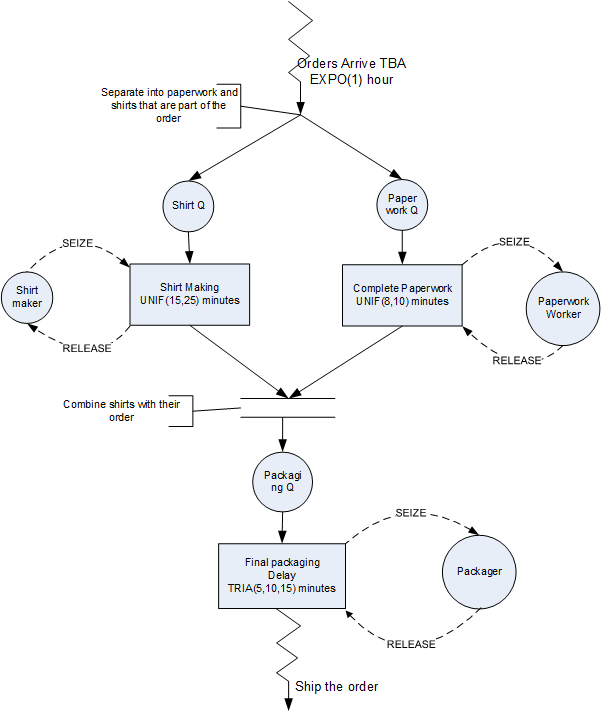
Figure 7.8: Activity Diagram for Tie Dye T-Shirts System
7.6.2 Implementing the Model
If it was not for the coordination between the orders
(paperwork/packaging) and the shirts in this system, the modeling would
be a straightforward application of concepts that have already been
presented. The processing of the shirts, the paperwork, and the final
packaging can all be modeled with instances of the SingleQueueStation
class, where the shirts go to one instance, the paperwork goes to
another instance, and the combined final order goes to the third
instance. Thus, if it was not for the fact that shirts must be combined
into an order and the order has to be combined with its paperwork before
packaging, the classes within the station package could handle this
modeling. In fact, the constructor for the implementation takes exactly
this approach as illustrated in the following code listing.
public TieDyeTShirts(ModelElement parent, String name) {
super(parent, name);
myTBOrders = new RandomVariable(this, new ExponentialRV(15));
myOrderGenerator = new EventGenerator(this, new OrderArrivals(),
myTBOrders, myTBOrders);
DEmpiricalRV type = new DEmpiricalRV(new double[]{1.0, 2.0}, new double[] {0.7, 1.0});
DEmpiricalRV size = new DEmpiricalRV(new double[]{3.0, 5.0}, new double[] {0.75, 1.0});
myOrderSize = new RandomVariable(this, size);
myOrderType = new RandomVariable(this, type);
myShirtMakingTime = new RandomVariable(this, new UniformRV(3, 5));
myPaperWorkTime = new RandomVariable(this, new UniformRV(8, 10));
myPackagingTime = new RandomVariable(this, new TriangularRV(5, 10, 15));
myShirtMakers = new SResource(this, 1, "ShirtMakers_R");
myPackager = new SResource(this, 1, "Packager_R");
myShirtMakingStation = new SingleQueueStation(this, myShirtMakers,
myShirtMakingTime, "Shirt_Station");
myWorker = new SResource(this, 1, "PW-Worker");
myPWStation = new SingleQueueStation(this, myWorker,
myPaperWorkTime, "PW_Station");
myPackagingStation = new SingleQueueStation(this, myPackager,
myPackagingTime, "Packing_Station");
// need to set senders/receivers
myShirtMakingStation.setNextReceiver(new AfterShirtMaking());
myPWStation.setNextReceiver(new AfterPaperWork());
myPackagingStation.setNextReceiver(new Dispose());
mySystemTime = new ResponseVariable(this, "System Time");
myNumInSystem = new TimeWeighted(this, "Num in System");
}In the constructor, lines 3 and 4, shows the
specification for the EventGenerator. Then, DEmpiricalRV random
variables are setup to model the order size and the order type, where 1
represents blue shirts and 2 represents red shirts. Lines 10-12 show the
modeling of the shirt making time, paperwork time, and packaging time
all using instances of the RandomVariable class. In lines 13-15 the
workers are modeled with instances of the SResource class, and in
lines 16-21, the SingleQueueStation class is used to model the use of
the resources and the activities for shirt making, paperwork, and
packaging. All that is left is connecting the stations together, which
is accomplished in lines 23-25 by setting the receivers for the
stations. The ‘magic’ of modeling the order coordination happens in the
receivers and how orders are modeled.
Before exploring that implementation, we can explore how orders enter and leave the system. The following listing presents how the orders are generated and how the orders leave the system.
private class OrderArrivals implements EventGeneratorActionIfc {
@Override
public void generate(EventGenerator generator, JSLEvent event) {
myNumInSystem.increment();
Order order = new Order();
List<Order.Shirt> shirts = order.getShirts();
for (Order.Shirt shirt : shirts) {
myShirtMakingStation.receive(shirt);
}
myPWStation.receive(order.getPaperWork());
}
}
protected class Dispose implements ReceiveQObjectIfc {
@Override
public void receive(QObject qObj) {
// collect final statistics
myNumInSystem.decrement();
mySystemTime.setValue(getTime() - qObj.getCreateTime());
Order o = (Order) qObj;
o.dispose();
}
}An implementation of an EventGeneratorListenerIfc interface called OrderArrivals is provided to
the EventGenerator. In line 5, the number of orders in the system is
incremented. Then, in line 6, a new order is made. The shirts associated
with the orders are then retrieved (line 7) and then sent to the shirt
making station (lines 9-11). Finally, line 12 retrieves the paperwork
from the order (order.getPaperWork()) and sends it to the paperwork
station. The implementation of the logic for orders to leave the system
is implemented in similar disposal logic as we have previously seen
(atarting at line 18). First, the number of orders is decremented and
the time that an order spent in the system collected. Then, the order is
disposed.
The modeling of the synchronization of the shirts and the paperwork
comes down to the following fact: when all the shirts are completed and
the paperwork is completed, then the order is completed and can be sent
to the packaging station. If the paperwork activity finishes before all
the shirts are completed, the order will be completed when the last
shirt is done. If all the shirts are completed before the paperwork is
completed, then the order waits until the paperwork is done. Thus, when
a shirt associated with an order is completed, we can check if the paper
work is done and if all shirts are done, the order can proceed. When the
paperwork is completed, we need to check if all shirts are done and if
so the order can proceed. Both shirt completion and paperwork completion
are events and these events are modeled within the SingleQueueStation
class. However, right after the events occur the SingleQueueStation
class uses its attached QObjectReceiverIfc instance. The logic for
checking for order completion can be added to the receivers. This logic
is presented in the following listing.
protected class AfterShirtMaking implements ReceiveQObjectIfc {
@Override
public void receive(QObject qObj) {
Order.Shirt shirt = (Order.Shirt) qObj;
shirt.setDoneFlag();
}
}
protected class AfterPaperWork implements ReceiveQObjectIfc {
@Override
public void receive(QObject qObj) {
Order.PaperWork pw = (Order.PaperWork) qObj;
pw.setDoneFlag();
}
}Because of how the Order class is implemented, this logic is not particularly interesting. As shown in the code listing, all that occurs is to indicate the the shirt is completed (line 6) and that the paperwork is completed (line 16). The Order class is implemented such that it is notified whenever a shirt is completed and when the paperwork is completed. If during this notification process, the entire order is completed, the order will be sent to the packaging station. This is the logic that we will explore next.
Because orders may need to wait, we are going to model them by
sub-classing from the QObject class. This allows the use of the Queue
class. In addition, shirts and paperwork are also entities that wait.
So, they will also be modeled as sub-classes of the QObject class.
Orders have a size and a type. In addition, orders contain shirts and
paperwork.The following listing shows the constructor and instance variables
for the Order class.
private class Order extends QObject {
private int myType;
private int mySize;
private PaperWork myPaperWork;
private List<Shirt> myShirts;
private int myNumCompleted;
private boolean myPaperWorkDone;
public Order(double creationTime, String name) {
super(creationTime, name);
myNumCompleted = 0;
myPaperWorkDone = false;
myType = (int) myOrderType.getValue();
mySize = (int) myOrderSize.getValue();
myShirts = new ArrayList<>();
for (int i = 1; i <= mySize; i++) {
myShirts.add(new Shirt());
}
myPaperWork = new PaperWork();
}The Order class is a private inner class of the
TieDyeTShirts class. This allows orders access to all the instance
variables and methods of the TieDyeTShirts class. It is declared private
since its usage is only within the TieDyeTShirts class. Order extends
QObject and has instance variables to represent the type and size of the
orders (lines 3 and 4). Lines 5 and 6 represent the associations between
the order and its shirts (held in a list) and its paperwork. In the
constructor body, the type and size are set from the random variables
declared in the TieDyeTShirts class. In addition, a list holding the
shirts is filled and the paperwork is created. The number of completed
shirts is noted as zero and the fact that the paperwork is not completed
is saved in an attribute.
The following listing illustrates the key methods associated with modeling the behavior of the orders.
public boolean isComplete() {
return ((areShirtsDone()) && (isPaperWorkDone()));
}
public boolean areShirtsDone() {
return (myNumCompleted == mySize);
}
public boolean isPaperWorkDone() {
return (myPaperWorkDone);
}
public int getNumShirtsCompleted() {
return myNumCompleted;
}
private void shirtCompleted() {
if (areShirtsDone()) {
throw new IllegalStateException("The order already has all its shirts.");
}
// okay not complete, need to add shirt
myNumCompleted = myNumCompleted + 1;
if (isComplete()) {
TieDyeTShirts.this.orderCompleted(this);
}
}
private void paperWorkCompleted() {
if (isPaperWorkDone()) {
throw new IllegalStateException("The order already has paperwork.");
}
myPaperWorkDone = true;
if (isComplete()) {
TieDyeTShirts.this.orderCompleted(this);
}
}The three methods, isCompleted(),
areShirtsDone(), and isPaperWorkDone()all check on the status of the
order. The two methods shirtCompleted() and paperWorkCompleted() are
used by shirts and paperwork to update the order’s state. The
shirtCompleted() method increments the number of shirts completed and if
the order is completed, the outer class, TieDyeTShirts is notified by
calling its orderCompleted() method. In addition, the
paperWorkCompleted() method does the same thing when it is completed.
These two methods are called by shirts and paperwork.
The following code presents the Shirt and PaperWork classes. The Shirt and PaperWork classes are inner classes of the Order class.
protected class Shirt extends QObject {
protected boolean myDoneFlag = false;
public Shirt() {
this(getTime());
}
public Shirt(double creationTime) {
this(creationTime, null);
}
public Shirt(double creationTime, String name) {
super(creationTime, name);
}
public Order getOrder() {
return Order.this;
}
public void setDoneFlag() {
if (myDoneFlag == true) {
throw new IllegalStateException("The shirt is already done.");
}
myDoneFlag = true;
Order.this.shirtCompleted();
}
public boolean isCompleted() {
return myDoneFlag;
}
}
protected class PaperWork extends Shirt {
@Override
public void setDoneFlag() {
if (myDoneFlag == true) {
throw new IllegalStateException("The paperwork is already done.");
}
myDoneFlag = true;
Order.this.paperWorkCompleted();
}
}
}The key methods are the setDoneFlag()methods in both classes. Notice that
when a shirt is completed the call Order.this.shirtCompleted() occurs.
Similar logic occurs within the PaperWork class. This is the
notification that they are completed so that the Order classs is
notified when they are completed.
7.6.3 Model Results
The following table presents the results of the simulation. From the utilization of the shirt making resource it is clear that more than one shirt maker is necessary.
| Response Name | \(\bar{x}\) | \(s\) |
|---|---|---|
| ShirtMakers_R:Util | 0.934393 | 0.009719 |
| ShirtMakers_R:BusyUnits | 0.934393 | 0.009719 |
| Packager_R:Util | 0.667315 | 0.006774 |
| Packager_R:BusyUnits | 0.667315 | 0.006774 |
| Shirt_Station:Q:NumInQ | 27.041158 | 7.192692 |
| Shirt_Station:Q:TimeInQ | 115.486332 | 29.686151 |
| Shirt_Station:NS | 27.975551 | 7.200011 |
| PW-Worker:Util | 0.600392 | 0.006394 |
| PW-Worker:BusyUnits | 0.600392 | 0.006394 |
| PW_Station:Q:NumInQ | 0.452418 | 0.020481 |
| PW_Station:Q:TimeInQ | 6.780610 | 0.256060 |
| PW_Station:NS | 1.052810 | 0.025685 |
| Packing_Station:Q:NumInQ | 0.015327 | 0.000827 |
| Packing_Station:Q:TimeInQ | 0.229741 | 0.011867 |
| Packing_Station:NS | 0.682642 | 0.007135 |
| System Time | 134.366279 | 29.657064 |
| Num in System | 8.982821 | 2.067345 |