7.3 Event Generators

A basic mechanism by which the occurrence of a patterned sequence of events is modeled is through the EventGenerator class. The EventGenerator class defines a repeating pattern for a sequence of events. The time between arrivals specifies an ordered sequence of events in time at which events are created and introduced to the model. At each event, the modeler can define the actions (state changes) that need to occur. The first event is governed by the specification of the time until the first event, which may be stochastic. The maximum number of events to occur in the sequence can be specified.

Figure 7.2 illustrates a compound arrival process where the time of the first arrival is given by T1, the time of the second arrival is given by T1 + T2, and the time of the third arrival is given by T1 + T2 + T3. In the figure, the number of arriving entities at each arriving event is given by N1, N2, and N3 respectively. The modeler can easily specify this type of arrival process using the EventGenerator class.

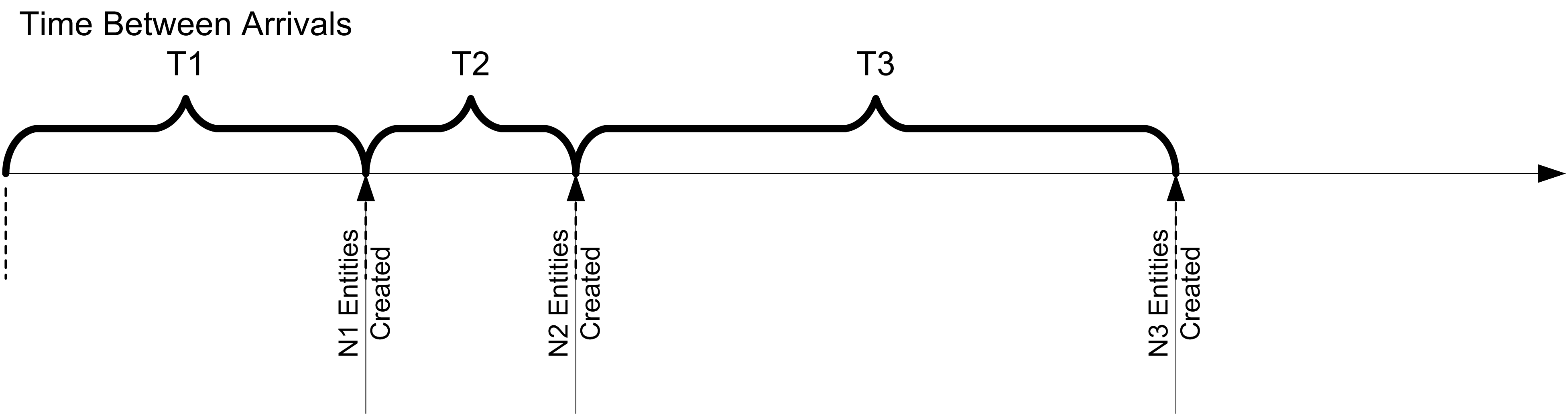
Figure 7.2: Example Arrival Process

For example, to specify a Poisson arrival process with mean rate \(\lambda\), an EventGenerator can be used. Why does this specify a Poisson arrival process? Because the time between arrivals for a Poisson process with rate \(\lambda\) is exponentially distributed with the mean of the exponential distribution being \(1/\lambda\). The the EventGenerator needs to have its time between arrival distribution specified as an exponential distribution with mean equal to \(1/\lambda\). To specify a compound arrival process, use a random variable to represent the number of occurrences per event. For example, suppose you have a compound Poisson process¹ where the distribution for the number created at each arrival is governed by a discrete distribution.

\[ P(X = x) = \begin{cases} 0.2 & \quad \text{x = 1}\\ 0.3 & \quad \text{x = 2}\\ 0.5 & \quad \text{x = 3} \end{cases} \]

The following code illustrates how to use an EventGenerator for this compound Poisson process with the number of arrivals specified with a discrete empirical random variable. Let’s go through this example before exploring the details of the EventGenerator class. In line 3 the EventGenerator is declared and in line 17 the instance of the EventGenerator is created. Notice how the random variable representing the time between arrivals is provided to the EventGenerator constructor. The EventGenerator class uses classes that implement the EventGeneratorActionIfc interface. This interface defines a single method, called generate(), which is called to supply logic when the generated event occurs. An inner class called Arrivals implements the EventGeneratorActionIfc interface. Notice how a counter is used to count the number of events and a different counter is used to count the number of arrivals based on the random variable representing the number of occurrences governed by the discrete empirical distribution function.

public class EventGeneratorCPP extends SchedulingElement {

    protected EventGenerator myArrivalGenerator;
    protected Counter myEventCounter;
    protected Counter myArrivalCounter;
    protected RandomVariable myTBA;
    protected RandomVariable myNumArrivals;

    public EventGeneratorCPP(ModelElement parent) {
        this(parent, 1.0, null);
    }

    public EventGeneratorCPP(ModelElement parent, double tba, String name) {
        super(parent, name);
        double[] values = {1, 2, 3};
        double[] cdf = {0.2, 0.5, 1.0};
        myNumArrivals = new RandomVariable(this, new DEmpiricalRV(values, cdf));
        myTBA = new RandomVariable(this, new ExponentialRV(tba));
        myEventCounter = new Counter(this, "Counts Events");
        myArrivalCounter = new Counter(this, "Counts Arrivals");
        myArrivalGenerator = new EventGenerator(this, new Arrivals(), myTBA, myTBA);
    }

    protected class Arrivals implements EventGeneratorActionIfc {
        @Override
        public void generate(EventGenerator generator, JSLEvent event) {
            myEventCounter.increment();
            int n = (int)myNumArrivals.getValue();
            myArrivalCounter.increment(n);
        }
    }
}

The EventGenerator class allows for the periodic generation of events similar to that achieved by “Create” modules in other simulation languages. This class works in conjunction with the EventGeneratorActionIfc interface, which is used to listen and react to the events that are generated by this class. Users of the class can supply an instance of an EventGeneratorActionIfc to provide the actions that take place when the event occurs. Alternatively, if no EventGeneratorActionIfc is supplied, by default the generator(JSLEvent event) method of this class will be called when the event occurs. Thus, sub-classes can simply override this method to provide behavior for when the event occurs. If no instance of an EventGeneratorActionIfc instance is supplied and the generate() method is not overridden, then the events will still occur; however, no meaningful actions will take place. The key input parameters to the EventGenerator include:

time until the first event: This parameter is specified with an object that implements the RandomIfc. It should be used to represent a positive real value that represents the time after time 0.0 for the first event to occur. If this parameter is not supplied, then the first event occurs at time 0.0.
time between events: This parameter is specified with an object that implements the RandomIfc. It should be used to represent a positive real value that represents the time between events. If this parameter is not supplied, then the time between events is positive infinity.
time until last event: This parameter is specified with an object that implements the RandomIfc. It should be used to represent a positive real value that represents the time that the generator should stop generating. When the generator is created, this variable is used to set the ending time of the generator. Each time an event is to be scheduled the ending time is checked. If the time of the next event is past this time, then the generator is turned off and the event will not be scheduled. The default is positive infinity.
maximum number of events: A value of type long that supplies the maximum number of events to generate. Each time an event is to be scheduled, the maximum number of events is checked. If the maximum has been reached, then the generator is turned off. The default is Long.MAX_VALUE. This parameter cannot be Long.MAX_VALUE when the time until next always returns a value of 0.0.
listener: This parameter can be used to supply an instance of EventGeneratorListenerIfc interface to supply logic to occur when the event occurs.

The most common use case for an EventGenerator is very similar to the compound Poisson process example. The EventGenerator is setup to run with a time between events until the simulation completes; however, there are a number of other possibilities that are facilitated through various method associated with the EventGenerator class. The first possibility is to sub-class the EventGenerator to make a custom generator for objects of a specific class. To facilitate this the user need only implement the generate() method that is part of the EventGenerator class. For example, you could design classes to create customers, parts, trucks, demands, etc.

In addition to customization through sub-classes, there are a number of useful methods that are available for controlling the EventGenerator.

turnOffGenerator(): This method allows an EventGenerator to be turned off. The next scheduled generation event will not occur. This method will cancel a previously scheduled generation event if one exists. No future events will be scheduled after turning off the generator. Once the generator has been turned off, it cannot be restarted until the next replication.
turnOnGenerator(GetValueIfc t): If the generator was not started upon initialization at the beginning of a replication, then this method can be used to start the generator. The generator will be started \(t\) time units after the call. If this method is used when the generator is already started it does nothing. If this method is used after the generator is done it does nothing. If this method is used after the generator has been suspended it does nothing. In other words, if the generator is already on, this method does nothing.
suspend(): This method suspends the event generation pattern. The generator is still on, but the generation of events is suspended. The next scheduled generation event is canceled.
resume(): If the generator is suspended then this method causes the event generator to proceed with the event generation pattern by scheduling a new event according to the time between event distribution.
isSuspended(): Checks if the generator is suspended.
isGeneratorDone(): Checks if the generator has been turned off. The generator can be turned off via the turnOffGenerator() method or it may turn off when it has reached its time until last event or if the maximum number of events is reached. As previously noted, once a generator has been turned off, it cannot be turned on again within the same replication.

In considering these methods, a generator can turn itself off (as an action) within or caused by the code within its generate() method or in the supplied EventGeneratorListenerIfc interface. It might also suspend() itself in a similar manner. Of course, a class that has a reference to the generator may also turn it off or suspend it. To resume a suspended event generator, it is necessary to schedule an event whose action invokes the resume()method. Obviously, this can be within a sub-class of EventGenerator or within another class that has a reference to the event generator.

References

Ross, S. 1997. Introduction to Probability Models. 6th ed. Academic Press.

See (Ross 1997) for more information on the theory of compound Poisson processes.↩︎