3.7 Stochastic Activity Networks

A stochastic activity network (SAN) is a common modeling paradigm often used to represent project networks and other forms of network modeling. An activity network consists of a set of activities that have an ordered precedence indicating the dependence between the activities. For example, an activity C might not be able to start until both activities A and B are completed. Thus, (A, B) precede C in the network. A common question in such networks is how to determine the critical path or the longest path in the network. The following example will illustrate how to simulate a simple SAN to estimate the expected length of the critical path and estimate probabilities associated with time to complete the network.

---

Example 3.12 (Project Network) Consider a project consisting of nine jobs (A, B, \(\cdots\), I) with the precedence relationships and activity times. The table provides the minimum, mode, and maximum for each activity. We will assume that the activity times can be modeled using a triangular distribution with the appropriate parameters.

Job	Predecessors	Min	Mode	Max
A	-	2	5	8
B	A	6	9	12
C	A	6	7	8
D	B,C	1	4	7
E	A	7	8	9
F	D,E	5	14	17
G	C	3	12	21
H	F,G	3	6	9
I	H	5	8	11

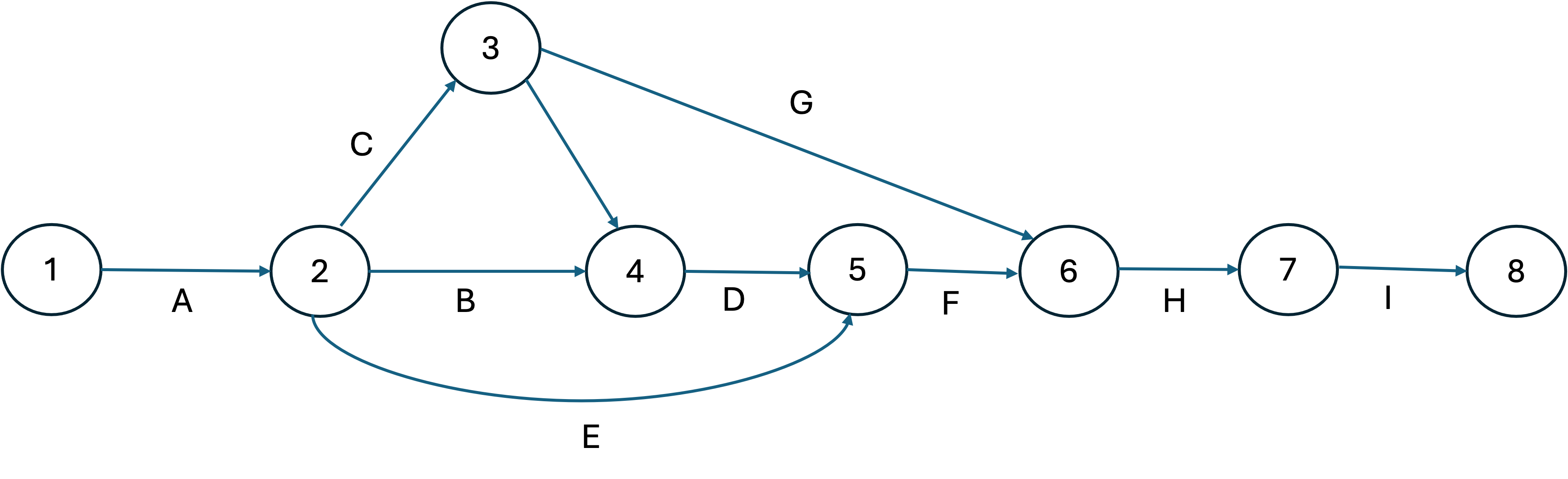
Figure 3.6: Project Network Diagram

Develop a simulation model that will estimate the expected time to completion for the project. In addition, estimate the probability that the project will be completed within 50 days. Finally, estimate the probability that the project will be completed between 42 and 48 days.

---

The key to modeling this situation is representing the data associated with the network. The longest path in the network will depend upon the random activity times. A simple approach to the determining the longest path in the network is to enumerate the paths. Then, we can randomly generate the time associated with each activity. From the random times, we can determine the length of each path. If we know the length of each path, then we can compute the path that is the longest.

In the following code, we represent the activities and the associated activity time (triangular) distributions using a map.

    val activityRVs = mapOf<String, TriangularRV>(
        "A" to TriangularRV(2.0, 5.0, 8.0),
        "B" to TriangularRV(6.0, 9.0, 12.0),
        "C" to TriangularRV(6.0, 7.0, 8.0),
        "D" to TriangularRV(1.0, 4.0, 7.0),
        "E" to TriangularRV(7.0, 8.0, 9.0),
        "F" to TriangularRV(5.0, 14.0, 17.0),
        "G" to TriangularRV(3.0, 12.0, 21.0),
        "H" to TriangularRV(3.0, 6.0, 9.0),
        "I" to TriangularRV(5.0, 8.0, 11.0),
    )

If you look closely at Figure 3.6, you can discern that there are four unique paths through the network. Since the paths are clear for this example, we can represent the paths with a list of lists.

    val paths = mutableListOf<List<String>>(
        listOf("A", "B", "D", "F", "H", "I"),
        listOf("A", "E", "F", "H", "I"),
        listOf("A", "C", "D", "F", "H", "I"),
        listOf("A", "B", "C", "G", "H", "I"),
    )

This data structure will allow each path to be enumerated to determine the length of the network once the random activity times have been realized. In general, for large networks, this enumeration approach will not be the best approach and specialized algorithms will be required to find the longest path.

Now that we have the data structures for holding the activity times and the paths, we can write functions that can take advantage of the data structures. The first function that we will write will randomly generate the activity times for the network. That is, in essence, randomly generate the time for each arc (activity) of the network. This can be accomplished by iterating through the activity map.

fun generateActivityTimes(activities: Map<String, TriangularRV>) : Map<String, Double> {
    val map = mutableMapOf<String, Double>()
    for ((name, rv) in activities){
        map[name] = rv.value
    }
    return map
}

In this code, the activities map is iterated for each activity and the associated random variable is called to generate the associated activity time. The realized activity time is stored in an outgoing map that holds the activity name and its activity time. This map holds a realized network. From a realized network, we can enumerate the paths to determine the longest path and thus the completion time. This idea is implemented in the following function.

fun timeToCompletion(activityTimes: Map<String, Double>, paths: List<List<String>>): Double {
    val times = mutableListOf<Double>()
    for (path in paths) {
        var pathTime = 0.0
        for (activity in path) {
            pathTime = pathTime + activityTimes[activity]!!
        }
        times.add(pathTime)
    }
    return times.max()
}

In this code, each path in the provided list of paths is enumerated. The time to complete the path is the sum of the individual activity times on the path. Once we have all the total path lengths computed, we can easily use the max() function of the Kotlin collection library to determine the maximum time, which is returned as the time to complete the realization of the sample network. Now, we are ready to simulate many instances of the network to collect statistics associated with the expected performance and probability of completion. The following code puts these ideas into action.

    val timeToCompleteStat = Statistic("Time to Completion")
    val probLT50Days = Statistic("P(T<=50)")
    val probWith42and48Days = Statistic("P(42<=T<=48)")
    val interval = Interval(42, 48)
    val sampleSize = 1000
    for (i in 1..sampleSize) {
        val a = generateActivityTimes(activityRVs)
        val t = timeToCompletion(a, paths)
        timeToCompleteStat.collect(t)
        probLT50Days.collect(t <= 50)
        probWith42and48Days.collect(interval.contains(t))
    }
    val sr = StatisticReporter(mutableListOf(timeToCompleteStat, probLT50Days, probWith42and48Days))
    println(sr.halfWidthSummaryReport())

In this code, we randomly generate 1000 networks and thus 1000 completion times. As in previous examples, instances of the Statistic class are used to collect and report statistics for the simulation.

Statistical Summary Report

Name	Count	Average	Half-Width
Time to Completion	1000.0	47.80137141578008	0.24824203870040715
P(T<=50)	1000.0	0.7010000000000005	0.02842407807532723
P(42<=T<=48)	1000.0	0.4729999999999999	0.03099757091483164

The results indicate that on average it takes about 47.8 days to complete the network. In the following section, we explore generalizing the execution of Monte Carlo experiments.