6.2 The Process View
Before introducing the many of the technical details of processing modeling within the KSL, we will start with a simple example. The example will again be the drive through pharmacy model but in this section it will be implemented using the process modeling constructs available within the KSL.
Recall that we have a small pharmacy that has a single line for waiting customers and only one pharmacist. Assume that customers arrive at a drive through pharmacy window according to a Poisson distribution with a mean of 10 per hour. The time that it takes the pharmacist to serve the customer is random and data has indicated that the time is well modeled with an exponential distribution with a mean of 3 minutes. Customers who arrive to the pharmacy are served in the order of arrival and enough space is available within the parking area of the adjacent grocery store to accommodate any waiting customers.
Figure 6.2: Drive Through Pharmacy
The drive through pharmacy system can be conceptualized as a single server waiting line system, where the server is the pharmacist. An idealized representation of this system is shown in Figure 6.2. In Section 4.4.4 of Chapter 4, we presented an activity diagram for the pharmacy.
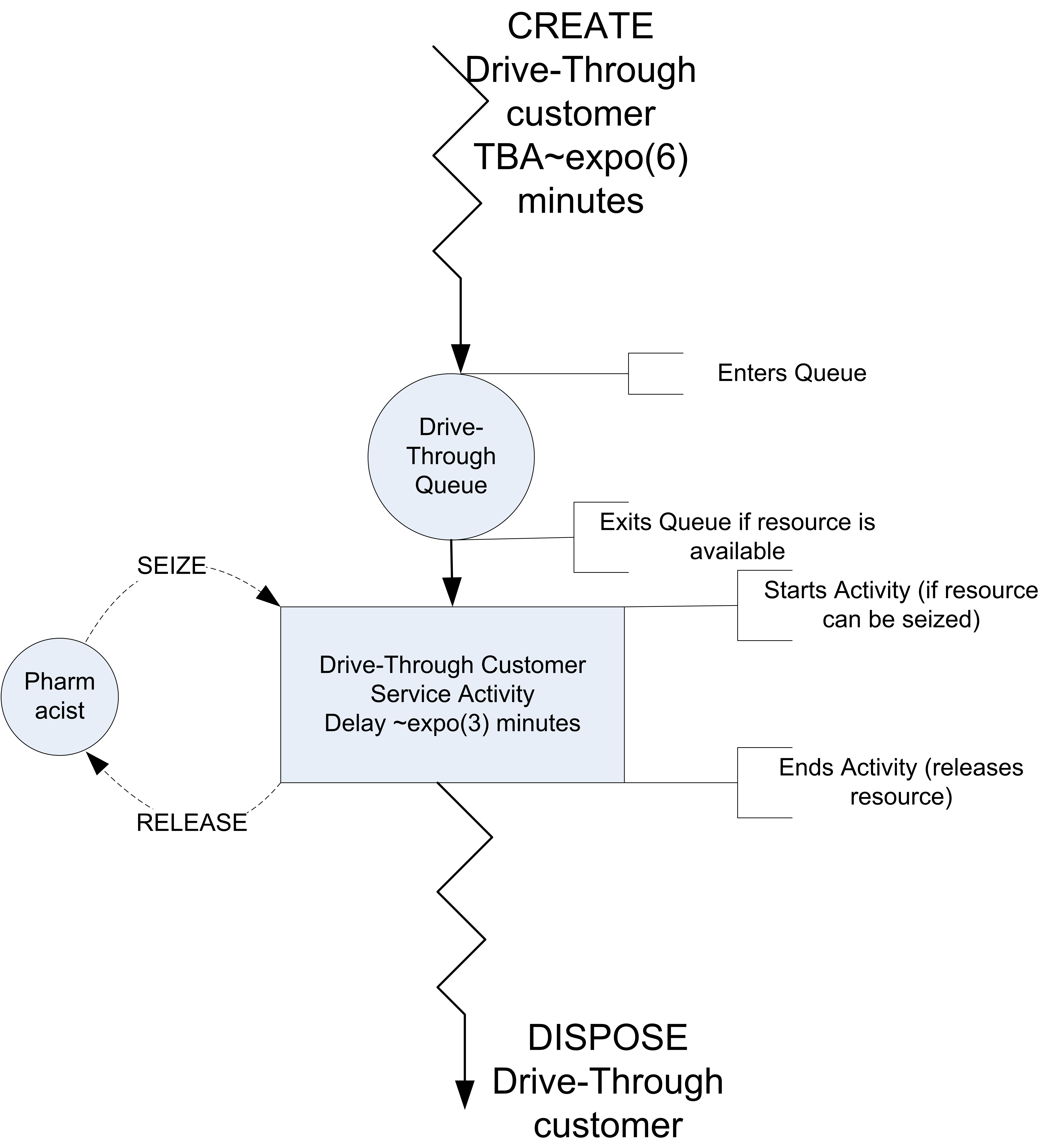
Figure 6.3: Activity Diagram of Drive through Pharmacy
The activity diagram is a basic description of the process experienced by the customer. In Chapter 4, we used the activity diagram to identify the arrival and end of service events. In this chapter, we will almost directly translate the activity diagram to KSL code.
Here is the portion of the KSL code to model the process for the customers of the drive through pharmacy:
private inner class Customer : Entity() {
val pharmacyProcess: KSLProcess = process() {
wip.increment()
timeStamp = time
val a = seize(worker)
delay(serviceTime)
release(a)
timeInSystem.value = time - timeStamp
wip.decrement()
numCustomers.increment()
}
}The code defines a class called Customer which is a subclass of Entity. The Entity class is a base class that encapsulates the ability to experience processes. Now, notice the definition and initialization of the variable pharmacyProcess within the Customer class. This is a very special function builder that allows for the definition of a coroutine that defines the process for the entity. Coroutines are software constructs that permit the suspension and resumption of programming statements. Kotlin supports the use of coroutines for asynchronous programming. In this situation, the KSL leverages Kotlin’s coroutine library to implement the process view.
Example 6.1 (Process View Model for Drive Through Pharmacy System) This example illustrates how to represent the previously presented drive through pharmacy model of Example 4.4 in Section 4.4.4 using KSL process view constructs.
class DriveThroughPharmacy(
parent: ModelElement,
numPharmacists: Int = 1,
ad: RandomIfc = ExponentialRV(1.0, 1),
sd: RandomIfc = ExponentialRV(0.5, 2),
name: String? = null
) : ProcessModel(parent, name) {
init {
require(numPharmacists > 0) { "The number of pharmacists must be >= 1" }
}
private val pharmacists: ResourceWithQ = ResourceWithQ(this, "Pharmacists", numPharmacists)
private var serviceTime: RandomVariable = RandomVariable(this, sd)
val serviceRV: RandomSourceCIfc
get() = serviceTime
private var timeBetweenArrivals: RandomVariable = RandomVariable(parent, ad)
val arrivalRV: RandomSourceCIfc
get() = timeBetweenArrivals
private val wip: TWResponse = TWResponse(this, "${this.name}:NumInSystem")
val numInSystem: TWResponseCIfc
get() = wip
private val timeInSystem: Response = Response(this, "${this.name}:TimeInSystem")
val systemTime: ResponseCIfc
get() = timeInSystem
private val numCustomers: Counter = Counter(this, "${this.name}:NumServed")
val numCustomersServed: CounterCIfc
get() = numCustomers
private val mySTGT4: IndicatorResponse = IndicatorResponse({ x -> x >= 4.0 }, timeInSystem, "SysTime > 4.0 minutes")
val probSystemTimeGT4Minutes: ResponseCIfc
get() = mySTGT4
override fun initialize() {
schedule(this::arrival, timeBetweenArrivals)
}
private fun arrival(event: KSLEvent<Nothing>) {
val c = Customer()
activate(c.pharmacyProcess)
schedule(this::arrival, timeBetweenArrivals)
}
private inner class Customer : Entity() {
val pharmacyProcess: KSLProcess = process() {
wip.increment()
timeStamp = time
val a = seize(pharmacists)
delay(serviceTime)
release(a)
timeInSystem.value = time - timeStamp
wip.decrement()
numCustomers.increment()
}
}
}Most of this code should look very familiar. It includes the definition of the random variables to model the time between arrivals and service time. It also defines the responses to collect statistics on the performance of the system. In addition, it uses the functional notation for referencing functional interfaces to schedule the arrival events. Within the arrival event, the customer is created and it is told to activate() its process.
The process called pharmacyProcess has a nice linear flow and avoids the event call back approach of the event-view. The first line wip.increment() simply increments the number of customers in the system. The next line involving timeStamp assigns the arrival time of the customer. Then, the customer attempts to seize the pharmacist. If the pharmacist is available, it is allocated to the customer. The variable “a” holds the allocation information. If a pharmacist is not available, the customer is held in a queue related to the invocation of the seize() function. The seize() function is a suspending function. This is the magic of coroutines. The execution of the coroutine literally stops within the seize() function if the pharmacist is not available. When the pharmacist becomes available, the customer (and suspended code) resumes moving through the process. The delay() function is another suspending function. The delay function essentially schedules an event to represent the service time and when the event occurs the coroutine is resumed. The release() deallocates the resource from the customer. The final three lines simply collect statistical quantities.
It is critical to understand that 1) there are many entities created via the arrival method, 2) they all experience the same process description, 3) each entity has its own instance of the process, and 4) they may all be at different points of their process instances at different times. Since many customers are active at the same time (in a pseudo-parallelism) they compete for the pharmacist. This causes queueing. This process view depends on shared state. In this example, the primary shared state is via the resource. This is a new construct and was defined with the following line.
A ResourceWithQ is a construct that can be used in ProcessModel instances. These resources track the number of entities that are allocated and can hold them in a common queue while they wait. The ability to describe processes in this manner is what makes the process view very popular and often serves as the basis for commercial software. The KSL provides this view in open-source code.
If we run the code, we get the following results.
Half-Width Statistical Summary Report - Confidence Level (95.000)%
Name Count Average Half-Width
------------------------------------------------------------------------------------
NumBusy 30 0.5035 0.0060
# in System 30 1.0060 0.0271
System Time 30 6.0001 0.1441
PharmacyQ:NumInQ 30 0.5025 0.0222
PharmacyQ:TimeInQ 30 2.9961 0.1235
SysTime > 4.0 minutes 30 0.5136 0.0071
Num Served 30 2513.2667 17.6883
----------------------------------------------------------------------------------------- If you look back at the previous results, you will see that these results are exactly the same! Thus, we can model the pharmacy with either the event view or the process view with confidence.
Before discussing additional functionality enabled within the KSLProcessBuilder, we present some functionality that facilitates the creation and activation of entities. Notice that within the pharmacy model that after an customer is created to start its process we must schedule its activation.
private fun arrival(event: KSLEvent<Nothing>) {
val c = Customer()
activate(c.pharmacyProcess)
schedule(this::arrival, timeBetweenArrivals)
}This is so common the KSL provides a class called EntityGenerator that automates this process. The EntityGenerator class subclasses from EventGenerator and allows for a creation pattern to be specified. Figure 6.4 illustrates this relationship.
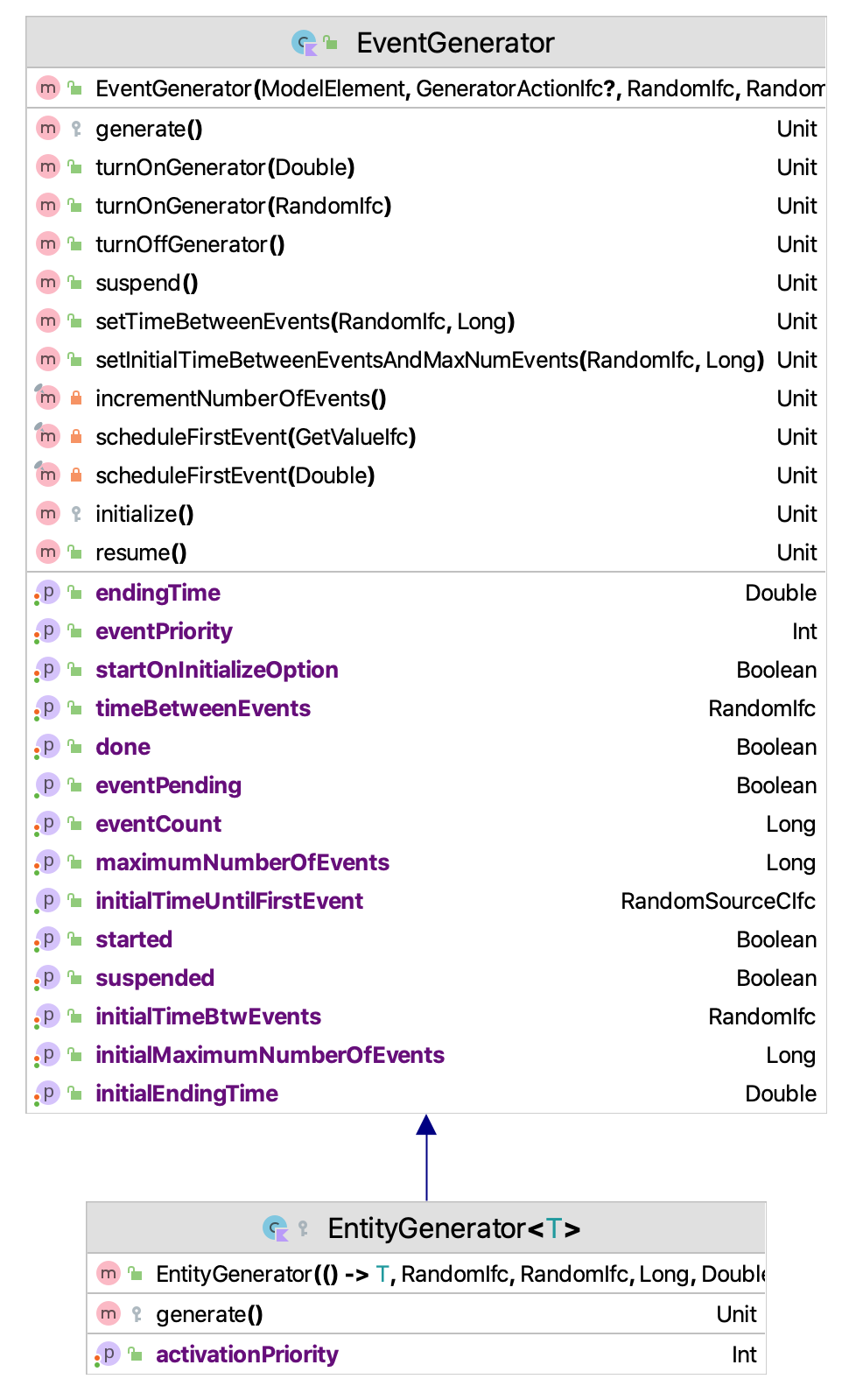
Figure 6.4: Overview of the ProcessModel Class
The EntityGenerator class is defined as an inner class of ProcessModel. Reviewing its code is useful.
protected inner class EntityGenerator<T : Entity>(
private val entityCreator: () -> T,
timeUntilTheFirstEntity: RandomIfc = ConstantRV.ZERO,
timeBtwEvents: RandomIfc = ConstantRV.POSITIVE_INFINITY,
maxNumberOfEvents: Long = Long.MAX_VALUE,
timeOfTheLastEvent: Double = Double.POSITIVE_INFINITY,
var activationPriority: Int = KSLEvent.DEFAULT_PRIORITY + 1,
name: String? = null
) : EventGenerator(
this@ProcessModel, null, timeUntilTheFirstEntity,
timeBtwEvents, maxNumberOfEvents, timeOfTheLastEvent, name
) {
override fun generate() {
val entity = entityCreator()
require(entity.defaultProcess != null) {"There was no initial process specified for the entity"}
activate(entity.defaultProcess!!, priority = activationPriority)
}
}As shown in the code, the key additional functionality is that the EntityGenerator takes in a function that knows how to create a subclass of type Entity. The simplest way to provide such a function is to provide a reference to the constructor function of the subclass. This is illustrated in the following simplified re-do of the pharmacy model.
Example 6.2 (Demonstrating an Entity Generator) This example illustrates how to construct an instance of the EntityGenerator class and use it to create entity instances according to a time between event pattern.
class EntityGeneratorExample(
parent: ModelElement,
name: String? = null
) : ProcessModel(parent, name) {
private val worker: ResourceWithQ = ResourceWithQ(this, "${this.name}:Worker")
private val tba = ExponentialRV(6.0, 1)
private val st = RandomVariable(this, ExponentialRV(3.0, 2))
private val wip = TWResponse(this, "${this.name}:WIP")
private val tip = Response(this, "${this.name}:TimeInSystem")
private val generator = EntityGenerator(::Customer, tba, tba)
private val counter = Counter(this, "${this.name}:NumServed")
private inner class Customer : Entity() {
val pharmacyProcess: KSLProcess = process(isDefaultProcess = true) {
wip.increment()
timeStamp = time
val a = seize(worker)
delay(st)
release(a)
tip.value = time - timeStamp
wip.decrement()
counter.increment()
}
}
}Notice the following line which takes in a reference to the Customer class constructor using the functional syntax ::Customer. In addition, notice the specification of the isDefaultProcess argument for the process() function. Setting the isDefaultProcess argument to true indicates that the defined process routine will be the default process to be activated when the EntityGenerator causes the generation event to occur.
There is no arrival method necessary because that logic is within the entity generator’s generate() method:
override fun generate() {
val entity = entityCreator()
require(entity.defaultProcess != null) {"There was no initial process specified for the entity"}
activate(entity.defaultProcess!!, priority = activationPriority)
}The entity is created using the passed in constructor function and the entity’s default process is started. By default, the process() function of the KSLProcessBuilder class automatically adds each newly defined named process to the entity’s map of named processes. If the name argument is not supplied, then the defined process is not added to the process map. The map of named processes for an entity can be accessed via the processes property of the Entity class.
To specify the default process, provide the isDefaultProcess argument of the process() function to be true. Thus, by using an instance of an EntityGenerator associated with a particular subclass of Entity, we can automatically create the instances of the subclass and activate their processes. Of course, the creation of the subclass (e.g. Customer) might be much more complex; however, the EntityGenerator takes in a function that creates the instance of the subclass. Thus, it can be any function, not just the constructor function. Therefore, instances can be configured in complex ways before they are activated by supplying an appropriate function.
IMPORTANT!
Note that an EntityGenerator relies on the entity having a default process defined via the process() method. An entity generator will create the entity and start the process that is defined as the default process. Rather than use the process() function, you can directly specify the default process via the defaultProcess property of the Entity class. If you try to use an EntityGenerator without a defined default process, then an illegal state exception will occur.
In the next section, we will take a closer look at how the KSL makes the process view possible. This will help you to better use the process modeling capabilities found in the KSL.