4.6 More Drive Through Fun

Many fast food franchises have configured their restaurants such that customers using the drive through option first place an order at an ordering station and then pickup and pay at following station. This situation is called a tandem queueing system as illustrated in Figure 4.13. This section presents KSL constructs that facilitate the modeling of simple queueing situations, like that faced by fast food drive through lines.

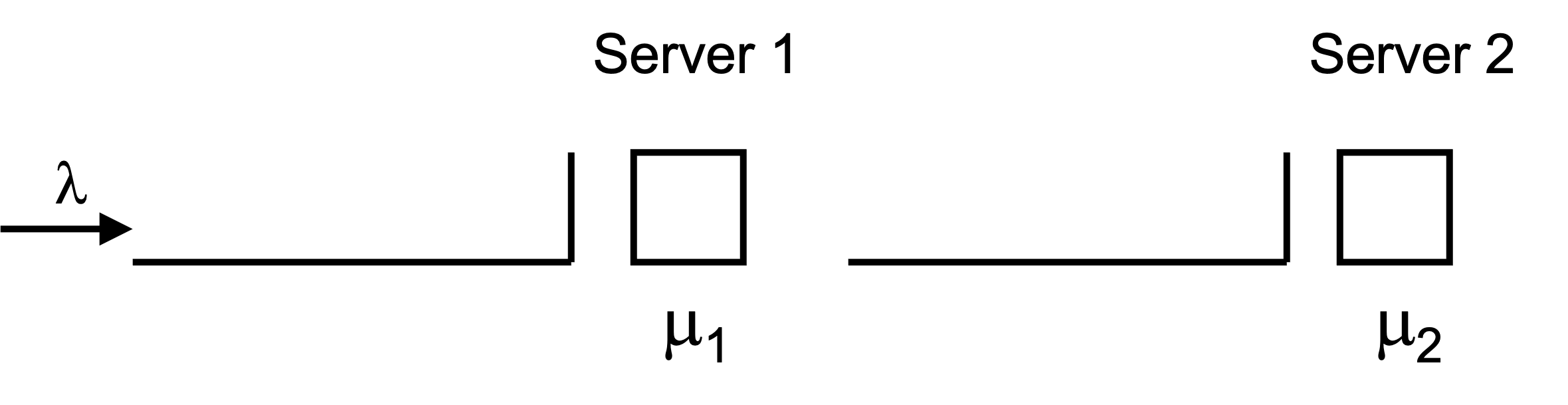
Figure 4.13: Tandem Queue

A tandem queue is a sequence of queues that must be visited (in order) to receive service from resources. The following example presents an illustrative situation.

---

Example 4.6 (Tandem Queueing System) Suppose a service facility consists of two stations in series (tandem), each with its own FIFO queue. Each station consists of a queue and a single server. A customer completing service at station 1 proceeds to station 2, while a customer completing service at station 2 leaves the facility. Assume that the inter-arrival times of customers to station 1 are IID exponential random variables with a mean of 6 minutes. Service times of customers at station 1 are exponential random variables with a mean of 4 minute, and at station 2 are exponential random variables with mean 3 minute. Develop an model for this system. Run the simulation for 30 replications of 20000 minutes, with a warm up period of 5000 minutes. Estimate for each station the expected average delay in queue for the customer, the expected time-average number of customers in queue, and the expected utilization. In addition, estimate the average number of customers in the system and the average time spent in the system.

---

The first thing to note about this situation is that the system consists of two very similar components: station 1 and station 2. The second thing to note is that the same types of events occur for each of the two components. That is, there are arrival and departure events for each station. The state change logic for the arrival and departure events is exactly the same as we saw for the pharmacy situation:

Arrival Actions for Event \(E_a\)

N(t) = N(t) + 1
if (B(t) < c)
  B(t) = B(t) + 1
  schedule E_s at time t + ST_i
else
  Q(t) = Q(t) + 1
endif
schedule E_a at time t + TBA_i

We increase the number in the system \(N(t)\) by 1 and check if the number of busy servers \(B(t)\) is less than the capacity \(c\). If so, we start the customer into service; otherwise, we place the customer in the queue.

End of Service Actions for Event \(E_s\)

B(t) = B(t) - 1
if (Q(t) > 0)
  Q(t) = Q(t) - 1
  B(t) = B(t) + 1
  schedule E_s at time t + ST_i
endif
N(t) = N(t) - 1

The end of service actions are as previously seen. There is one less server busy and if the queue has customers, it is processed and the customer’s service starts. Since the same logic will need to be implemented for each station, it makes sense from an object-oriented perspective, to conceptualize a class that encapsulates the data and behavior to represent this situation.

Figure 4.13 should give an idea of what the class should represent. In the figure, there are two stations with each station containing a queue and a server (or resource). Thus, we should build a class that models a single queue that holds objects that must wait for a server to be available. We are going to call this thing a SingleQStation. Notice that the input to the first station is a customer from some arrival process and that the input to the second station is a customer departing the first station. Thus, the main difference between how these components act is where they receive customers from and where they send completed customers. Notice that a station needs to know where to send its completed customers. What else does a station need to know in order to process the customers? The station will need to know how many servers are available at the station and will need to know how to determine the processing time for the customers. For this modeling, we need to expand on the concept of a resource.

4.6.1 Modeling a Simple Resource

As we saw in the drive through pharmacy example, when the customer arrives they need the pharmacist in order to proceed. As noted in the activity diagram depicted in Figure 4.9, we denoted the pharmacist as a resource (circle) in the diagram. A resource is something that is needed by the objects (or entities) that experience the system’s activities. In the pharmacy model, the resource (pharmacist) was required to start the service activity, denoted with a arrow with the word “seize” in the activity diagram, pointing from the resource to the start of the activity. After the activity is completed, there is a corresponding arrow labeled “release” pointing from the end of the activity back to the resource. This arrow denotes the returning of the used resource units back to the pool of available units.

As we can see from Figure 4.13 our concept of a SingleQStation also contains a resource. Since the same concept is within both stations, it seems useful to represent the concept of a resource with a class. For the purposes of this situation, we are going to denote the concept of a simple resource with the aptly named SResource class (for simple resource). Let’s take a look at how the KSL represents a simple resource.

Figure 4.14: A Simple Resource Class

A resource has a capacity that represents the maximum number of units that it can have available at any time. When a resource is seized some amount of units become busy (or allocated). When the units are no longer needed, they are released. If we let \(A(t)\) be the number of available units, \(B(t)\) be the number of busy units and \(c\) be the capacity of the resource, we have that \(c = A(t) + B(t)\) or \(A(t) = c - B(t)\). A resource is considered busy if \(B(t) > 0\). That is, a resource is busy if some units are allocated. A resource is considered idle if no units are busy. That is, \(B(t) = 0\), which implies that \(A(t) = c\).

If the number of available units of a resource are unable to meet the number of units required by a “customer”, then we need to decide what to do. To simplify this modeling, we are going to assume two things 1) customers only request 1 unit at a time, and 2) if the request cannot be immediately supplied the customer will wait in an associated queue. These latter two assumptions are essentially what we have assumed in the modeling of the pharmacy situation and in the situation described in Example 4.6. Modeling often requires the use of simplifying assumptions.

The SResource class of Figure 4.14 has functions seize() and release() which take (seize) and return (release) units of the resource. It also has properties (busy and idle) that indicate if the resource is busy or idle, respectively. In addition, the property numBusyUnits represents \(B(t)\) and the property numAvailableUnits represents \(A(t)\). For convenience, the hasAvailableUnits property indicates if the resource has units that can be seized. Finally, the number of times the resource is seized and released are tabulated. The main performance measures are time weighted response variables for tabulating the time-average number of busy units and the time-average instantaneous utilization of the resource. Instantaneous utilization, \(U(t)\) is governed by tracking \(U(t) = B(t)/c\). Now that we have a way to represent a resource, let’s put the resource together with a queue to get a station for processing in the SingleQStation class.

4.6.2 Modeling a Resource with a Waiting Line

The SingleQStation class will use an instance of the SResource class to represent its resource. In addition, the SingleQStation class will use an instance of the Queue class presented in the previous section to represent the waiting line for the customers that need to wait for their requested units of the resource. The customers that use the single queue station will be represented by instances of the QObject class. We are now ready to put most of these pieces together to construct the SingleQStation class. Once we have an understanding of the SingleQStation class, we will be ready to model Example 4.6.

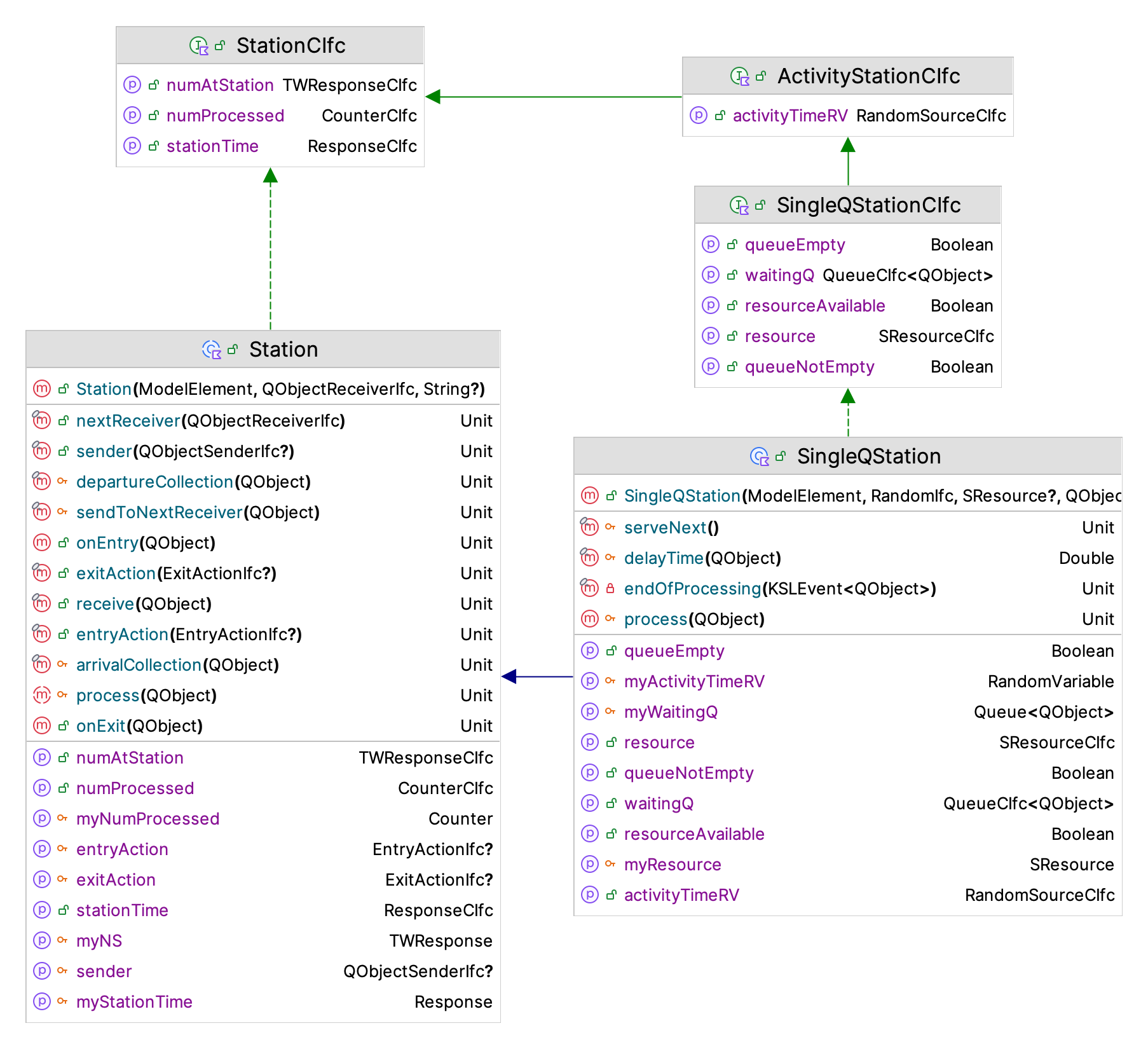
Figure 4.15: The SingleQStation Class

Let’s start with an overview of the functionality of the SingleQStation class and then review the code implementation. Figure 4.15 presents the constructor, functions, and properties of the SingleQStation class. The main item to note about the constructor is that it can take in an instance of the SResource class. The second thing to note is that instances can process instances of the QObject class via the process() function. The process() function represents the actions that should occur when something arrives to the station. The endOfProcessing() function represents what should happen when the processing is completed. That is, the process() function is the “arrival event” and the endOfProcessing() function is the “departure event”. Let’s look at the code.

The logic of the process() function should look very familiar. Just as was done in previous examples, the arriving customer immediately enters the queue. Then, if the resource is available, the next customer is placed into service.

    /**
     *  Receives the qObject instance for processing. Handle the queuing
     *  if the resource is not available and begins service for the next customer.
     */
    override fun process(arrivingQObject: QObject) {
        // enqueue the newly arriving qObject
        myWaitingQ.enqueue(arrivingQObject)
        if (isResourceAvailable) {
            serveNext()
        }
    }

The serveNext() function removes the next customer from the queue, seizes the resource, and schedules the end of processing event for the customer. Notice that the customer starting service is attached to the event. Note that the purpose of the delayTime() function is to determine the processing time for the customer when using the resource. There are two default options available. The delay can be supplied from the QObject instance via the valueObject property. If attached to the QObject instance the valueObject property returns something that returns a Double value. This value can be used for anything you want it to represent. In this case, it can be used to supply a delay time. The second option is to use the processing time that was specified for the station if the value object is not attached to the QObject instance.

    /**
     * Called to determine which waiting QObject will be served next Determines
     * the next customer, seizes the resource, and schedules the end of the
     * service.
     */
    protected fun serveNext() {
        //remove the next customer
        val nextCustomer = myWaitingQ.removeNext()!!
        myResource.seize()
        // schedule end of service, if the customer can supply a value,
        // use it otherwise use the processing time RV
        schedule(this::endOfProcessing, delayTime(nextCustomer), nextCustomer)
    }

    /**
     *  Could be overridden to supply different approach for determining the service delay
     */
    protected fun delayTime(qObject: QObject) : Double {
        return qObject.valueObject?.value ?: myActivityTimeRV.value
    }

As mentioned, the endOfProcessing() function represents the logic that should occur after the customer completes its use of the resource for the processing time. In the following code, first the customer completing service is grabbed from the event’s message. After releasing the resource, the queue is checked and if it is not empty the next customer is started into service. Then, the leaving customer exits the station and is sent to the next location. The function sendToNextReceiver() will be discussed further within the context of the example.

    /**
     *  The end of processing event actions. Collect departing statistics and send the qObject
     *  to its next receiver. If the queue is not empty, continue processing the next qObject.
     */
    private fun endOfProcessing(event: KSLEvent<QObject>) {
        val leaving: QObject = event.message!!
        myResource.release()
        if (isQueueNotEmpty) { // queue is not empty
            serveNext()
        }
        sendToNextReceiver(leaving)
    }

There is a lot more happening withing the SingleQStation class than presented here. As you can see from Figure 4.15, the SingleQStation class inherits from the Station class, which is an abstract base class. The Station class ensures that statistics that are common to all station types are collected. In addition, the Station class provides for the attachment of functions that may be executed when something arrives to the station and also when something departs. Such entry and exit actions provide users the ability to add behavior to a station without having to use inheritance via the use of Kotlin lambda functions. Entry and exit actions are represented by single abstract method (SAM) via the EntryActionIfc and ExitActionIfc interfaces. Lambda expressions can be attached to a station to effect useful logic.

We now have a new KSL class that can be used to model many different situations (like the drive through pharmacy) that involve the use of resources and waiting lines. Let’s continue this by implementing the model for Example 4.6. This will motivate how to send and receive QObject instances.

4.6.3 Modeling the Tandem Queue of Example 4.6

The main concepts needed to put the pieces together to represent the tandem queue described in Example 4.6 are now modeled. The main remaining concept needed is how to send and receive customers within such systems. Since this is a very common requirement, the KSL provides basic functionality to help with this modeling task. Two new KSL constructs will be introduced and then used within the implementation of the tandem queue model. The first is an interface that promises to allow the receiving of QObject instances: the QObjectReceiverIfc interface.

fun interface QObjectReceiverIfc {
    fun receive(qObject: ModelElement.QObject)
}

Note that the QObjectReceiverIfc interface is SAM functional interface. Classes that implement the QObjectReceiverIfc interface promise to have a receive() function. The idea is to have a defined protocol for system components that will do something with the received QObject instance. As you may now realize, the SingleQStation class implements the QObjectReceiverIfc interface via its inheritance from the Station class. As shown in the following code, the SingleQStation class extends the Station class, which implements the QObjectReceiverIfc interface.

open class SingleQStation(
    parent: ModelElement,
    activityTime: RandomIfc,
    resource: SResource? = null,
    nextReceiver: QObjectReceiverIfc = NotImplementedReceiver,
    name: String? = null
) : Station(parent, nextReceiver, name = name), SingleQStationCIfc {
...
}

Figure 4.16 presents the major classes and interfaces of the ksl.modeling.station package. Central to the functionality is the Station class and the QObjectReceiverIfc interface.

Figure 4.16: Major Classes and Interfaces of the Station Package

The QObjectReceiverIfc interface defines a protocol for receiving QObject instances and the Station class provides default functionality for receiving an arriving QObject instance and for sending a completed QObject instance to its next location. Reviewing the Station class’s code is useful to understanding how this works. The Station class is an abstract class that provides the sendToNextReceiver() function.

abstract class Station(
    parent: ModelElement,
    private var nextReceiver: QObjectReceiverIfc = NotImplementedReceiver,
    name: String? = null
) : ModelElement(parent, name), QObjectReceiverIfc, StationCIfc {

    /**
     *  Sets the receiver of qObject instances from this station
     */
    fun nextReceiver(receiver: QObjectReceiverIfc) {
        nextReceiver = receiver
    }
.
.
    protected fun sendToNextReceiver(completedQObject: QObject) {
        departureCollection(completedQObject)
        exitAction?.onExit(completedQObject)
        onExit(completedQObject)
        if (sender != null) {
            sender!!.send(completedQObject)
        } else {
            if (completedQObject.sender != null) {
                completedQObject.sender!!.send(completedQObject)
            } else {
                nextReceiver.receive(completedQObject)
            }
        }
    }
    
    /**
     *  Can be used to supply a sender that will be used instead of
     *  the default behavior. The default behavior uses a sender attached
     *  to the QObject instance and if not attached will send the QObject
     *  to the next receiver.
     */
    fun sender(sender: QObjectSenderIfc?) {
        this.sender = sender
    }

There are three mechanisms for determining where to send the departing QObject instance. The first mechanism allows the user to attach a QObjectSenderIfc instance via the sender() function. As you can see from the code, if this mechanism is supplied, then it is used to send the completed QObject instance somewhere (i.e. to some receiver). If this first mechanism is not supplied, then the station looks to see if the completed QObject instance has a specified sender. If it does, then the QObject instance’s sender is used for sending. Every QObject has an (optional) property called sender that (if set) should return an instance of a QObjectSenderIfc interface.

/**
 *  A functional interface that promises to send. Within the
 *  context of qObjects a sender should cause a qObject
 *  to be (eventually) received by a receiver.
 */
fun interface QObjectSenderIfc {
    fun send(qObject: ModelElement.QObject)
}

The idea is that the sender will know how to send its related QObject instance to a suitable receiver. Thus, complex routing logic could be attached to the QObject instance. The sendToNextReceiver() function checks to see if the the QObject instance has a sender to assist with its routing. If it does, the sender is used to get the next location and then sends the QObject instance to the location by telling the location to receive the object. If the sender is not present, then the nextReceiver property is used to send the QObject instance to the specified receiver. The receiver’s behavior determines what happens to the QObject instance next.

The final approach supplies the destination (receiver) as part of the creation of the station instance. Notice that the Station class takes in a parameter called nextReceiver which represents an object that implements the QObjectReceiverIfc interface. This parameter can be used to specify where the departing QObject instance should be sent. That is, the next object that should receive the departing object. The default value for this parameter is the NotImplementedReceiver object. This object will throw a not implemented yet exception if you do not replace it with something that models the situation. You need to replace the default NotImplementedReceiver object only if one of the other two mechanisms are not being used by the station.

NOTE! As you will soon see in the following example, creating a station without specifying a receiver can be very convenient. This is why the NotImplementedReceiver object is the default. However, if you forget to set the receiver to something useful or do not use one of the other mechanisms, you will get the not implemented yet error.

The approach of specifying the receivers to visit allows for the modeling of very complex systems by simply “hooking” up the object instances in the correct order. We can now illustrate this with the implementation of the example.

The following code presents the class constructor for the TandemQueue class. The class takes in the random variables need for the arrival and two service processes. Then, because of the requirement to report the total system time and the total number of customers in the system, we have standard definitions for time-weighted response variables and a counter. This is very similar to how we defined the pharmacy system.

class TandemQueue(
    parent: ModelElement,
    ad: RandomIfc = ExponentialRV(6.0, 1),
    sd1: RandomIfc = ExponentialRV(4.0, 2),
    sd2: RandomIfc = ExponentialRV(3.0, 3),
    name: String? = null
): ModelElement(parent, name) {

    private val myNS: TWResponse = TWResponse(this, "${this.name}:NS")
    val numInSystem: TWResponseCIfc
        get() = myNS

    private val mySysTime: Response = Response(this, "${this.name}:TotalSystemTime")
    val totalSystemTime: ResponseCIfc
        get() = mySysTime

    private val myNumProcessed: Counter = Counter(this, "${this.name}:TotalProcessed")
    val totalProcessed: CounterCIfc
        get() = myNumProcessed
...

Now, the real magic of the station package can be used. The following code represents the rest of the implementation of the tandem queue system. The code uses an EventGenerator instance to model the arrival process to the first station. Then, two instances of the SingleQStation class are created to represent the first and second station in the system. Notice the implementation of the init{} block. The nextReceiver property for station 1 is set to be the second station and the nextReceiver property for station 2 is set to an instance of the ExitSystem inner class. This approach relies on replacing the default NotImplementedReceiver receiver. Notice that if you did not rely on this default, you would need to create the stations (receivers) in the reverse order so that you could supply the correct receiver within the station’s constructor. The init{} block would not be necessary with that approach.

    private val myArrivalGenerator: EventGenerator = EventGenerator(this,
        this::arrivalEvent, ad, ad)

    private val myStation1: SingleQStation = SingleQStation(this, sd1, name= "${this.name}:Station1")
    val station1: SingleQStationCIfc
        get() = myStation1

    private val myStation2: SingleQStation = SingleQStation(this, sd2, name= "${this.name}:Station2")
    val station2: SingleQStationCIfc
        get() = myStation2

    init {
       myStation1.nextReceiver(myStation2)
       myStation2.nextReceiver(ExitSystem())
    }

    private fun arrivalEvent(generator: EventGenerator){
        val customer = QObject()
        myNS.increment()
        myStation1.receive(customer)
    }

    private inner class ExitSystem : QObjectReceiverIfc {
        override fun receive(qObject: QObject) {
            mySysTime.value = time - qObject.createTime
            myNumProcessed.increment()
            myNS.decrement()
        }
    }
}

The arrival process shown in the arrivalEvent() function creates the arriving customer, increments the number in the system, and tells station 1 to receive the customer. This will set off a series of events which will occur within the SingleQStation instances that eventually result in the customer being received by the ExitSystem instance. The ExitSystem instance is used to collect statistics on the departing customer. The modeling involves hooking up the system components so that they work together to process the customers. This creation and use of objects in this manner is a hallmark of object-oriented programming. The following code can be used to simulate the system.

fun main(){
    val sim = Model("TandemQ Model")
    sim.numberOfReplications = 30
    sim.lengthOfReplication = 20000.0
    sim.lengthOfReplicationWarmUp = 5000.0
    val tq = TandemQueue(sim, name = "TandemQ")
    sim.simulate()
    sim.print()
}

The results from running the following code are not very interesting except for noticing the number of statistics that are are automatically captured within the output. Notice for example that the resources automatically report the average number of busy units and the utilization of the resource. In addition, stations automatically report the total time spent at a station, the number of objects at the station, and the number completed by the station.

Statistical Summary Report

Name	Count	Average	Half-Width
TandemQ:NS	30	3.04	0.093
TandemQ:TotalSystemTime	30	18.132	0.5
TandemQ:Station1:R:NumBusy	30	0.671	0.008
TandemQ:Station1:R:Util	30	0.671	0.008
TandemQ:Station1:NS	30	2.031	0.088
TandemQ:Station1:StationTime	30	12.107	0.483
TandemQ:Station1:Q:NumInQ	30	1.359	0.081
TandemQ:Station1:Q:TimeInQ	30	8.101	0.457
TandemQ:Station2:R:NumBusy	30	0.5	0.004
TandemQ:Station2:R:Util	30	0.5	0.004
TandemQ:Station2:NS	30	1.01	0.023
TandemQ:Station2:StationTime	30	6.029	0.135
TandemQ:Station2:Q:NumInQ	30	0.51	0.02
TandemQ:Station2:Q:TimeInQ	30	3.042	0.12
TandemQ:TotalProcessed	30	2512.667	17.41
TandemQ:Station1:NumProcessed	30	2512.7	17.535
TandemQ:Station2:NumProcessed	30	2512.667	17.41

4.6.4 Modeling with the Station Package

The ksl.modeling.station package has many options that can be utilized to model complex situations. This section discusses some of the options and offers some reasons and strategies for their application.

Imagine if the tandem queue system consisted of 100 stations. How might you model that situation? You would need to make 100 instances of the SingleQStation class. This could easily be accomplished in a for-loop which captures the instances into a list of stations. Then, the list could be iterated to assign the nextReceiver property of the station. That is, iterate the list and assign each station’s receiver to the next element in the list. This approach builds on the notion of directly connecting the receivers as illustrated in the tandem queue example. However, there may be better approaches.

A better approach is to use the sending option that is attached to the QObject instance when the instance is created and let every created QObject instance follow their own sequence through the system. This can be accomplished by using an instance of the ReceiverSequence class.

The ReceiverSequence class sub-classes from the QObjectSender class. As previously mentioned senders implement the QObjectSenderIfc interface. That is, they know how or where to send the QObject instance. The main variation between senders is the selection of the next QObjectReceiverIfc instance to receive the QObject instance. The QObjectSender class is an abstract base class that requires the implementation of the selectNextReceiver() function.

abstract class QObjectSender() :  QObjectSenderIfc {

    /**
     *  Can be used to supply logic if the iterator does not have
     *  more receivers.
     */
    private var noNextReceiverHandler: ((ModelElement.QObject) -> Unit)? = null

    fun noNextReceiverHandler(fn: ((ModelElement.QObject) -> Unit)?){
        noNextReceiverHandler = fn
    }

    abstract fun selectNextReceiver(): QObjectReceiverIfc?

    final override fun send(qObject: ModelElement.QObject) {
        val selected = selectNextReceiver()
        if (selected != null) {
            beforeSendingAction?.action(selected, qObject)
            selected.receive(qObject)
            afterSendingAction?.action(selected, qObject)
        } else {
            noNextReceiverHandler?.invoke(qObject)
        }
    }

    private var beforeSendingAction: SendingActionIfc? = null

    fun beforeSendingAction(action : SendingActionIfc){
        beforeSendingAction = action
    }

    private var afterSendingAction: SendingActionIfc? = null

    fun afterSendingAction(action : SendingActionIfc){
        afterSendingAction = action
    }
}

The QObjectSender class defines how QObject instances will be sent and allows for the handling of a receiver not being selected. In addition, you can use lambda expressions to add actions prior to and after sending the QObject instance. Let’s review the implementation of the ReceiverSequence class.

class ReceiverSequence(
    private val receiverItr: ListIterator<QObjectReceiverIfc>
) : QObjectSender() {

    override fun selectNextReceiver(): QObjectReceiverIfc? {
        return if (receiverItr.hasNext()){
            receiverItr.next()
        } else {
            null
        }
    }
}

As can be seen in the code for the ReceiverSequence class, a list iterator is used and checked. If the next receiver is found, it is returned and the QObject instance will be sent to the receiver. So imagine that you have a list of QObjectReceiverIfc instances, in a list called stations, then the following code could be implemented to assign the sequence to the QObject instance when it is created.

    private fun arrivalEvent(generator: EventGenerator){
        val itr = stations.listIterator()
        val customer = QObject()
        customer.sender = ReceiverSequence(itr)
        customer.sender.send(customer)
    }

The sender will cause the customer to go to the first receiver presented by the iterator and then after that each station will automatically cause the customer to continue using the iterator until there are no more receivers. The trick is handling the last receiver, which could easily be a receiver like the ExitSystem receiver used in the tandem queue implementation that does not cause further use of the iterator. This approach is very flexible. For example, imagine different types of customers being assigned different iterators (based on different lists of stations). The approach would allow stations to be visited multiple times, skipped, etc. all based on the ordering of stations in a list and the resulting iterators from those lists.

As previously mentioned, there are actually 3 mechanisms (or options) for sending QObject instances: 1) directly specifying a receiver (illustrated in the tandem queue model), 2) attaching a sender to the QObject instance (discussed in this section), and 3) specifying a sender for the station. We have already discussed options 1 and 2. For option 3, while it is possible that every station may have its own unique instance of a sender (i.e. a QObjectSenderIfc instance), a more plausible approach would be that the stations share a global sender. In this approach you simply defer the sending functionality to some complex object at the system level that determines where to send the QObject instance next. Since system control logic may take into account the entire state of the system in order to optimally route the workload among the stations, this approach seems extremely useful.

In reviewing Figure 4.16 you may also notice the ActivityStation, the TwoWayByChanceSender, and NWayByChanceSender classes. The ActivityStation class models a station that does not have a resource by implementing a simple scheduled delay for a specified activity time. The TwoWayByChanceSender class provides probabilistic routing between two specified receivers according to a Bernoulli random variable. The NWayByChanceSender class provides probabilistic routing from a list of receivers according to a discrete empirical distribution. The TwoWayByChanceSender and NWayByChanceSender classes are special in that they behave as both senders and receivers of QObject instances. That is, they implement both the QObjectReceiverIfc interface and the QObjectSenderIfc interface. Essentially, their receiving action is to immediately execute the sending action. This dual behavior allows them to be used in any of the three options for sending QObject instances.

As one final point of discussion, the ability to attach Kotlin lambda expressions within the stations package should not be under appreciated. Let’s suppose you were simulating a system where parts might need to repeatedly visit a particular station and you wanted to count the number of times that the part visited the station in order to invoke control logic based on the count. How might you model this situation using stations? The first task would be to subclass QObject to have a sub-type that had an attribute to hold the visit count.

private inner class Part(var visitCount: Int = 0) : QObject()

Now, suppose the station for which we wanted to track the visits was the drilling station (called drilling). Then, when setting up the initialization logic within the init{} block we can attach a lambda expression to the drilling station and ensure that every time that the station is visited, the part increments the visitation count. The code might look something like this:

    init {
        myArrivalGenerator.generatorAction { drilling.receive(Part()) }
        drilling.exitAction { (it as Part).visitCount++ }
        drilling.nextReceiver(grinding)
        // etc.
        grinding.nextReceiver(exit)
    }

Since the GeneratorActionIfc is a SAM functional interface, the code takes advantage of this by supplying the generation logic as a lambda expression. In addition, the exit action for the drilling station is specified as a lambda expression. In this case, the reference object of the lambda is cast to an instance of the Part class and then the visit count attribute is incremented. This code illustrates a single line lambda; however, there is no limitation on the number of lines of the lambda expression. Also, if you do not like lambda expressions, you can simply make an inner class that implements the ExitActionIfc interface and use the syntax which best matches your programming style.

Using these constructs, the KSL can model very large and complex queueing situations using the relatively simple framework provided by the ksl.modeling.station package. The next chapter will present many ways in which you can capture and use the simulation results to make decisions based on the statistical results.