4.5 Enhancing the Drive Through Pharmacy Model
In this section, we re-implement the drive through pharmacy model to illustrate a few more KSL constructs.
Example 4.5 (Enhance Drive Through Pharmacy) Consider again the drive through pharmacy situation. Assume that customers arrive at a drive through pharmacy window according to a Poisson distribution with a mean of 10 per hour. The time that it takes the pharmacist to serve the customer is random and data has indicated that the time is well modeled with an exponential distribution with a mean of 3 minutes. Customers who arrive to the pharmacy are served in the order of arrival and enough space is available within the parking area of the adjacent grocery store to accommodate any waiting customers. For this situation, we are interested in estimating the following performance measures:
- Expected time spent waiting in the queue.
- Probability of having 0, 1, 2, 3, etc. in the queue upon arrival.
- The utilization of the pharmacist.
- The number of times that the pharmacist attempted to serve a customer.
- A histogram for the total time spent in the system.
The solution to this situation will involve five new KSL constructs.
SResource- To model the pharmacist as a resource and automatically collect resource statistics.Queue- To model the customer waiting line.QObject- To model the customers and facilitate statistical collection on waiting time in the queue.IntegerFrequencyResponse- To collect statistics on the number of customers waiting when another customer arrives.HistogramResponse- To collect a histogram on the system times of the customers.EventGenerator- To model the arrival pattern of the customers.
The purpose is to cover the basics of these classes for future modeling. The SResource class represents a simple resource that has a unchangeable capacity. The Queue and QObject classes facilitate the holding of entities within waiting lines or queues, while the EventGenerator class codifies the basics of generating events according to a repetitive pattern. We will start by expanding on the concept of a resource.
4.5.1 Modeling a Simple Resource
As we saw in the drive through pharmacy example, when the customer arrives they need the pharmacist in order to proceed. As noted in the activity diagram depicted in Figure 4.9, we denoted the pharmacist as a resource (circle) in the diagram. A resource is something that is needed by the objects (or entities) that experience the system’s activities. In the pharmacy example, the resource (pharmacist) was required to start the service activity, denoted with a arrow with the word “seize” in the activity diagram, pointing from the resource to the start of the activity. After the activity is completed, there is a corresponding arrow labeled “release” pointing from the end of the activity back to the resource. This arrow denotes the returning of the used resource units back to the pool of available units.
For the purposes of this situation, we are going to represent the concept of a simple resource with the aptly named SResource class (for simple resource). Let’s take a look at how the KSL represents a simple resource.

Figure 4.11: A Simple Resource Class
A resource has a capacity that represents the maximum number of units that it can have available at any time. When a resource is seized some amount of units become busy (or allocated). When the units are no longer needed, they are released. If we let \(A(t)\) be the number of available units, \(B(t)\) be the number of busy units and \(c\) be the capacity of the resource, we have that \(c = A(t) + B(t)\) or \(A(t) = c - B(t)\). A resource is considered busy if \(B(t) > 0\). That is, a resource is busy if some units are allocated. A resource is considered idle if no units are busy. That is, \(B(t) = 0\), which implies that \(A(t) = c\).
If the number of available units of a resource are unable to meet the number of units required by a “customer”, then we need to decide what to do. To simplify this modeling, we are going to assume two things 1) customers only request 1 unit of the resource at a time, and 2) if the request cannot be immediately supplied the customer will wait in an associated queue. These latter two assumptions are essentially what we have previously assumed in the modeling of the pharmacy situation. Modeling often requires the use of simplifying assumptions.
The SResource class of Figure 4.11 has functions seize() and release() which take (seize) and return (release) units of the resource. It also has properties (busy and idle) that indicate if the resource is busy or idle, respectively. In addition, the property numBusyUnits represents \(B(t)\) and the property numAvailableUnits represents \(A(t)\). For convenience, the hasAvailableUnits property indicates if the resource has units that can be seized. Finally, the number of times the resource is seized and released are tabulated. The main performance measures are time weighted response variables for tabulating the time-average number of busy units and the time-average instantaneous utilization of the resource. Instantaneous utilization, \(U(t)\) is governed by tracking \(U(t) = B(t)/c\).
4.5.2 Modeling a Queue with Statistical Collection
The Queue class, is used to model waiting lines. The Queue class is a sub-class
of ModelElement that is able to hold instances of the class QObject and
will automatically collect statistics on the number in the queue and the
time spent in the queue.
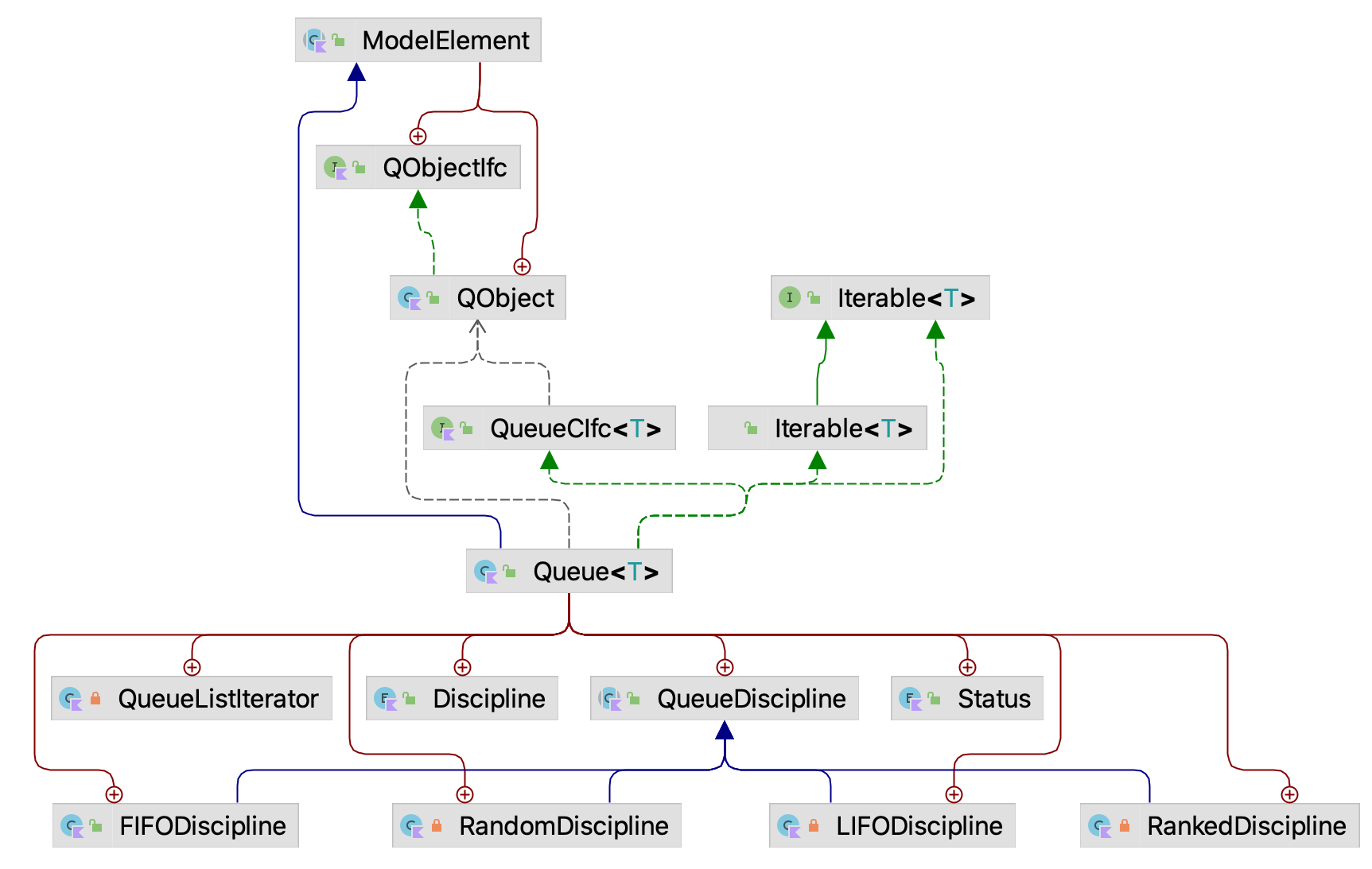
Figure 4.12: Overview of Classes Related to Queue and QObject
Figure 4.12 illustrates the classes involved when using the Queue and QObject classes. The first thing to note is that QObject is an inner class of ModelElement. This permits subclasses of ModelElement to create instances of QObject that have access to all the architecture of the model but are not model elements. That is, instances of QObject are transitory and are not added to the model element hierarchy that has been previously described. Users create QObject instances, use them to model elements of interest in the system that may experience waiting and then allow the Kotlin garbage collector to deallocate the memory associated with the instances. In Figure 4.12, we also see the class Queue<T: ModelElement.QObject is a sub-class of ModelElement that is parameterized by sub-types of QObject. Thus, users can develop sub-classes fo QObject and still use Queue to hold and collect statistics on those object instances. As noted in the figure, Queue also implements iterable. The last item to notice from Figure 4.12 is that queues can be governed by four basic queue disciplines: FIFO, LIFO, random, and ranked. In the case of a ranked queue, the queue is ordered by the priority property of QObject. The KSL permits the changing of the queue discipline during the simulation. The default queue discipline is FIFO.
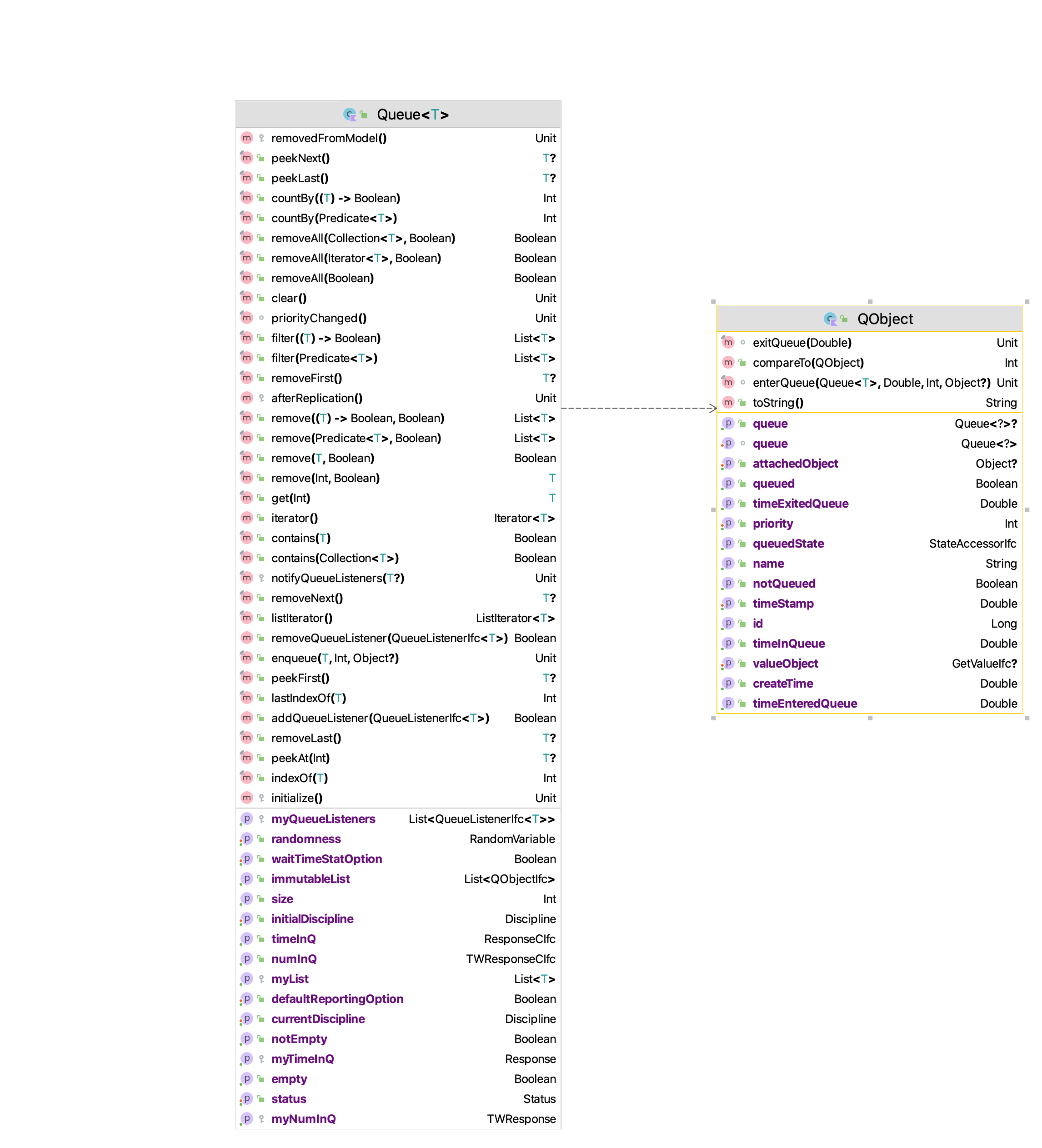
Figure 4.13: Properties and Methods of Queue and QObject
Figure 4.13 presents the properties and methods of the Queue and QObject classes. Here we can see that the Queue class has some standard methods for inserting and removing QObject instances. For the purposes of this chapter, the most noteworthy of these are:
fun enqueue(qObject: T, priority: Int = qObject.priority, obj: Any? = qObject.attachedObject)
fun peekNext(): T?
fun removeNext(): T? The enqueue method places QObject instances into the queue using the supplied priority. It also allows the user to attach an instance of Any to the QObject instance. The peekNext method provides a reference to the next QObject to be removed according the specified queue discipline and the removeNext method will remove the next QObject instance. During the enqueue and removal processes statistics are tabulated on the number of items in the queue and how much time the items spent in the queue. These responses are available via the timeInQ and numInQ properties. We will see how to use these classes within the revised pharmacy model. Before proceeding with reviewing the implementation, let us examine the EventGenerator class.
4.5.3 Modeling a Repeating Event Pattern
The EventGenerator class allows for the periodic generation of events
similar to that achieved by “CREATE” modules in other simulation languages.
This class works in conjunction with the GeneratorActionIfc
interface, which is used to listen and react to the events that are
generated by this class. Users of the class can supply an instance of an
GeneratorActionIfc to provide the actions that take place when
the event occurs. Alternatively, if no GeneratorActionIfc is
supplied, by default the generator(event: KSLEvent) method of this class
will be called when the event occurs. Thus, sub-classes can simply
override this method to provide behavior for when the event occurs. If
no instance of an GeneratorActionIfc instance is supplied and the
generate() method is not overridden, then the events will still occur;
however, no meaningful actions will take place. The key input parameters
to the EventGenerator include:
- time until the first event
-
This parameter is specified with an object that implements the
RandomIfc.It should be used to represent a positive real value that represents the time after time 0.0 for the first event to occur. If this parameter is not supplied, then the first event occurs at time 0.0. This parameter is specified by theinitialTimeUntilFirstEventproperty. - time between events
-
This parameter is specified with an object that implements the
RandomIfc.It should be used to represent a positive real value that represents the time between events. If this parameter is not supplied, then the time between events is positive infinity. This parameter is specified by theinitialTimeBetweenEventsproperty. - time until last event
-
This parameter is specified with an object that implements the
RandomIfc.It should be used to represent a positive real value that represents the time that the generator should stop generating. When the generator is created, this variable is used to set the ending time of the generator. Each time an event is to be scheduled the ending time is checked. If the time of the next event is past this time, then the generator is turned off and the event will not be scheduled. The default is positive infinity. This parameter is specified by theinitialEndingTimeproperty. - maximum number of events
-
A value of type long that supplies the maximum number of events to generate. Each time an event is to be scheduled, the maximum number of events is checked. If the maximum has been reached, then the generator is turned off. The default is
Long.MAX_VALUE. This parameter cannot beLong.MAX_VALUEwhen the time until next always returns a value of 0.0. This is specified by theinitialMaximumNumberOfEventsproperty. - the generator action
-
This parameter can be used to supply an instance of
GeneratorActionIfcinterface to supply logic to occur when the event occurs.
The most common use case for an EventGenerator is very similar to a
compound Poisson process. The EventGenerator is setup to run
with a time between events until the simulation completes; however,
there are a number of other possibilities that are facilitated through
various methods associated with the EventGenerator class. The first
possibility is to sub-class the EventGenerator to make a custom
generator for objects of a specific class. To facilitate this the user
need only over ride the generate() method that is part of the
EventGenerator class. For example, you could design classes to create
customers, parts, trucks, demands, etc.
In addition to customization through sub-classes, there are a number of
useful methods that are available for controlling the EventGenerator.
turnOffGenerator()-
This method allows an
EventGeneratorto be turned off. The next scheduled generation event will not occur. This method will cancel a previously scheduled generation event if one exists. No future events will be scheduled after turning off the generator. Once the generator has been turned off, it cannot be restarted until the next replication. turnOnGenerator(t: GetValueIfc)-
If the generator was not started upon initialization at the beginning of a replication, then this method can be used to start the generator. The generator will be started \(t\) time units after the call. If this method is used when the generator is already started it does nothing. If this method is used after the generator is done it does nothing. If this method is used after the generator has been suspended it does nothing. In other words, if the generator is already on, this method does nothing.
suspend()-
This method suspends the event generation pattern. The generator is still on, but the generation of events is suspended. The next scheduled generation event is canceled.
resume()-
If the generator is suspended then this method causes the event generator to proceed with the event generation pattern by scheduling a new event according to the time between event distribution.
suspended-
Checks if the generator is suspended.
done-
Checks if the generator has been turned off. The generator can be turned off via the
turnOffGenerator()method or it may turn off when it has reached its time until last event or if the maximum number of events is reached. As previously noted, once a generator has been turned off, it cannot be turned on again within the same replication.
In considering these methods, a generator can turn itself off (as an
action) within or caused by the code within its generate()method or in
the supplied GeneratorActionIfc interface. It might also
suspend() itself in a similar manner. Of course, a class that has a
reference to the generator may also turn it off or suspend it. To resume
a suspended event generator, it is necessary to schedule an event whose
action invokes the resume() method. Obviously, this can be within a
sub-class of EventGenerator or within another class that has a reference
to the event generator.
4.5.4 Collecting More Detailed Statistics
Example 4.5 also has requirements to collect the probability associated with the number of customers in the queue when a new customer arrives and for collecting a histogram for the time spent in the system for the customers. These requirements will be implemented using the IntegerFrequencyResponse and HistogramResponse classes. The IntegerFrequencyResponse and HistogramResponse classes are implementations of the IntegerFrequency and Histogram classes described in Section 3.1.2. The HistogramResponse class tabulates counts and frequencies of observed data over a set of contiguous intervals. The IntegerFrequencyResponse class will also tabulate count frequencies when the values are only integers. Both of these classes are designed to be used withing a KSL discrete-event simulation. One item to note is that both classes will collect statistics from within a warm up period (see Section 5.6.1). In fact, these classes report statistics based on observations from every replication of the simulation.
4.5.5 Implementing the Enhanced Pharmacy Model
Now we are ready to review the revised implementation of the drive through pharmacy model which puts the previously described classes into action. Only portions of the code are illustrated here. For full details see the example files in the ksl.examples.book.chapter4 package. To declare an instance of the SResource class, the following pattern is recommended:
private val myPharmacists: SResource = SResource(
parent = this,
capacity = numServers,
name = "${this.name}:Pharmacists"
)
val resource: SResourceCIfc
get() = myPharmacistsNotice that the name of the parent model element is used as a prefix for the name of the resource to ensure that the name for the pharmacist is unique. Also note that exposure to useful components of SResource are made possible via the SResourceCIfc interface. Through this interface the initial capacity can be changed, the state of the resource can be accessed, and access to the statistical collection of the number busy and utilization are available.
To collect the histogram and integer frequency statistics, we can use the following declarations.
private val mySysTime: Response = Response(parent = this, name = "${this.name}:SystemTime")
val systemTime: ResponseCIfc
get() = mySysTime
private val mySysTimeHistogram: HistogramResponse = HistogramResponse(theResponse = mySysTime)
val systemTimeHistogram: HistogramIfc
get() = mySysTimeHistogram.histogram
private val myInQ = IntegerFrequencyResponse(parent = this, name = "${this.name}:NQUponArrival")The HistogramResponse class requires an instance of the Response class. In this case, we supply a reference the response that is used to collect the system times for the customers. The reference is used internally to observe the response. The instance of the IntegerFrequencyResponse class will be used within the arrival logic to observe the number of customers in the queue when the customer arrives.
To declare an instance of the Queue class, we use the following code.
private val myWaitingQ: Queue<QObject> = Queue(parent = this, name = "${this.name}:PharmacyQ")
val waitingQ: QueueCIfc<QObject>
get() = myWaitingQNotice how we also declare a public property that exposes part of the queue functionality, especially related to getting access to the statistical responses.
We can create and use an instance of EventGenerator with the following code. We see that the event generator uses a reference to the functional interface GeneratorActionIfc. This is accomplished with the this::arrival syntax, which provides a reference to the arrival function shown in the code.
In addition, the time between arrivals random variable is supplied for both the time until the first event and the time between events. The initialize() method of the EventGenerator class ensures that the first event is scheduled automatically at the start of the simulation. In addition, the EventGenerator class continues rescheduling the arrivals according to the time between arrival pattern. As previously noted, this process can be suspended, resumed, and turned off if needed. An event generator can also be specified not to automatically start at time 0.
private val endServiceEvent = this::endOfService
private val ad = ExponentialRV(1.0, 1)
private val myArrivalGenerator: EventGenerator = EventGenerator(
parent = this, generateAction = this::arrival, timeUntilFirstRV = ad, timeBtwEventsRV = ad
)
val arrivalGenerator: EventGeneratorRVCIfc
get() = myArrivalGenerator
private fun arrival(generator: EventGeneratorIfc) {
myNS.increment() // new customer arrived
myInQ.value = myWaitingQ.numInQ.value.toInt()
val arrivingCustomer = QObject()
myWaitingQ.enqueue(qObject = arrivingCustomer) // enqueue the newly arriving customer
if (myPharmacists.hasAvailableUnits) {
myPharmacists.seize()
val customer: QObject? = myWaitingQ.removeNext() //remove the next customer
// schedule end of service, include the customer as the event's message
schedule(eventAction = endServiceEvent, timeToEvent = myServiceRV, message = customer)
}
}In the code for arrivals, we also see the use of the Queue class (via the variable myWaitingQ) and the QObject class. On line 7 of the code, we see val arrivingCustomer = QObject() which creates an instance of QObject that represents the arriving customer. Then, using the enqueue method the customer is placed within the queue. This action is performed regardless of whether the customer has to wait to ensure that zero wait times are collected. Notice that on line 6, the IntegerFrequencyResponse instance is used to observe the number of customers in the queue upon arrival.
Then, in lines 9-14, we see that the number busy is checked against the number of pharmacists by using the hasAvailableUnits property of the SResource instance. If there are available pharmacists, then a unit of the pharmacist resource is seized, the next customer is removed from the queue, and the customer’s end of service action is scheduled. Notice how the schedule method is different from the previous implementation. In this implementation, the customer is attached to the KSLEvent instance and is held in the calendar with the event until the event is removed from the calendar and its execution commences. Let’s take a look at the revised end of service action.
private fun endOfService(event: KSLEvent<QObject>) {
myPharmacists.release()
if (!myWaitingQ.isEmpty) { // queue is not empty
myPharmacists.seize()
val customer: QObject? = myWaitingQ.removeNext() //remove the next customer
// schedule end of service
schedule(eventAction = endServiceEvent, timeToEvent = myServiceRV, message = customer)
}
departSystem(departingCustomer = event.message!!)
}
private fun departSystem(departingCustomer: QObject) {
mySysTime.value = (time - departingCustomer.createTime)
myNS.decrement() // customer left system
myNumCustomers.increment()
}Here we see the same basic logic as in the previous example, except in this case we can use the resource and the queue. First, a unit of the pharmacist is released. Then, the queue is checked to see if it is empty, if not, a unit of the pharmacist is seized and the next customer is removed. Then, the customer’s service is scheduled. We always handle the departing customer by grabbing it from the message attached to the event via the event.message property. This departing customer is sent to a private method that collects statistics on the customer. Notice two items. First, it is perfectly okay to call other methods from within the event routines. In fact, this is encouraged and can help organize your code.
Secondly, we are passing along the instance of QObject until it is no longer needed. In the departingSystem method, we get the current simulation time via the time property that is available to all model elements. This property represents the current simulation time. We then subtract off the time that the QObject was created by using the createTime property of the departing customer. This is assigned to the value property of an instance of Response called mySystemTime. This causes the system time of every departing customer to be collected and statistics reported. The process of collecting statistics on QObject instances is extremely common and works if you understand how to pass the QObject instance along via the KSLEvent instances.
There is another little tidbit that is occurring in the reference coded snippet. Earlier in the arrivals code snippet, you might not have noticed the following line of code:
For convenience, this line of code is capturing a functional reference to the endOfService method. The EventActionIfc interface is actually a functional interface, which allows functional references that contain the same signature to be used without having to implement the interface. This feature of Kotlin allows the functional reference to private fun endOfService(event: KSLEvent<QObject>) to serve as a parameter to the schedule() method. This alleviates the need to implement an inner class that extends the EventActionIfc interface. A similar strategy was used for the implementation of GeneratorActionIfc for use in the event generator, except in that case we did not declare a variable to hold the reference to the function. The style that you employ can be based on your own personal preferences.
The results of running the simulation match the previously reported results.
Half-Width Statistical Summary Report - Confidence Level (95.000)%
Name Count Average Half-Width
----------------------------------------------------------------------------
Pharmacy:Pharmacists:NumBusy 30 0.5035 0.0060
Pharmacy:Pharmacists:Util 30 0.5035 0.0060
Pharmacy:NumInSystem 30 1.0060 0.0271
Pharmacy:SystemTime 30 6.0001 0.1441
Pharmacy:PharmacyQ:NumInQ 30 0.5025 0.0222
Pharmacy:PharmacyQ:TimeInQ 30 2.9961 0.1235
SysTime >= 4 minutes 30 0.5136 0.0071
Pharmacy:Pharmacists:SeizeCount 30 2513.4000 17.6653
Pharmacy:NumServed 30 2513.2667 17.6883
----------------------------------------------------------------------------In the results, we see the system time and the queueing time reported. The response called Pharmacy:Pharmacists:SeizeCount reports the number of times that the pharmacist resource was seized. Notice that its value is very close to the number of customers served. The difference is due to the fact that seizing occurs before the service time and the number served is collected when the customer departs. Notice also that the use of the SResource class causes statistics for the number busy and the utilization to be reported. The statistics are exactly the same in this situation because there is only one pharmacist.
We also see a statistic called SysTime > 4.0 minutes. This was captured by using an IndicatorResponse, which is a subclass of Response that allows the user to specify a function that results in boolean expression and an instance of a Response to observe. The expression is collected as a 1.0 for true and 0.0 for false. In this example, we are observing the response called mySysTime.
private val mySTGT4: IndicatorResponse = IndicatorResponse(
predicate = { x -> x >= 4.0 },
observedResponse = mySysTime,
name = "SysTime >= 4 minutes"
)
val probSystemTimeGT4Minutes: ResponseCIfc
get() = mySTGT4This allow a probability to be estimated. In this case, we estimated the probability that a customer’s system time was more than 4.0 minutes.
In addition, the call to the print() function will provide the histogram and integer frequency results in the console.
Pharmacy:SystemTime:Histogram
binNum binLabel binLowerLimit binUpperLimit binCount cumCount proportion cumProportion
0 1 1 [ 0.00, 4.00) 0.0 4.0 48589.0 48589.0 0.485448 0.485448
1 2 2 [ 4.00, 8.00) 4.0 8.0 24974.0 73563.0 0.249513 0.734961
2 3 3 [ 8.00,12.00) 8.0 12.0 12711.0 86274.0 0.126994 0.861956
3 4 4 [12.00,16.00) 12.0 16.0 6658.0 92932.0 0.066519 0.928475
4 5 5 [16.00,20.00) 16.0 20.0 3441.0 96373.0 0.034379 0.962854
5 6 6 [20.00,24.00) 20.0 24.0 1911.0 98284.0 0.019093 0.981946
6 7 7 [24.00,28.00) 24.0 28.0 985.0 99269.0 0.009841 0.991787
7 8 8 [28.00,32.00) 28.0 32.0 458.0 99727.0 0.004576 0.996363
8 9 9 [32.00,36.00) 32.0 36.0 221.0 99948.0 0.002208 0.998571
9 10 10 [36.00,40.00) 36.0 40.0 143.0 100091.0 0.001429 1.000000The integer frequency tabulation shows the number of customers in queue upon the arrival of a new customer. We can see that there is about a 0.75 chance that a customer arrives to an empty queue.
Pharmacy:NQUponArrival
cellLabel value count cum_count proportion cumProportion
0 label: 0 0 74944.0 74944.0 0.747243 0.747243
1 label: 1 1 12615.0 87559.0 0.125780 0.873023
2 label: 2 2 6303.0 93862.0 0.062845 0.935869
3 label: 3 3 3178.0 97040.0 0.031687 0.967555
4 label: 4 4 1581.0 98621.0 0.015764 0.983319
5 label: 5 5 765.0 99386.0 0.007628 0.990947
6 label: 6 6 417.0 99803.0 0.004158 0.995104
7 label: 7 7 235.0 100038.0 0.002343 0.997448
8 label: 8 8 136.0 100174.0 0.001356 0.998804
9 label: 9 9 72.0 100246.0 0.000718 0.999521
10 label: 10 10 27.0 100273.0 0.000269 0.999791
11 label: 11 11 13.0 100286.0 0.000130 0.999920
12 label: 12 12 5.0 100291.0 0.000050 0.999970
13 label: 13 13 3.0 100294.0 0.000030 1.000000The IntegerFrequencyResponse and HistogramResponse also facilitate the plotting of their results. See the documentation for further details.