9.1 Bootstrap Methods
Bootstrapping is a statistical procedure that resamples from a sample to create many simulated samples. Although there are some parametric bootstrapping approaches, bootstrapping is generally considered a non-parametric Monte Carlo method that estimates characteristics of a population by resampling. The samples from the original sample are used to make inferences about the population and about the statistical properties computed from the original sample. The intuitions associated with bootstrapping come from a deep understanding of what it means to sample.
The concepts of estimation theory presented in Section 3.3 of Chapter 3 are based on having a random sample. Let \(x_{i}\) represent the \(i^{th}\) observations in a sample, \(x_{1}, x_{2},\cdots,x_{n}\) of size \(n\). Represent the random variables in the sample as \(X_{1}, X_{2},\cdots,X_{n}\). The random variables form a random sample, if 1) the \(X_{i}\) are independent random variables and 2) every \(X_{i}\) has the same probability distribution. We assume that the random sample comes from some population. In statistical estimation theory, a population is the complete set of items from which we desire to make inferences. We assume that the population represents a set of things that have one or more characteristics in common. A population may be finite or infinite. In the case of a finite population, the size of the population may be so large or it may be too time consuming or costly to enumerate all elements of the population. However, conceptually, for a finite population, we can assign an integer to each element and thus count the elements and the final number of elements will be finite number. In the case of an infinite population, the definition of the underlying characteristics of the items makes enumeration impossible. That is, we cannot represent the number of elements in the population with a finite integer.
The concept of a finite population and an infinite population is sometimes confused with the concepts of discrete and continuous random variables. A continuous random variable has (by the underlying characteristics of its elements) an infinite population. For example, consider a random variable representing the time of arrival, \(A_i\). Since the underlying quantity is time, we note that time (conceptually) is a continuous thing, it is infinitely divisible and has no limit (at least based on our current understand of physics). A discrete random variable can have either a finite or an infinite population. Consider for example, the number of heads within 100 flips of a coin. This random variable is governed by a binomial distribution, and can take on any of the values \(0, 1, 2, \cdots, n\) where \(n=100\), the (finite) number of trials. In this case, the population (set of possible values) is finite. However, now consider a geometric random variable. The set of possible values for a geometric random variable \(0, 1, 2, \cdots,\). That is, we could (in theory, however unlikely), wait an “infinite” amount of time until the first success occurs. The population of a geometric random variable (although discrete) is infinite.
Sampling theory and statistical inference are applied to situations involving both finite and infinite populations. In many of the cases of finite populations, it is impractical to enumerate the items. In the case of an infinite population, it is impossible to enumerate the items. Thus, we are forced to sample from the population. That is, select through some mechanism, a subset of the elements of the population. If we select the elements in the sample in such a manner that each element in the sample is equally likely to have come from the population, then we have a random sample.
In essence, bootstrapping takes this notion one step further. In bootstrapping, we assume that some original random sample is essentially the population. That is, we assume that a random sample, if large enough, can act as the actual population. Thus, sampling from the sample is, in essence, sampling from the population. This sampling and resampling process can provide information about the properties of statistical quantities computed from the original sample. Bootstrapping assumes that if the original sample is representative of the true population, then statistics generated from samples of the original sample of the population provide observations of the sampling distribution.
Let’s formalize these concepts with some notation and an informal overview of some of the theory associated with bootstrapping. The interested reader should refer to (Efron and Tibshirani 1986), (Efron and Tibshirani 1994), and (Davison AC 1997) for more detailed treatments. This presentation follows somewhat the tutorial (Wehrens and Buydens 2000). Let the cumulative distribution function of some random variable, \(X\), be denoted as \(F.\) Let \(x_{1}, x_{2},\cdots,x_{n}\) be a set of observed values of \(X\) from \(F.\) Suppose that there is some unknown parameter \(\theta\) that represents a population parameter of interest. For example, \(\theta\) might be the mean, median, correlation, etc. Suppose that \(\theta\) can be expressed or computed by some function \(t(\cdot)\) applied to the distribution function \(F\). That is, we can write \(\theta = t(F)\). For example, in the case of the population mean, \(E[X] =\theta\), \(t(\cdot)\) is the expectation function such that \(\theta = \int xdF(x)\).
In general, because the underlying probabilistic description of the population may not be known, we usually do not know \(F\). However, we are able to sample (through some mechanism) observations \(\vec{x}=(x_{1}, x_{2},\cdots,x_{n})\) from \(F\) via the random variable \(X\). This sample represents the empirical distribution, \(F_n(x)\), of \(F\). That is, \(F_n(x)\) is an estimate of \(F\).
We can either use \(F_n(x)\) to estimate \(\theta\) or use some function \(u(\cdot)\) applied to the sample to estimate \(\theta\). That is, we can formulate an estimator, \(\hat{\theta} = t(F_n) = u(\vec{x})\). For example in the case of the population mean, \(E[X] =\theta\), \(u(\cdot)\) is the sample mean, \(\bar{X}=\frac{1}{n}\sum_i^n X_i\). In bootstrapping, this equivalence is called the plug-in principle. As we will see, bootstrapping makes a more explicit use of the empirical distribution, \(F_n\).
Since we have that \((x_{1}, x_{2},\cdots,x_{n})\) is a set of observed values of \(X\) from \(F\), let’s define \(\vec{x}^{*}=(x^{*}_{1}, x^{*}_{2},\cdots,x^{*}_{n})\) as a set of observations from \(F_n\). That is, define \(X^{*}\) to be a possible observation selected at random from \((x_{1}, x_{2},\cdots,x_{n})\). Thus, \(F_n(x) = P(X^{*}=x_i)= 1/n\) for \(i=1,2,\cdots, n\). Let \(\vec{X}^{*}=(X^{*}_{1}, X^{*}_{2},\cdots,X^{*}_{n})\) be a random sample of size \(n\) from \(P(X^{*}=x_i)\). Then, the random variables \((X^{*}_{1}, X^{*}_{2},...X^{*}_{n})\) are independent and uniformly distributed over the set \((x_{1}, x_{2},\cdots, x_{n})\). Notice that values within \((x^{*}_{1}, x^{*}_{2},\cdots,x^{*}_{n})\) may be repeated because the sampling is done with replacement (to ensure that they are uniformly likely). Note also that we can form as many samples \((x^{*}_{1}, x^{*}_{2},\cdots,x^{*}_{n})\) as we want by repeating the sampling procedure from \(F_n\).
The empirical distribution, \(F_n(x)\), is an estimator for \(F(x)\) and it can be shown that \(F_n\) is a sufficient statistic for \(F\). To summarize, \(F\) yields random variables \(X\) of which we have a sample, which yields \(F_n\). When we sample from \(F_n\), we get random variables \(X^{*}\). These samples from \(F_n\) also have an empirical cumulative distribution function (ECDF). Let’s denote the ECDF of \(F_n\) as \(F^{*}_n\). Thus, a statistic formed from \((x^{*}_{1}, x^{*}_{2},\cdots,x^{*}_{n})\) will be a possible statistic computed on \((X_{1}, X_{2},\cdots,X_{n})\). Since a statistic computed from \((x^{*}_{1}, x^{*}_{2},\cdots,x^{*}_{n})\) yields a possible statistic computed on \((X_{1}, X_{2},\cdots,X_{n})\), these are possible observations from the sampling distribution of the estimator. This allows for the estimation of some parameter \(\theta\) of \(F(x)\) and the variability of the estimator by resampling. This is the basis of the bootstrapping principle.
We call the samples \((x^{*}_{1}, x^{*}_{2},\cdots,x^{*}_{n})\) bootstrap samples. Let \(x^{*(b)}\) be the \(b^{th}\) bootstrap sample from \(F_n(x)\), with \(b=1,2,\cdots,B\), where \(B\) is the number of bootstrap samples. Let \(\hat{\theta}\) be some estimator of \(\theta\) and let \(\hat{\theta}^{*}_{b}\) be an observation of \(\hat{\theta}\) based on the \(b^{th}\) bootstrap sample, \(x^{*(b)}\). The quantities, \(\hat{\theta}^{*}_{b}\) for \(b=1,2,\cdots,B\) are called the bootstrap replicates (of the estimator).
The bootstrap estimate of the sampling distribution of \(\hat{\theta}^{*}_{b}\), \(F_{\hat{\theta}^{*}_{b}}(\cdot)\) is the empirical distribution of \((\theta^{*}_{1}, \theta^{*}_{2},\cdots,\theta^{*}_{n})\). Thus, \(F_{\hat{\theta}^{*}_{b}}(\cdot)\) provides information on the sampling distribution of \(\hat{\theta}\). The quality of the information depends entirely on the quality of the original sample \((x_{1}, x_{2},\cdots,x_{n})\) of \(X\) from \(F\). Therefore, \(\hat{\theta}\) is a statistic computed from the original sample, and \(\hat{\theta}^{*}\) is a statistic computed from the resample. The bootstrap principle assumes that \(F^{*}\approx F\) and the variation in \(\hat{\theta}\) is well approximated by the variation in \(\hat{\theta}^{*}\).
If the bootstrap principle holds, then we can use the bootstrapping process to develop an estimate of the standard error of our estimator. We have an estimator, \(\hat{\theta}\). It has some variance, \(var(\hat{\theta})\) and standard deviation, \(\sqrt{var(\hat{\theta})}\). This quantity is called the standard error of the estimator. That is, \(se(\hat{\theta}) = \sqrt{var(\hat{\theta})}\). The bootstrap estimator of the standard error of the estimator,\(\hat{\theta}\), is:
\[ \widehat{se(\hat{\theta})} = \sqrt{\frac{1}{B-1}\sum_{b=1}^{B}\big(\hat{\theta}^{*}_{b} - \bar{\hat{\theta^{*}}} \big)^2} \] where the quantity, \(\bar{\hat{\theta^{*}}}\), is the average over the computed bootstrap estimates of the estimator:
\[ \bar{\hat{\theta^{*}}} =\frac{1}{B}\sum_{b=1}^{B}\hat{\theta}^{*}_{b} \]
As you can see, the bootstrap estimator for the standard error of the estimator, \(\widehat{se(\hat{\theta})}\), is simply the sample standard deviation of the bootstrap replicates.
The bootstrapping process not only provides information about the standard error of the estimator, \(\hat{\theta}\), it can also provide information about the bias of the estimator. If \(\hat{\theta}\) is an unbiased estimator of \(\theta\) then \(E[\hat{\theta}] = \theta\). Thus, the bias of an estimator, \(\hat{\theta}\), for \(\theta\) is:
\[ bias(\hat{\theta}) = E[\hat{\theta} - \theta] = E[\hat{\theta}] - \theta \] To estimate the bias, the bootstep process uses the bootstrap replicates of \(\hat{\theta}^{*}_{b}\) to estimate the sampling distribution of \(\hat{\theta}\) to get:
\[ \widehat{bias}(\hat{\theta}) = \bar{\hat{\theta^{*}}} - \hat{\theta} \] where \(\hat{\theta}\) is the estimate of \(\theta\) computed from the original sample,\((x_{1}, x_{2},.\cdots,x_{n})\). The bias and standard error of the estimator provide information about the accuracy and precision of the estimator. We can also provide confidence intervals for the estimator based on the bootstrapping process.
To derive confidence intervals from the bootstrapping process consider the probability distribution associated with \(\hat{\theta} - \theta\). Suppose \(\gamma_{\alpha}\) denotes the \(\alpha\)-percentile of the distribution of \(\hat{\theta} - \theta\), then a confidence interval for \(\theta\) is based on the probability statement:
\[ P\Bigg( \gamma_{\alpha/2} \leq \hat{\theta} - \theta \leq \gamma_{1-\alpha/2}\Bigg) = 1-\alpha \] After rewriting this statement, we have an interval of the form:
\[ \hat{\theta}- \gamma_{1-\alpha/2} \leq \theta \leq \hat{\theta} - \gamma_{\alpha/2} \] Within the bootstrap literature a number of approaches have been developed that provide approximate confidence intervals based on the previously noted form. These include:
- standard normal bootstrap confidence interval (SNBCI)
- basic bootstrap confidence interval (BBCI)
- bootstrap percentile confidence interval (BPCI)
- bootstrap bias corrected and acceleration adjusted (BCa)
- bootstrap-t confidence interval (BTCI), sometimes called the percentile-t confidence interval
The standard normal bootstrap confidence interval is useful to consider first because of its simplicity; however, the quality of the confidence intervals can be poor unless its assumptions hold. Based on the central limit theorem, we know that if the estimator, \(\hat{\theta}\), is the sample average, then for large sample sizes, we have:
\[ Z = \frac{\hat{\theta}-E[\hat{\theta}]}{se(\hat{\theta})} \] with \(Z\approx N(0,1)\). Therefore if \(\hat{\theta}\) is unbiased, an approximate \(100\times(1-\alpha)\%\) confidence interval will have the form:
\[ \hat{\theta}- z_{1-\alpha/2} se(\hat{\theta}) \leq \theta \leq \hat{\theta} + z_{1-\alpha/2}se(\hat{\theta}) \] To apply bootstrapping to compute this interval, we simply estimate \(se(\hat{\theta})\) with the bootstrap estimator of the standard error of the estimator, \(\widehat{se(\hat{\theta})}\).
The basic bootstrap confidence interval (BBCI), is also relatively simple. This confidence interval assumes that the distribution of \(\hat{\theta} - \theta\) is approximately the same as \(\hat{\theta} - \theta^*\). Suppose that \(\hat{\theta}\) is an estimator for \(\theta\).
\[ \begin{aligned} 1-\alpha & \approx P\Bigg( \hat{\theta}^{*}_{\alpha/2} \leq \hat{\theta}^* \leq \hat{\theta}^{*}_{1-\alpha/2}\Bigg)\\ & = P\Bigg( \hat{\theta}^{*}_{\alpha/2} - \hat{\theta} \leq \hat{\theta}^{*} - \hat{\theta} \leq \hat{\theta}^{*}_{1-\alpha/2} - \hat{\theta}\Bigg)\\ & = P\Bigg( \hat{\theta} - \hat{\theta}^{*}_{\alpha/2} \geq \hat{\theta} - \hat{\theta}^{*} \geq \hat{\theta} - \hat{\theta}^{*}_{1-\alpha/2} \Bigg)\\ & \approx P\Bigg( \hat{\theta} - \hat{\theta}^{*}_{\alpha/2} \geq \theta - \hat{\theta} \geq \hat{\theta}-\hat{\theta}^{*}_{1-\alpha/2} \Bigg)\\ & = P\Bigg( 2\hat{\theta} - \hat{\theta}^{*}_{\alpha/2} \geq \theta \geq 2\hat{\theta}-\hat{\theta}^{*}_{1-\alpha/2} \Bigg)\\ \end{aligned} \]
Thus, we have the lower limit as \(L = 2\hat{\theta}-\hat{\theta}^{*}_{1-\alpha/2}\) and the upper limit as \(U = 2\hat{\theta} - \hat{\theta}^{*}_{\alpha/2}\). We can estimate \(\hat{\theta}^{*}_{\alpha/2}\) and \(\hat{\theta}^{*}_{1-\alpha/2}\) by the percentiles of the bootstrap replicates distribution, which yields a final BBCI approximate \(100\times(1-\alpha)\%\) confidence interval as:
\[ 2\hat{\theta}- \hat{\theta}^{*}_{1-\alpha/2} \leq \theta \leq 2\hat{\theta} -\hat{\theta}^{*}_{\alpha/2} \] where \(\theta^{*}_{p}\) is the \(p^{th}\) sample quantile from the empirical distribution of the bootstrap replicates.
The percentile bootstrap confidence interval (PBCI) uses the empirical distribution of the bootstrap replicates to estimate the quantiles for the sampling distribution of \(\hat{\theta}\). Suppose \((\theta^{*}_{1}, \theta^{*}_{2},\cdots,\theta^{*}_{n})\) are the bootstrap replicates of \(\hat{\theta}\). From the empirical distribution of \((\theta^{*}_{1}, \theta^{*}_{2},\cdots,\theta^{*}_{n})\) compute the \(\alpha/2\) quantile, say \(\theta^{*}_{\alpha/2}\) and the \(1-\alpha/2\) quantile, \(\theta^{*}_{1-\alpha/2}\). Then, approximate \(100\times(1-\alpha)\%\) PBCI confidence interval is:
\[ (\hat{\theta}^{*}_{1-\alpha/2}, \, \hat{\theta}^{*}_{\alpha/2}) \]
The bootstrap bias corrected and acceleration adjusted (BCa) interval modifies the percentile bootstrap confidence interval by correcting for bias and adjusting for possible skewness in the sampling distribution of the estimator. The theory and quality of this confidence interval is discussed in (Efron and Tibshirani 1994). An approximate \(100\times(1-\alpha)\%\) BCa confidence interval is \((\hat{\theta}^{*}_{\alpha_1}, \, \hat{\theta}^{*}_{\alpha_2})\) where \(\alpha_1\) and \(\alpha_2\) are defined as follows:
\[ \alpha_1 = \Phi\bigg( \hat{z}_0 + \frac{\hat{z}_0 + z_{\alpha/2}}{1-\hat{a}(\hat{z}_0 + z_{\alpha/2})}\bigg) \]
\[ \alpha_2 = \Phi\bigg( \hat{z}_0 + \frac{\hat{z}_0 + z_{1-\alpha/2}}{1-\hat{a}(\hat{z}_0 + z_{1-\alpha/2})}\bigg) \]
where \(z_p = \Phi^{-1}(p)\). The bias correction factor, \(z_0\), is given as follows.
\[ z_0 = \Phi^{-1}\bigg( \frac{1}{B}\sum_{b=1}^{B}I(\hat{\theta}^{*}_{b} < \hat{\theta})\bigg) \]
where \(I(\cdot)\) is an indicator function. The acceleration adjustment factor, \(\hat{a}\), is given as follows.
\[ \hat{a} = \frac{\sum_{i=1}^{n}\big( \bar{\theta}_{(\cdot)} - \theta_{(i)} \big)^3}{6\sum_{i=1}^{n}\bigg(\big( \bar{\theta}_{(\cdot)} - \theta_{(i)} \big)^2\bigg)^{3/2}} \] The quantity \(\bar{\theta}_{(\cdot)}\) is the mean of the estimates of the leave one out jackknife samples, with:
\[ \bar{\theta}_{(\cdot)} = \frac{1}{n}\sum_{i=1}^{n}\hat{\theta}_{(i)} \]
and \(\hat{\theta}_{(i)}\) is the \(i^{th}\) jackknife replicate. The jackknife replicates, \(\hat{\theta}_{(i)}\) for \(i=1,2,\cdots,n\) are computed by applying the estimator, \(\hat{\theta} = T_n(x)\) on the jackknife samples. A jackknife sample, \(\vec{x}_{(i)}\), is a subset of \((x_{1}, x_{2},\cdots, x_{n})\) that leaves out the \(i^{th}\) observation such that:
\[ \vec{x}_{(i)} =(x_{1}, \cdots,x_{i-1},x_{i+1},\cdots, x_{n}) \] Thus, \(\hat{\theta}_{(i)} = T_{n-1}(\vec{x}_{(i)})\) for \(i=1,2,\cdots,n\). Jackknifing is another form of resampling that is often applied to reduce the bias in an estimator. We will not discuss the theory of jackknifing in this text, but we will point out that the KSL has support for the approach.
The bootstrap-t (BTCI) provides an approximate confidence interval by considering the distribution of
\[ \frac{\hat{\theta}-\theta}{se(\hat{\theta})} \]
As we know from basic statistical theory, if \(\hat{\theta}\), is the sample average and the \(se(\hat{\theta})\) is estimated by the sample error when the observations are IID normal, then this ratio should have a student-t distribution. In the PTCI approach, does not assume a student-t distribution, but rather uses the bootstrap observations of:
\[ t^{*}_{b} = \frac{\hat{\theta}^{*}_{b}-\hat{\theta}}{\widehat{se}(\hat{\theta}^{*}_{b})} \]
Notice that \(\widehat{se}(\hat{\theta}^{*}_{b})\) is the standard error of the \(b^{th}\) bootstrap sample and that it may not have a closed form. If \(\hat{\theta}\), is the sample average, then we can use the sample standard error of the \(b^{th}\) bootstrap sample, \(\vec{x}^{*}_{b} = (x^{*}_{1}, x^{*}_{2},...x^{*}_{n})\).
In general for this approach, the reference distribution is formed from resamples from the bootstrap sample. As usual, suppose that \((x_{1}, x_{2},...x_{n})\) is the original sample. Then, the \(100 \times (1-\alpha)\%\) bootstrap t-interval is:
\[ \big( \hat{\theta} - t^{*}_{1-\alpha/2 }\widehat{se}(\hat{\theta}^{*}), \hat{\theta} - t^{*}_{\alpha/2 }\widehat{se}(\hat{\theta}^{*})\big) \]
We compute \(\widehat{se}(\hat{\theta}^{*})\), \(t^{*}_{\alpha/2 }\), and \(t^{*}_{1-\alpha/2 }\) as follows:
- Compute \(\hat{\theta}\) from \(\vec{x}=(x_{1}, x_{2},...x_{n})\)
- For \(b = 1 \; \text{to} \; B\)
- Sample from \(\vec{x}^{*}_{b}\) with replacement from \(\vec{x}\).
- Compute \(\theta^{*}_{b}\) from \(\vec{x}^{*}_{b}\).
- Estimate the standard error \(\widehat{se}(\hat{\theta}^{*}_b)\) from sampling from \(\vec{x}^{*}_{b}\). In the case of \(\hat{\theta}\) being the mean, then the standard error of the bootstrap sample can be directly computed, without sampling.
- Compute \[ t^{*}_b = \frac{\theta^{*}_{b}-\hat{\theta}}{\widehat{se}(\hat{\theta}^{*}_b)} \]
- The sample \((t^{*}_1, t^{*}_2, \cdots, t^{*}_B)\) is the reference distribution for the bootstrap t-statistic. From these observations, find \(t^{*}_{\alpha/2 }\), and \(t^{*}_{1-\alpha/2 }\).
- Compute \(\widehat{se}(\hat{\theta}^{*})\) as the sample standard deviation of the \(\theta^{*}_{b}\) for \(b=1,2,\cdots, B\)
- Compute the confidence intervals
\[ \big( \hat{\theta} - t^{*}_{1-\alpha/2 }\widehat{se}(\hat{\theta}^{*}), \hat{\theta} - t^{*}_{\alpha/2 }\widehat{se}(\hat{\theta}^{*})\big) \]
(Efron and Tibshirani 1986) discuss many of the characteristics of the different bootstrap confidence intervals. Of the five presented here, the bootstrap percentile confidence interval is often utilized; however, because the BCa essentially corrects for bias and skewness issues for the BPCI, we would recommend utilizing the BCa. The next recommended confidence interval would be the bootstrap-t; however, because it often requires an extra bootstrapping step to estimate \(\widehat{se}(\hat{\theta}^{*}_b)\) it can require a substantial amount of extra computation. Thus, the bootstrap-t has not found wide acceptance in practice, except in the case of when the estimator is the sample average.
9.1.1 Bootstrapping Using the KSL
In this section, we will explore how the KSL supports the application of bootstrapping. First, we will illustrate how to do bootstrapping using basic KSL constructs. This is intended to illustrate the overall bootstrapping process. Then we will discuss KSL constructs that encapsulate the bootstrapping process within classes. In essence, bootstrapping is just sampling again and again from some discrete population. Thus, the KSL DPopulation class can serve as a starting point. Alternatively, the KSL EmpiricalRV class can be used. Let’s start with a simple example that has an original sample size of 10 elements. For example, assume through some sampling process we have selected 10 students (at random) and counted the number of books in their backpack. The following code illustrates placing the data in an array and computing some basic statistics related to the sample.
Example 9.1 (Bootstraping Example 1) This example defines a population of values within an array. Then, the example uses the DPopulation class to sample from the population. Statistics on the samples are captured and used to form a confidence interval.
// make a population for illustrating bootstrapping
val mainSample = doubleArrayOf(6.0, 7.0, 5.0, 1.0, 0.0, 4.0, 6.0, 0.0, 6.0, 1.0)
println("Sample of size 10 from original population")
println(mainSample.joinToString())
println()
// compute statistics on main sample
val mainSampleStats = Statistic(mainSample)
println("Main Sample")
println("average = ${mainSampleStats.average}")
println("90% CI = ${mainSampleStats.confidenceInterval(.90)}")
println()Running this code results in the following:
Sample of size 10 from original population
6.0, 7.0, 5.0, 1.0, 0.0, 4.0, 6.0, 0.0, 6.0, 1.0
Main Sample
average = 3.599999999999999
90% CI = [1.978733917471777, 5.221266082528222]In the notation that we have been using \(\bar{x} = \hat{\theta} = 3.5\bar{9}\). The sample size is small and it is very unlikely that the distribution of the number books in a student’s backpack would be normally distributed. Therefore, the reported confidence interval is certainly approximate. The KSL Statistic class reports its confidence interval assuming a Student-T distribution. We would like to use bootstrapping to produce a confidence interval. We can get started by treating our original sample as if it is the population and sampling from it. Here is some KSL code to illustrate this process.
// make the sample our pseudo-population
val samplePopulation = DPopulation(mainSample)
val bootStrapAverages = mutableListOf<Double>()
// illustrate 10 bootstrap samples
println("BootStrap Samples:")
for (i in 1..10){
val bootStrapSample = samplePopulation.sample(10)
val avg = bootStrapSample.average()
println("sample_$i = (${bootStrapSample.joinToString()}) with average = $avg")
bootStrapAverages.add(avg)
}
println()
val lcl = Statistic.percentile(bootStrapAverages.toDoubleArray(), 0.05)
val ucl = Statistic.percentile(bootStrapAverages.toDoubleArray(), 0.95)
val ci = Interval(lcl, ucl)
println("Percentile based 90% ci = $ci")In this code, we first create an instance of DPopulation using the array of observations of the book count data. Then, a list is created to hold the averages of each bootstrap sample. The loop creates 10 bootstrap samples and captures the average of each sample. Notice that the DPopulation is used to sample with replacement a sample of size 10. It is important that the sample size, 10, be the same as the size of the original sample because our confidence statements are about the original sample (with size 10). Given the bootstrap averages are captured in a list, bootStrapAverages, we can then use the percentile method to get the lower and upper limits for the confidence interval based on the bootstrap reference distribution.
BootStrap Samples:
sample_1 = (0.0, 1.0, 1.0, 7.0, 1.0, 1.0, 1.0, 0.0, 1.0, 1.0) with average = 1.4
sample_2 = (5.0, 1.0, 1.0, 6.0, 4.0, 7.0, 0.0, 1.0, 5.0, 6.0) with average = 3.6
sample_3 = (0.0, 5.0, 4.0, 6.0, 1.0, 4.0, 7.0, 0.0, 1.0, 6.0) with average = 3.4
sample_4 = (6.0, 5.0, 0.0, 1.0, 6.0, 6.0, 6.0, 1.0, 6.0, 1.0) with average = 3.8
sample_5 = (5.0, 1.0, 0.0, 0.0, 0.0, 1.0, 0.0, 6.0, 6.0, 6.0) with average = 2.5
sample_6 = (4.0, 7.0, 1.0, 0.0, 0.0, 0.0, 0.0, 7.0, 0.0, 1.0) with average = 2.0
sample_7 = (5.0, 6.0, 1.0, 6.0, 0.0, 6.0, 6.0, 1.0, 5.0, 7.0) with average = 4.3
sample_8 = (7.0, 6.0, 4.0, 1.0, 1.0, 1.0, 6.0, 1.0, 7.0, 6.0) with average = 4.0
sample_9 = (0.0, 6.0, 1.0, 6.0, 6.0, 5.0, 7.0, 4.0, 1.0, 1.0) with average = 3.7
sample_10 = (5.0, 6.0, 7.0, 0.0, 6.0, 6.0, 5.0, 0.0, 1.0, 0.0) with average = 3.6
Bootstrap sample averages
1.4, 3.6, 3.4, 3.8, 2.5, 2.0, 4.3, 4.0, 3.7, 3.6
Percentile based 90% ci = [1.4, 4.3]The results show 10 bootstrap samples. Notice that due to sampling with replacement, we can have values in the bootstrap samples that repeat and that it is clearly possible that some observations within the original sample, do not appear in the bootstrap samples. It is important to note that this bootstrap confidence interval is for our original estimate, \(\bar{x} = \hat{\theta} = 3.5\bar{9}\). The bootstrap sample averages, \((1.4, 3.6, 3.4, 3.8, 2.5, 2.0, 4.3, 4.0, 3.7, 3.6)\) represent the bootstrap estimate of the sampling distribution of \(\hat{\theta}^{*}_{b}\), \(F_{\hat{\theta}^{*}_{b}}(\cdot)\), which we are using as an approximation for the sampling distribution of \(\hat{\theta}\).
The idea of repeatedly sampling from a given population has been implemented into a set of classes within the KSL that will perform the bootstrapping process and compute a variety of quantities (including confidence intervals) based on the bootstrap samples. Figure 9.1 presents the BootstrapEstimateIfc interface, the main implementation of this interface (Bootstrap), and a data class, BootstrapEstimate, that is useful when building approaches that require bootstrapping.

Figure 9.1: KSL Bootstrap Classes
The Bootstrap class requires an array of doubles that represents the original data from which resampling will occur. While implementing the BootstrapEstimateIfc interface, the Bootstrap class also implements the RNStreamControlIfc, and RNStreamChangeIfc interfaces, which allow for the control of the underlying random numbers used within the sampling. It is useful to review the constructor of the Bootstrap class.
open class Bootstrap(
originalData: DoubleArray,
val estimator: BSEstimatorIfc = BSEstimatorIfc.Average(),
streamNumber: Int = 0,
val streamProvider: RNStreamProviderIfc = KSLRandom.DefaultRNStreamProvider,
name: String? = null
) : IdentityIfc by Identity(name), RNStreamControlIfc, BootstrapEstimateIfc, StreamNumberIfcAs noted in the constructor, the class requires an array holding the original data, an instance of the BSEstimatorIfc interface, the stream for the random sampling and an optional name. The BSEstimatorIfc interface is a functional interface with an estimate() function. Thus, this implementation assumes that the estimate can be computed from a uni-variate array of data and produces a single estimated quantity. The KSL also supports multiple estimated quantities from a uni-variate array of data.
As can be noted from the default parameter for the estimator, the BSEstimatorIfc interface provides some basic statistical estimators (average, variance, median, minimum, maximum). Of course, the user should be able to implement others as needed.
According to Figure 9.1, the Bootstrap class also will compute the following:
- the bootstrap replicates, \(\hat{\theta}^{*}_{b}\)
- the bootstrap differences, \(\hat{\theta}^{*}_{b} - \hat{\theta}\)
- across bootstrap statistics, statistics on the replicates
- statistics for each bootstrap sample
- boot strap bias estimate
- boot strap standard error estimate
- normal bootstrap confidence interval
- basic bootstrap confidence interval
- percentile bootstrap confidence interval
- BCa bootstrap confidence interval
- bootstrap-t confidence interval
Once constructing an instance of the Bootstrap class is complete, you can call the generateSamples() function. The following code shows the generateSamples() function. The function requires the number of bootstrap samples to generate, and optionally, you can have the bootstrap samples saved, and indicate if the bootstrap-t samples are required.
fun generateSamples(numBootstrapSamples: Int, saveBootstrapSamples: Boolean = false,
numBootstrapTSamples: Int = 0
) {
require(numBootstrapSamples > 1) { "The number of bootstrap samples must be greater than 1" }
if (numBootstrapTSamples > 0) {
require(numBootstrapTSamples > 1) { "The number of bootstrap-t samples must be greater than 1" }
}
this.numBootstrapSamples = numBootstrapSamples
myAcrossBSStat.reset()
myBSEstimates.clearData()
myStudentizedTValues.clearData()
for (s in myBSArrayList) {
s.clearData()
}
myBSArrayList.clear()
originalDataEstimate = estimator.estimate(myOriginalData)
for (i in 0 until numBootstrapSamples) {
val sample: DoubleArray = myOriginalPop.sample(myOriginalPop.size())
val x = estimator.estimate(sample)
myAcrossBSStat.collect(x)
myBSEstimates.save(x)
if (saveBootstrapSamples) {
val das = DoubleArraySaver()
das.save(sample)
myBSArrayList.add(das)
}
if (numBootstrapTSamples > 1) {
bootstrapTSampling(numBootstrapTSamples, x, sample)
}
innerBoot(x, sample)
}
}This code is rather straightforward, having a loop to implement the sampling. In essence, it is not much different conceptually than the previously code using the DPopulation class.
Example 9.2 (Bootstraping Example 2) To setup and run bootstrapping using the Bootstrap class, we have the following code:
// make a population for illustrating bootstrapping
val mainSample = doubleArrayOf(6.0, 7.0, 5.0, 1.0, 0.0, 4.0, 6.0, 0.0, 6.0, 1.0)
println("Sample of size 10 from original population")
println(mainSample.joinToString())
println()
// compute statistics on main sample
val mainSampleStats = Statistic(mainSample)
println("Main Sample")
println("average = ${mainSampleStats.average}")
println("90% CI = ${mainSampleStats.confidenceInterval(.90)}")
println()
// now to the bootstrapping
val bs = Bootstrap(mainSample, estimator = BSEstimatorIfc.Average(), streamNumber = 3)
bs.generateSamples(400, numBootstrapTSamples = 399)
println(bs)Running this code results in the following:
Sample of size 10 from original population
6.0, 7.0, 5.0, 1.0, 0.0, 4.0, 6.0, 0.0, 6.0, 1.0
Main Sample
average = 3.5999999999999996
90% CI = [1.978733917471777, 5.221266082528222]
------------------------------------------------------
Bootstrap statistical results:
label = ID_4
------------------------------------------------------
statistic name = ID_4
number of bootstrap samples = 400
size of original sample = 10
original estimate = 3.5999999999999996
bias estimate = -0.05175000000000063
across bootstrap average = 3.548249999999999
bootstrap std. err. estimate = 0.04007502167379812
default c.i. level = 0.95
norm c.i. = [3.5214544007763693, 3.67854559922363]
basic c.i. = [2.002500000000003, 5.2974999999999985]
percentile c.i. = [1.902500000000001, 5.197499999999996]
BCa c.i. = [1.9000000000000001, 5.062949171806798]
bootstrap-t c.i. = [1.9000000000000001, 5.062949171806798]
------------------------------------------------------In these results, it just happens that the BCa and bootstrap-t result in the same intervals. The main question that comes up when bootstrapping is what value should be used for the number of bootstrap samples, \(B\). (Efron and Tibshirani 1994) provide some guidance indicating a range at least starting in the hundreds. There has been some work that suggests the the quality of the process is a function of \(n\), the size of the original sample. The work suggests that larger \(n\) requires larger \(B\). The relationship \(B \approx 40n\) has been suggested.
As previously mentioned, the KSL also supports the estimation of multiple quantities from the sample. This functionality is used extensively within the distribution modeling functionality of the KSL to provide confidence intervals on the parameters of distributions. Figure 9.2 presents the BootstrapSampler class, which will compute multiple estimators on a sample using the MVBSEstimatorIfc interface.
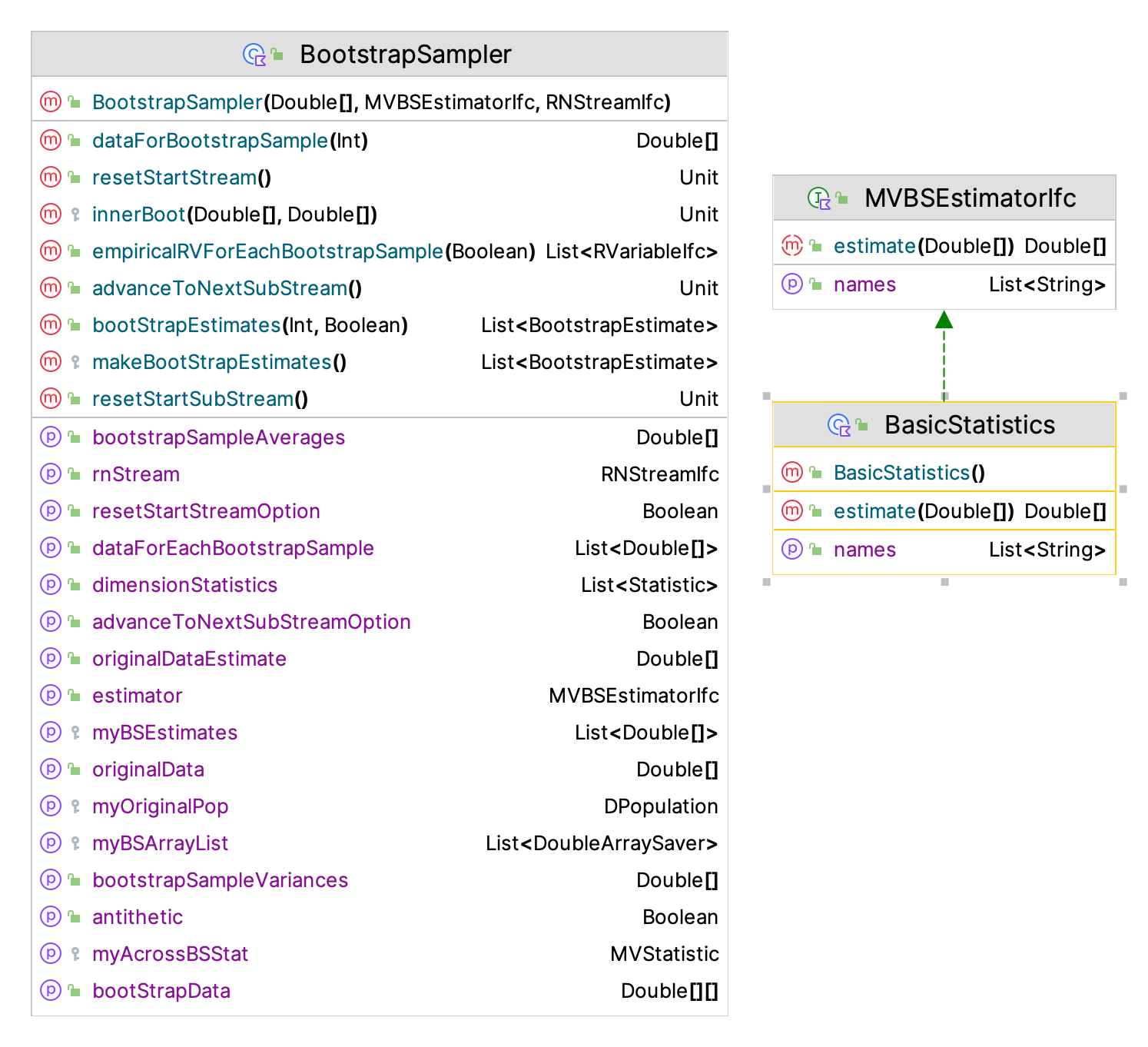
Figure 9.2: KSL BootstrapSampler Classes
As shown in the following code, the MVBSEstimatorIfc interface defines a function that takes in a sample and returns many estimated quantities.
/**
* Given some data, produce multiple estimated statistics
* from the data and store the estimated quantities in
* the returned array. It is up to the user to interpret
* the array values appropriately.
*/
interface MVBSEstimatorIfc {
/**
* The name to associate with each dimension of the
* array that is returned by estimate(). The names
* should be unique. The order of the list of names should
* match the order of elements in the returned array.
*/
val names: List<String>
fun estimate(data: DoubleArray): DoubleArray
}Example 9.3 (Illustrating the BootstrapSampler Class) The following code illustrates the use of the BootstrapSampler class. This provides bootstrap estimates for basic statistics.
This code samples from an exponential distribution to get the initial sample and then uses the BootstrapSampler class to provide bootstrap estimates for the basic statistics. The BasicStatistics class is just a simple implementation of the MVBSEstimatorIfc interface that computes the average, variance, minimum, maximum, skewness, kurtosis, lag-1 correlation, and lag-1 covariance.
@Suppress("unused")
class BasicStatistics(aName: String? = null) : MVBSEstimatorIfc, IdentityIfc by Identity(aName){
private val stat = Statistic()
override val names: List<String> = listOf(
"average", "variance", "min", "max", "skewness", "kurtosis",
"lag1Correlation", "lag1Covariance")
override fun estimate(data: DoubleArray): DoubleArray {
stat.reset()
stat.collect(data)
val array = DoubleArray(8)
array[0] = stat.average
array[1] = stat.variance
array[2] = stat.min
array[3] = stat.max
array[4] = stat.skewness
array[5] = stat.kurtosis
array[6] = stat.lag1Correlation
array[7] = stat.lag1Covariance
return array
}
}This same approach could be used to add additional statistics. The output from the sampling can be quite extensive and thus is not provided here. For a final discussion of bootstrapping, we discuss the KSL capabilities for bootstrapping cases and illustrate its application to bootstrapping a simple regression model.
The previous KSL bootstrapping functionality focused on uni-variate data. The same concepts can also be applied to multi-variate data. Since the data structures to hold multi-variate data can be complex, we focus on representing the population of items via identifiers. That is, we assume that each item in the population can be assigned a unique label and that the sampling and resampling process takes place on the set of identifiers. The sampled identifiers then can be used to index into some complex data structure to select the sampled items. Then from each item, a set of values are observed. Thus, each sampled item, \(i\), results in a set of observations \(\vec{x_i}=x_1, x_2, \cdots, x_m\), where \(m\) is the number of attributes observed about each item. In some bootstrapping literature, the set of sampled items is called the cases, with each item called a case. Thus, in this situation, the bootstrapping process is sometimes called case based bootstrapping.
Within a programming context, we can represent each item with an object, which has some attributes. The attributes represent the data observed about the object. Placing the objects into a collection, permits sampling from the collection. For example, the cases could be the rows in a regression data set. The data could be stored in arrays, in data frames, database tables, etc. As long as each item the population can be uniquely labeled, we can sample the labels, and then select the items based on their identifiers.

Figure 9.3: KSL CaseBootstrapSampler Classes
Figure 9.3 presents the CaseBootstrapSampler class, which will compute multiple estimators using case based sample via the CaseBootEstimatorIfc interface. This sampler has similar functionality as the BootstrapSampler class. As in the BootstrapSampler situation, we assume that the estimation process may result in one or more estimated quantities; however, in this situation, the estimation process requires a set of items from which the quantities will be computed.
It should be instructive to review the associated interfaces in Figure 9.3. The CaseBootstrapSampler class requires an instance of the CaseBootEstimatorIfc interface. The CaseBootEstimatorIfc interface does not define the data structure associated with the sampling process. Instead, it defines a list of identifiers that represent the finite sample from which bootstrap sampling occurs.
interface CaseBootEstimatorIfc {
/**
* The name to associate with each dimension of the
* array that is returned by estimate(). The names
* should be unique. The order of the list of names should
* match the order of elements in the returned array. This
* list is used to label the elements that are estimated.
*/
val names: List<String>
/**
* The estimates from the estimator based on the original (not resampled) data.
*/
val originalEstimates: DoubleArray
/**
* The set of case identifiers. This set must hold unique
* integers that serve as the sampling population. Elements (cases)
* are sampled with replacement from this set to specify
* the data that will be used in the estimation process.
*/
val caseIdentifiers: List<Int>
/**
* The [caseIndices] array contains the case identifiers that
* should be used to select the data on which the estimation
* process should be executed. The function produces an
* array of estimates during the estimation process, which
* are associated with the labels in the names list. The
* case indices array may have repeated case identifiers
* due to sampling with replacement.
*/
fun estimate(caseIndices: IntArray): DoubleArray
}As we can see from the previous Kotlin code, the names and originalEstimates properties have a similar functionality as in the BootstrapSampler class. The names are the labels for the things estimated from the sample.
The property, caseIdentifiers is a list holding the identifiers for the cases. For example, if the cases are rows in a regression dataset, then the list might hold the values \((0,1,2,\cdots,n-1)\), where \(n\) is the number of rows. That is, the list holds the indices of the rows. The sampling process will sample from the identifier population and use the identifiers to access the actual items. This approach necessitates a different estimate() function. Here, the estimation process, requires an array of integers that represent the identifiers of the cases selected to be included in the estimation process. Note that because the sampling is with replacement, the same item can be selected multiple times (or not at all) during the bootstrap sampling. Conceptually, this is no different from what we have previously illustrated, but now our population is simply a set of identifiers.
The class MatrixBootEstimator is simply an implementation of the CaseBootEstimatorIfc interface designed to work with a rectangular array (i.e. a matrix) of data, where the rows are the cases. The interface MatrixEstimatorIfc is a convenience interface for directly computing the statistical quantities from a supplied matrix. The selection process for MatrixBootEstimator is simply to select the rows as shown in the following code.
override fun estimate(caseIndices: IntArray): DoubleArray {
// select the rows of the matrix from the supplied indices
val m = Array(matrix.size) { matrix[caseIndices[it]] }
return matrixEstimator.estimate(m)
}The CaseBootstrapSampler class samples the indices (mySample) in the following code, which is then supplied to the estimate(caseIndices: IntArray) function.
fun sampleCases(): IntArray {
for (i in myOriginalPopulation.indices) {
val index = rnStream.randInt(0, myOriginalPopulation.size - 1)
mySample[i] = myOriginalPopulation[index]
}
return mySample
}Finally, the object OLSBootEstimator, in Figure 9.3, is an object that implements the MatrixEstimatorIfc interface an computes the regression coefficients by assuming that the first column of the matrix is the regressor, \(Y\), and the remaining columns represent the predictor matrix \(X\). Because of the fact that we use the ordinary least squares estimation routines from the Hipparchus library, the \(X\) matrix does not need to include the column for estimating the intercept term.
Putting all of these concepts together, we can illustrate the bootstrapping of a regression estimation process. As shown in the following code, we generate some regression data. For simplicity, we assume normally distributed predictors and error.
Example 9.4 (Illustrating Case Based Bootstrapping) This example illustrates case based bootstrapping for a linear regression model.
// first make some data for the example
val n1 = NormalRV(10.0, 3.0)
val n2 = NormalRV(5.0, 1.5)
val e = NormalRV()
// make a simple linear model with some error
val data = Array<DoubleArray>(100) {
val x1 = n1.value
val x2 = n2.value
val y = 10.0 + 2.0*x1 + 5.0*x2 + e.value
doubleArrayOf(y, x1, x2)
}
//data.write()
// apply bootstrapping to get bootstrap confidence intervals on regression parameters
val cbs = CaseBootstrapSampler(MatrixBootEstimator(data, OLSBootEstimator))
val estimates = cbs.bootStrapEstimates(399)
// print out the bootstrap estimates
for(be in estimates){
println(be)
}The results of the bootstrapping process are as follows. As we can see, the confidence intervals for the known regression coefficients \((\beta_0=10.0, \beta_1=2.0, \beta_2=5.0\)) do a reasonable job of covering the known quantities.
------------------------------------------------------
Bootstrap statistical results:
------------------------------------------------------
statistic name = b0
number of bootstrap samples = 399
size of original sample = 100
original estimate = 10.997223980092517
bias estimate = 0.09157195462246293
across bootstrap average = 11.08879593471498
bootstrap std. err. estimate = 0.04090939870934704
default c.i. level = 0.95
norm c.i. = [10.917043031928365, 11.07740492825667]
basic c.i. = [9.052998742918017, 12.427568666255603]
percentile c.i. = [9.566879293929432, 12.941449217267017]
------------------------------------------------------
Bootstrap statistical results:
------------------------------------------------------
statistic name = b1
number of bootstrap samples = 399
size of original sample = 100
original estimate = 1.9494963162125691
bias estimate = -0.0037025407662301113
across bootstrap average = 1.945793775446339
bootstrap std. err. estimate = 0.002936548908845975
default c.i. level = 0.95
norm c.i. = [1.9437407861077505, 1.9552518463173878]
basic c.i. = [1.84302999325699, 2.0787441726888636]
percentile c.i. = [1.8202484597362747, 2.0559626391681483]
------------------------------------------------------
Bootstrap statistical results:
------------------------------------------------------
statistic name = b2
number of bootstrap samples = 399
size of original sample = 100
original estimate = 4.9390811206920375
bias estimate = -0.010600231082452005
across bootstrap average = 4.9284808896095855
bootstrap std. err. estimate = 0.004055345194183637
default c.i. level = 0.95
norm c.i. = [4.931132790160152, 4.947029451223923]
basic c.i. = [4.794185241695615, 5.111679266251416]
percentile c.i. = [4.766482975132659, 5.08397699968846]For more of the theory and methods of bootstrapping within the context of regression, we refer the interested reader to the text, (Fox and Weisberg 2018). Since the purpose of this section was to illustrate how the KSL facilitates bootstrapping, the interested reader may want to explore more of the theory. From that standpoint, the books by (Efron and Tibshirani 1994) and (Davison AC 1997) are good starting points. See also the paper (Efron and Tibshirani 1986).