10.4 Representing the Simulation Oracle

The simulation oracle is a term used to represent the concept of the simulation model as a “black-box” that accepts inputs and returns outputs as illustrated in Figure 10.8. To be able to define general problems and have them solved by general algorithms, a protocol needs to be established to represent the inputs, the model, and the outputs for generation, use, and consumption by optimization solvers. The purpose of the ksl.simopt.evaluator package is to provide classes and interfaces that establish this interaction protocol.

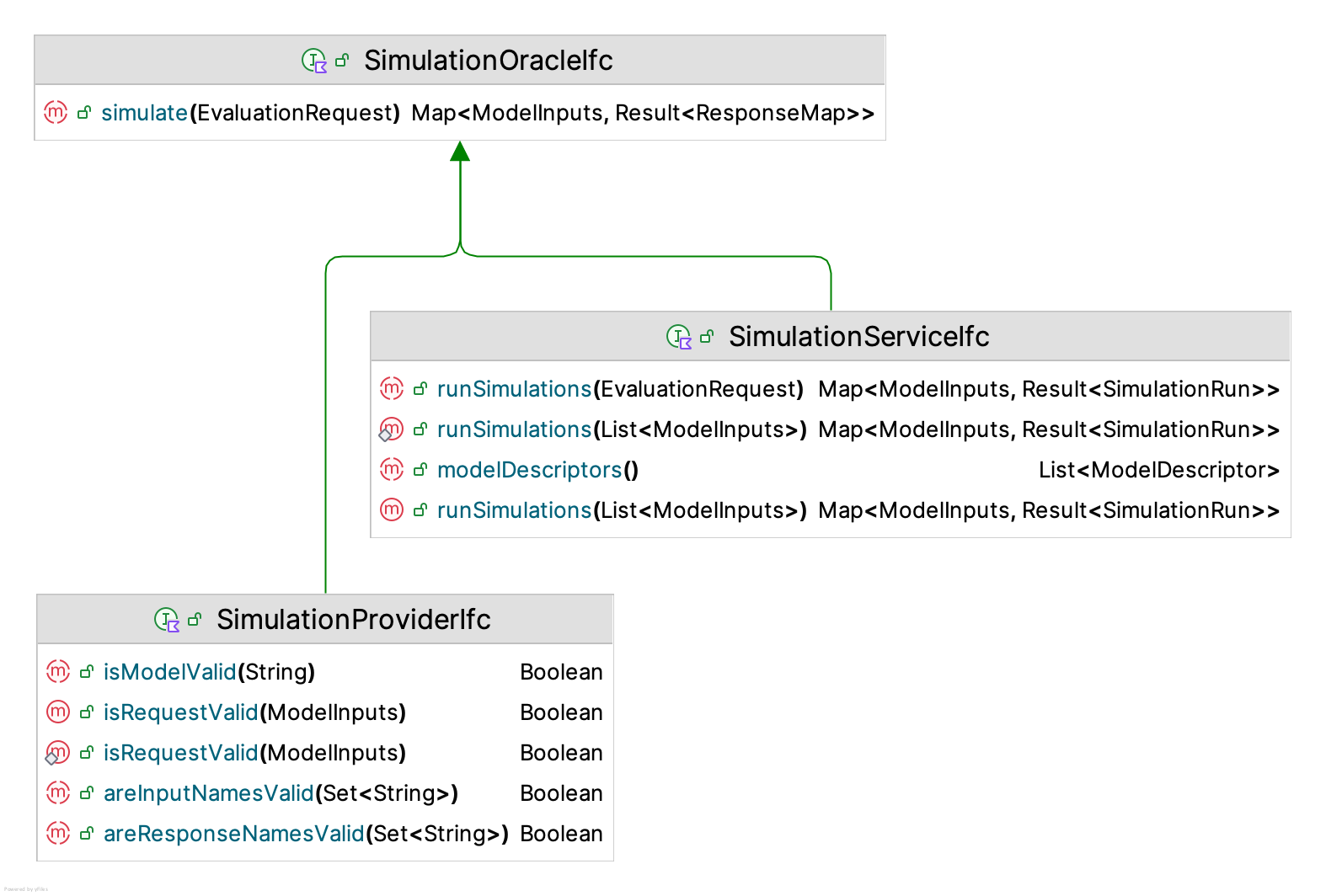
Figure 10.14: Simulation Oracle Interfaces

Figure 10.14 presents three major interfaces which support the general execution of KSL simulation models. The SimulationOracleIfc interface provides behavior that receives evaluation requests (inputs) and translates those requests to simulation results. An implementer of the SimulationProviderIfc interface is a simulation oracle that has additional functionality to validate evaluation requests. A simulation provider is associated with a single simulation model. The SimulationServiceIfc interface also implements the SimulationOracleIfc interface and has the capability to execute simulation requests for multiple models.

10.4.1 Requesting Simulation Evaluations

This discussion will focus on the simulation oracle and how it relates to the EvaluatorIfc interface shown in Figure 10.15.

Figure 10.15: Simulation Evaluator Interfaces

As we will see in the section concerning solvers, solvers use implementations of the EvaluatorIfc interface to request simulation evaluations. As can be seen in Figure 10.15, the constructor for the Evaluator class requires an instance of the ProblemDefinition class and an instance of an implementation of the SimulationOracleIfc interface. In essence, implementations of the EvaluatorIfc interface translate simulation results into in solutions that solvers can use. The following will overview this process starting with what it means to make a request for a simulation evaluation.

The process for requesting a simulation execution starts with an instance of the EvaluationRequest class. As shown in Figure 10.16, an evaluation request is a data class which holds model inputs and options for the simulation execution process.

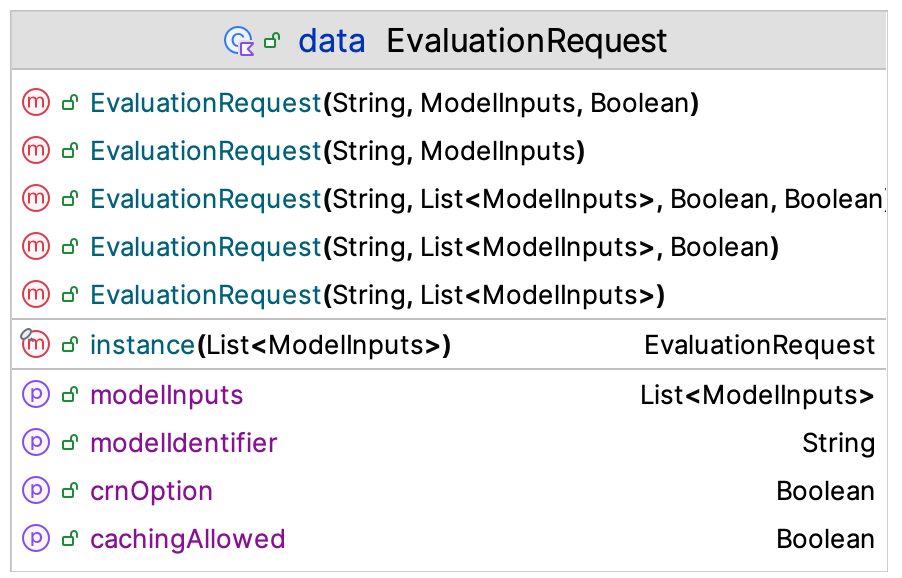
Figure 10.16: Evaluation Requests

An evaluation request represents many possible evaluations in the form of a list of model inputs. The evaluation request specifies the model via the model identifier, whether the evaluations should be run with common random numbers, and whether cached results can be used to satisfy the request. The option to run the evaluations with common random numbers is only valid if there are two or more requested evaluations (i.e. the list of model inputs has two or more elements). In addition, using cached results is not allowed if the request uses common random numbers. Thus, an evaluation request represents a set of simulation executions that will be handled by the simulation oracle. The evaluation requests are translated into a map of model inputs with the results within a map of responses. Let’s take a closer examination of these two concepts.

10.4.2 Representing Model Inputs

As noted in Figure 10.16, an evaluation request consists of a list of model inputs. A model input is a specification for the inputs that will be used for the simulation run and the outputs that are requested. Figure 10.17 shows the ModelInputs class.

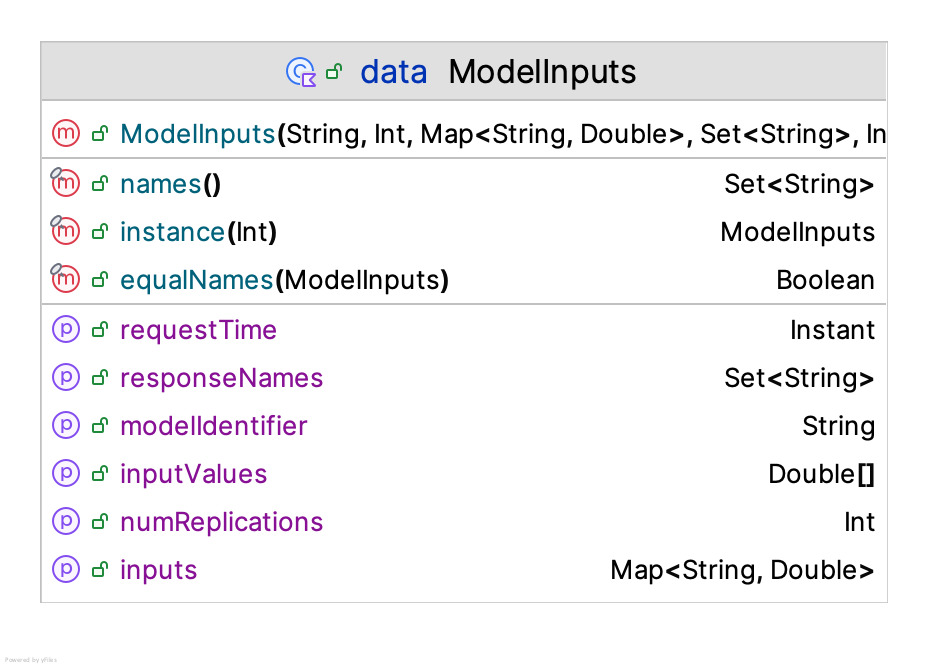
Figure 10.17: Model Inputs

The ModelInputs class is also a Kotlin data class. As can be noted in the data class’s constructor, model inputs require the model identifier, the number of replications for the simulation run, the inputs (specified as name, value pairs in a map), and the names of the responses required from the simulation run. If the inputs map is empty, the current settings of the simulation model are used for the simulation execution. If the set of response names is empty, then all responses from the simulation are returned.

data class ModelInputs(
    val modelIdentifier: String,
    val numReplications: Int,
    val inputs: Map<String, Double> = emptyMap(),
    val responseNames: Set<String> = emptySet(),
    val requestTime: Instant = Clock.System.now()
)

Model inputs have a very special representation for determining their equality. Two instances of the ModelInputs class are considered equal if:

the modelIdentifier properties are equal, and
the responseNames properties are equal (contain all the same response names), and
the inputs properties are equal (contain the same (key, value) pairs)

It is important to note that two instances will be considered equal even if their number of requested replications are different. This definition of equality facilitates the caching of results by model inputs.

So far, we have discussed the inputs to the simulate() function of the SimulationOracleIfc interface. Each model input in the evaluation request is paired with the requested responses in the form of a map. The SimulationOracleIfc interface prescribes that the responses are wrapped within a Kotlin Result instance. A Kotlin Result indicates whether an outcome from a process was a success or a failure. Since simulation evaluations may be executed remotely via simulation services, there are many opportunities for failure to occur (e.g. network failure, service denial, etc.). A more likely scenario is that some execution error occurred during the simulation run. Thus, the user of the simulation oracle can react according to the success or failure of the request.

interface SimulationOracleIfc {

    fun simulate(evaluationRequest: EvaluationRequest): Map<ModelInputs, Result<ResponseMap>>

}

10.4.3 Representing Model Outputs

Now we can discuss the ResponseMap class. The ResponseMap class, illustrated in Figure 10.18, is also a Kotlin data class. The use of data classes for the mappings between inputs and outputs is an intentional part of the package design. The data classes are serializable, which facilitates their distribution via network calls.

Figure 10.18: The ResponseMap Class

The ResponseMap class is a map. In fact, it implements the Map<String, EstimatedResponse> interface. The string key for the map is the name of the response (as per the model and the EvaluationRequest) and the paired value is an instance of the EstimatedResponse class. The EstimatedResponse class, illustrated in Figure 10.19, holds basic summary statistics across the replications associated with the simulation run. The ResponseMap class has functionality that facilitates the reporting of statistics for its contained EstimatedResponse instances. In addition, the ResponseMap class facilitates the merging of the responses that it contains. This is important for the case of solvers that may revisit decision points with additional requests for replications. If caching is available, then the results from previous samples are merged with new samples so that the cached replications can partially fill the request.

Figure 10.19: The EstimatedResponse Class

Suppose we have two estimates for the same response, with summary statistics (\(\bar{x}_1\), \(s^2_1\), \(n_1\)) and (\(\bar{x}_2\), \(s^2_2\), \(n_2\)). Merging of the two response estimates, creates a single estimated response (\(\bar{x}\), \(s^2\), \(n\)). We assume that the two estimates are from independent samples. The values for \(n\) and \(\bar{x}\) are as follows:

\[ n = n_1 + n_2\\ \bar{x} = \frac{n_1\bar{x}_1+n_2\bar{x}_2}{n} \] Thus, \(\bar{x}\) is the weight-average of the estimates. The computation of \(s^2\) follows the idea of a pooled variance. For the case where \(n_1 >2\) and \(n_2 > 2\), we can compute the weighted average:

\[ s^2 = \frac{(n_1-1)s^2_1+(n_2-1)s^2_2}{n-2} \] The case where \(n_1 = 1\) and \(n_2 = 1\) can be handled easily by noting that this is the same as two independent observations. The cases where \(n_1 = 1\) and \(n_2 = 2\) or \(n_1 = 2\) and \(n_2 = 1\) can be handled by noting that the situation with \(n_i=1\) is just adding an additional observation to a statistical summary. The assumption that the estimates are independent is important when computing the variances. This is one of the main reasons that necessitates not using cached results when common random numbers is used.

Within the context of an optimization problem, the algorithms require solutions. This brings up the final topic of this section. The translation of responses to solutions. As noted at the beginning of this section, solvers require the implementation of the EvaluatorIfc interface. As we can see from the definition of the interface, the interface provides a translation from evaluation requests to solutions. Every request to the simulation oracle for a set of inputs is translated to a map that contains the model inputs that resulted in the returned solution.

interface EvaluatorIfc {

    /**
     *  A possible cache to hold evaluated solutions
     */
    val cache: SolutionCacheIfc?

    /**
     *  Processes the supplied requests for solutions. The solutions may come from an associated
     *  solution cache (if present or allowed) or via evaluations by the simulation oracle.
     *  The CRN option is applied to the set of requests and does not permit
     *  cached solutions, even if caching is permitted.
     *
     *  @param evaluationRequest a request for evaluation
     *  @return a map containing the model inputs and resulting solutions as pairs
     */
    fun evaluate(evaluationRequest: EvaluationRequest): Map<ModelInputs, Solution>

}

Figure 10.20 presents the Solution class. Again, the Solution class is a Kotlin data class. It holds the inputs that caused the solution, the objective function, and a list of the estimated responses for the response constraints.

Figure 10.20: The Solution Class

As we can see from the constructor, the inputMap property holds the inputs associated with the solution. The estimatedObjFnc property represents the estimated objective function value as an EstimatedResponse instance. The responseEstimates property hold the list of the response associated with the response constraints. The evaluationNumber is an integer that marks the current number of evaluations performed by the evaluator that produced the solution. In essence, calls for evaluation produce a sequence of solutions. The isValid property is used to indicate whether the solution is valid. A solution will be invalid if there was some problem or exception that occurred during the evaluation process. Invalid solutions will also be constructed as bad solutions. Essentially, a bad solution is a solution that is infeasible and has the worse possible objective function value with respect to the problem instance.

data class Solution(
    val inputMap: InputMap,
    val estimatedObjFnc: EstimatedResponse,
    val responseEstimates: List<EstimatedResponse>,
    val evaluationNumber: Int,
    val isValid: Boolean = true
) : Comparable<Solution>, FeasibilityIfc by inputMap, EstimatedResponseIfc by estimatedObjFnc

As can be noted by the constructor, solutions can be compared and their feasibility checked. Feasibility is established with respect to the problem instance. There are four types of feasibility modeled.

Input range feasibility - If the input values are within the ranges defined for the input variable, then the solution is considered input range feasible.
Linear constraint feasibility - If the input values satisfy all linear constraints, then the solution is considered feasible with respect to the linear constraints.
Functional constraint feasibility - If the input values satisfy all functional constraints, then the solution is consider feasible with respect to the functional constraints.
Input feasible - If the input values are input range feasible, linear constraint feasible, and functional constraint feasible, then the solution is considered input feasible.

Notice that feasibility ignores the issue of feasibility with respect to the response constraints. Essentially, input feasibility is checking the inputs. It does not check the outputs (response). A solution implements the EstimatedResponseIfc interface based on the value of the estimated objective function response.

To summarize, the procedures defined in the ksl.simopt.evaluator package permit requests for simulation evaluations. The inputs to the simulation model are contained within the request. The simulation model is executed at the specified inputs and the requested results returned. For simulation optimization algorithms, the input-output mapping is encapsulated within instances of the Solution class. The Solution class contains information on the following:

The inputs used to execute the simulation.
The value of the objective function estimated via simulation, the penalized objective function value, and the constraint violations.
The estimated responses involved in any response constraints.
The ability to assess the feasibility of the solution with respect to the inputs and deterministic constraints.

The information from solutions is designed to be consumed by simulation optimization algorithms, which is the topic of the next section.