3.10 Exercises
Exercise 3.1 Compute the required sample size necessary to ensure a 95% confidence interval with a half-width of no larger than 30 minutes for the total time to produce a part. Given the half-width of the system time after 10 runs is 47.25, compute the sample size using the half-width ratio method. Round the answer to the next highest integer.
Exercise 3.2 Compute the required sample size necessary to ensure a 95% confidence interval with a half-width of no larger than 30 minutes for the total time to produce a part. Given the half-width of the system time after 10 runs is 47.25. Find the approximate number of replications needed in order to have a 99% confidence interval that is within plus or minus 2 minutes of the true mean system time using the half-width ratio method.
Exercise 3.3 Assume that the following results represent the summary statistics for a pilot run of 10 replications from a simulation for the system time in minutes. \(\overline{x} = 78.2658 \; \pm 9.39\) with confidence 95%. Find the approximate number of additional replications in order to have a 99% confidence interval that is within plus or minus 2 minutes of the true mean system time.
Exercise 3.4 Suppose \(n=10\) observations were collected on the time spent in a manufacturing system for a part. The analysis determined a 95% confidence interval for the mean system time of \([18.595, 32.421]\).
- Find the approximate number of samples needed to have a 95% confidence interval that is within plus or minus 2 minutes of the true mean system time.
- Find the approximate number of samples needed to have a 99% confidence interval that is within plus or minus 1 minute of the true mean system time.
Exercise 3.5 Suppose a pilot run of a simulation model estimated that the average waiting time for a customer during the day was 11.485 minutes based on an initial sample size of 15 replications with a 95% confidence interval half-width of 1.04. Using the half-width ratio sample size determination techniques, recommend a sample size to be 95% confident that you are within \(\pm\) 0.10 of the true mean waiting time in the queue. The half-width ratio method requires a sample size of what amount?
Exercise 3.6 Assume that the following table represents the summary statistics for a pilot run of 10 replications from a simulation.
| Simulation Statistics | NPV | P(NPV \(<\) 0) |
|---|---|---|
| Sample Average | 83.54 | 0.4 |
| Standard Deviation | 39.6 | 0.15 |
| Count | 10 | 10 |
Find the approximate number of additional replications to execute in order to have a 99% confidence interval that is within plus or minus 20 dollars of the true mean net present value using the normal approximation method.
Find the number of replications necessary to be 99% confident that you have an interval within plus or minus 2% of the true probability of negative present value.
Exercise 3.7 The service times for a automated storage and retrieval system has a shifted exponential distribution. It is known that it takes a minimum of 15 seconds for any retrieval. The rate parameter of the exponential distribution is \(\lambda = 45\) retrievals per second. Setup a model that will generate 20 observations of the retrieval times. Report the minimum, maximum, sample average, and 95% confidence interval half-width of the observations. Use stream 1 for your sampling.
Exercise 3.8 The time to failure for a computer printer fan has a Weibull distribution with shape parameter \(\alpha = 2\) and scale parameter \(\beta = 3\). Setup a model that will generate 50 observations of the failure times. Report the minimum, maximum, sample average, and 95% confidence interval half-width of the observations. Use stream 1 for your sampling.
Exercise 3.9 The time to failure for a computer printer fan has a Weibull distribution with shape parameter \(\alpha = 2\) and scale parameter \(\beta = 3\). Testing has indicated that the distribution is limited to the range from 1.5 to 4.5. Set up a model to generate 100 observations from this truncated distribution. Report the minimum, maximum, sample average, and 95% confidence interval half-width of the observations. Use stream 1 for your sampling.
Exercise 3.10 The interest rate for a capital project is unknown. An accountant has estimated that the minimum interest rate will between 2% and 5% within the next year. The accountant believes that any interest rate in this range is equally likely. You are tasked with generating interest rates for a cash flow analysis of the project. Set up a model to generate 100 observations of the interest rate values for the capital project analysis. Report the minimum, maximum, sample average, and 95% confidence interval half-width of the observations. Use stream 1 for your sampling.
Exercise 3.11 Develop a model to generate 30 observations from the following probability density function:
\[ f(x) = \begin{cases} \dfrac{3x^2}{2} & -1 \leq x \leq 1\\ 0 & \text{otherwise} \\ \end{cases} \] Report the minimum, maximum, sample average, and 95% confidence interval half-width of the observations. Use stream 1 for your sampling.
Exercise 3.12 Suppose that the service time for a patient consists of two distributions. There is a 25% chance that the service time is uniformly distributed with minimum of 20 minutes and a maximum of 25 minutes, and a 75% chance that the time is distributed according to a Weibull distribution with shape of 2 and a scale of 4.5. Use stream 1 for your sampling.
Setup a model to generate 100 observations of the service time. Compute the theoretical expected value of the distribution. Estimate the expected value of the distribution and compute a 95% confidence interval on the expected value. Did your confidence interval contain the theoretical expected value of the distribution?
Exercise 3.13 Suppose that \(X\) is a random variable with a \(N(\mu = 2, \sigma = 1.5)\) normal distribution. Generate 100 observations of \(X\) using a simulation model. Use stream 1 for your sampling.
Estimate the mean from your observations. Report a 95% confidence interval for your point estimate.
Estimate the variance from your observations. Report a 95% confidence interval for your point estimate.
Estimate the \(P(X>3)\) from your observations. Report a 95% confidence interval for your point estimate.
Exercise 3.14 Samples of 20 parts from a metal grinding process are selected every hour. Typically 2% of the parts need rework. Let \(X\) denote the number of parts in the sample of 20 that require rework. A process problem is suspected if \(X\) exceeds its mean by more than 1 standard deviation. Simulate 1000 hours of the process, i.e. 1000 samples of size 20, and estimate the chance that \(X\) exceeds its expected value by more than 1 standard deviation. Use stream 1 for your sampling.
Exercise 3.15 Consider the following discrete distribution of the random variable \(X\) whose probability mass function is \(p(x)\). Setup a model to generate 30 observations of the random variable \(X\). Use stream 1 for your sampling. Report the minimum, maximum, sample average, and 95% confidence interval half-width of the observations.
| \(x\) | 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|
| \(p(x)\) | 0.3 | 0.2 | 0.2 | 0.1 | 0.2 |
Exercise 3.16 The demand for parts at a repair bench per day can be described by the following discrete probability mass function. Setup a model to generate 30 observations of the demand. Use stream 1 for your sampling. Report the minimum, maximum, sample average, and 95% confidence interval half-width of the observations.
| Demand | 0 | 1 | 2 |
|---|---|---|---|
| Probability | 0.3 | 0.2 | 0.5 |
Exercise 3.17 Use the Monte Carlo method estimate the following integral with 95% confidence to within \(\pm 0.01\). Use stream 1 for your sampling.
\[\int\limits_{1}^{4} \left( \sqrt{x} + \frac{1}{2\sqrt{x}}\right) \mathrm{d}x\]
Exercise 3.18 Use the Monte Carlo method estimate the following integral with 99% confidence to within \(\pm 0.01\). Use stream 1 for your sampling.
\[\int\limits_{0}^{\pi} \left( \sin (x) - 8x^{2}\right) \mathrm{d}x\]
Exercise 3.19 Use the Monte Carlo method estimate the following integral with 99% confidence to within \(\pm 0.01\). Use stream 1 for your sampling.
\[\theta = \int\limits_{0}^{1} \int\limits_{0}^{1} \left( 4x^{2}y + y^{2}\right) \mathrm{d}x \mathrm{d}y\]
Exercise 3.20 A firm is trying to decide whether or not it should purchase a new scale to check a package filling line in the plant. The scale would allow for better control over the filling operation and result in less overfilling. It is known for certain that the scale costs $800 initially. The annual cost has been estimated to be normally distributed with a mean of $100 and a standard deviation of $10 (stream 1). The extra savings associated with better control of the filling process has been estimated to be normally distributed with a mean of $300 and a standard deviation of $50 (stream 2). The salvage value has been estimated to be uniformly distributed between $90 and $100 (stream 3). The useful life of the scale varies according to the amount of usage of the scale. The manufacturing has estimated that the useful life can vary between 4 to 7 years with the chances given in the following table (stream 4).
| years | 4 | 5 | 6 | 7 |
|---|---|---|---|---|
| f(years) | 0.3 | 0.4 | 0.1 | 0.2 |
| F(years) | 0.3 | 0.7 | 0.8 | 1.0 |
The interest rate has been varying recently and the firm is unsure of the rate for performing the analysis. To be safe, they have decided that the interest rate should be modeled as a beta random variable over the range from 6 to 9 percent with alpha = 5.0 and beta = 1.5 (stream 5). Given all the uncertain elements in the situation, they have decided to perform a simulation analysis in order to assess the expected present value of the decision and the chance that the decision has a negative return.
We desire to be 95% confident that our estimate of the true expected present value is within \(\pm\) 10 dollars. Develop a model for this situation.
Exercise 3.21 A firm is trying to decide whether or not to invest in two proposals A and B that have the net cash flows shown in the following table, where \(N(\mu, \sigma)\) represents that the cash flow value comes from a normal distribution with the provided mean and standard deviation.
| End of Year | 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|
| A | \(N(-150, 10)\) | \(N(475, 10)\) | \(N(275, 10)\) | \(N(275, 20)\) | \(N(250, 40)\) |
| B | \(N(-100, 5)\) | \(N(350, 10)\) | \(N(350, 10)\) | \(N(275, 20)\) | \(N(275, 30)\) |
The interest rate has been varying recently and the firm is unsure of the rate for performing the analysis. To be safe, they have decided that the interest rate should be modeled as a beta random variable over the range from 2 to 7 percent with \(\alpha_1 = 4.0\) and \(\alpha_2 = 1.2\). Given all the uncertain elements in the situation, they have decided to perform a simulation analysis in order to assess the situation. Use the KSL to answer the following questions:
Compare the expected present worth of the two alternatives. Estimate the probability that alternative A has a higher present worth than alternative B.
Determine the number of samples needed to be 95% confidence that you have estimated the \(P[PW(A) > PW(B)]\) to within \(\pm\) 0.10.
Use stream 1 for the cash flows and stream 2 for the interest rate.
Exercise 3.22 A U-shaped component is to be formed from the three parts A, B, and C. The picture is shown in the figure below. The length of A is lognormally distributed with a mean of 20 millimeters and a standard deviation of 0.2 millimeter (stream 1). The thickness of parts B (stream 2) and C (stream 3) is uniformly distributed with a minimum of 4.98 millimeters and a maximum of 5.02 millimeters. Assume all dimensions are independent.
Develop a model to estimate the probability that the gap \(D\) is less than 10.1 millimeters with 95% confidence to within plus or minus 0.01.
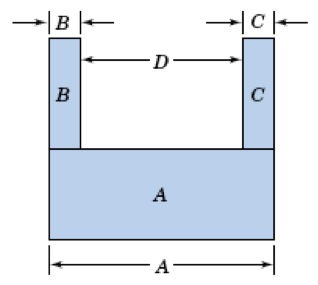
Figure 3.8: U-Shaped Component
Exercise 3.23 Shipments can be transported by rail or trucks between New York and Los Angeles. Both modes of transport go through the city of St. Louis. The mean travel time and standard deviations between the major cities for each mode of transportation are shown in the following figure.
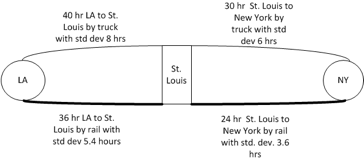
Figure 3.9: Truck Paths
Assume that the travel times (in either direction) are lognormally distributed as shown in the figure. For example, the time from NY to St. Louis (or St. Louis to NY) by truck is 30 hours with a standard deviation of 6 hours. In addition, assume that the transfer time in hours in St. Louis is triangularly distributed with parameters (8, 10, 12) for trucks (truck to truck). The transfer time in hours involving rail is triangularly distributed with parameters (13, 15, 17) for rail (rail to rail, rail to truck, truck to rail). We are interested in determining the shortest total shipment time combination from NY to LA. Develop an simulation for this problem.
How many shipment combinations are there?
Write an expression for the total shipment time of the truck only combination.
We are interested in estimating the average shipment time for each shipment combination and the probability that the shipment combination will be able to deliver the shipment within 85 hours.
Estimate the probability that a shipping combination will be the shortest.
Exercise 3.24 A firm produces YBox gaming stations for the consumer market. Their profit function is: \[\text{Profit} = (\text{unit price} - \text{unit cost})\times(\text{quantity sold}) - \text{fixed costs}\]
Suppose that the unit price is $200 per gaming station, and that the other variables have the following probability distributions:
| Unit Cost | 80 | 90 | 100 | 110 |
|---|---|---|---|---|
| Probability | 0.20 | 0.40 | 0.30 | 0.10 |
| Quantity Sold | 1000 | 2000 | 3000 | |
| Probability | 0.10 | 0.60 | 0.30 | |
| Fixed Cost | 50000 | 65000 | 80000 | |
| Probability | 0.40 | 0.30 | 0.30 |
Use a simulation model to generate 1000 observations of the profit. Use stream 1 for the unit cost distribution, stream 2 for the quantity sold distribution, and stream 3 for the fixed cost distribution.
Estimate the mean profit from your sample and compute a 95% confidence interval for the mean profit. Estimate the probability that the profit will be positive.
Exercise 3.25 T. Wilson operates a sports magazine stand before each game. He can buy each magazine for 33 cents and can sell each magazine for 50 cents. Magazines not sold at the end of the game are sold for scrap for 5 cents each. Magazines can only be purchased in bundles of 10. Thus, he can buy 10, 20, and so on magazines prior to the game to stock his stand. The lost revenue for not meeting demand is 17 cents for each magazine demanded that could not be provided. Mr. Wilson’s profit is as follows:
\[\begin{aligned} \text{Profit} & = (\text{revenue from sales}) - (\text{cost of magazines}) \\ & - (\text{lost profit from excess demand}) \\ & + (\text{salvage value from sale of scrap magazines}) \end{aligned} \]
Not all game days are the same in terms of potential demand. The type of day depends on a number of factors including the current standings, the opponent, and whether or not there are other special events planned for the game day weekend. There are three types of game days demand: high, medium, low. The type of day has a probability distribution associated with it.
| Type of Day | High | Medium | Low |
|---|---|---|---|
| Probability | 0.35 | 0.45 | 0.20 |
The amount of demand for magazines then depends on the type of day according to the following distributions:
| Demand | PMF | CDF | PMF | CDF | PMF | CDF |
| 40 | 0.03 | 0.03 | 0.1 | 0.1 | 0.44 | 0.44 |
| 50 | 0.05 | 0.08 | 0.18 | 0.28 | 0.22 | 0.66 |
| 60 | 0.15 | 0.23 | 0.4 | 0.68 | 0.16 | 0.82 |
| 70 | 0.2 | 0.43 | 0.2 | 0.88 | 0.12 | 0.94 |
| 80 | 0.35 | 0.78 | 0.08 | 0.96 | 0.06 | 1.0 |
| 90 | 0.15 | 0.93 | 0.04 | 1.0 | ||
| 100 | 0.07 | 1.0 |
Let \(Q\) be the number of units of magazines purchased (quantity on hand) to setup the stand. Let \(D\) represent the demand for the game day. If \(D > Q\), Mr. Wilson sells only \(Q\) and will have lost sales of \(D-Q\). If \(D < Q\), Mr. Wilson sells only \(D\) and will have scrap of \(Q-D\). Assume that he has determined that \(Q = 50\).
Make sure that you can estimate the average profit and the probability that the profit is greater than zero for Mr. Wilson. Develop a model to estimate the average profit based on 100 observations. Use stream 1 for the type of day distribution and streams 2, 3, 4 for the demand for each type of day.
Exercise 3.26 The time for an automated storage and retrieval system in a warehouse to locate a part consists of three movements. Let \(X\) be the time to travel to the correct aisle. Let \(Y\) be the time to travel to the correct location along the aisle. And let \(Z\) be the time to travel up to the correct location on the shelves. Assume that the distributions of \(X\), \(Y\), and \(Z\) are as follows:
\(X \sim\) lognormal with mean 20 and standard deviation 10 seconds (stream 1)
\(Y \sim\) uniform with minimum 10 and maximum 15 seconds (stream 2)
\(Z \sim\) uniform with minimum of 5 and a maximum of 10 seconds (stream 3)
Develop a model that can estimate the average total time that it takes to locate a part and can estimate the probability that the time to locate a part exceeds 60 seconds. Base your analysis on 1000 observations.
Exercise 3.27 Lead-time demand may occur in an inventory system when the lead-time is other than instantaneous. The lead-time is the time from the placement of an order until the order is received. The lead-time is a random variable. During the lead-time, demand also occurs at random. Lead-time demand is thus a random variable defined as the sum of the demands during the lead-time, or LDT = \(\sum_{i=1}^T D_i\) where \(i\) is the time period of the lead-time and \(T\) is the lead-time. The distribution of lead-time demand is determined by simulating many cycles of lead-time and the demands that occur during the lead-time to get many realizations of the random variable LDT. Notice that LDT is the convolution of a random number of random demands. Suppose that the daily demand for an item is given by the following probability mass function (stream 1):
| Daily Demand (items) | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|
| Probability | 0.10 | 0.30 | 0.35 | 0.10 | 0.15 |
The lead-time is the number of days from placing an order until the firm receives the order from the supplier.
Assume that the lead-time is a constant 10 days. Develop a model to simulate 1000 instances of LDT. Report the summary statistics for the 1000 observations. Estimate the chance that LDT is greater than or equal to 10. Report a 95% confidence interval on your estimate.
Assume that the lead-time has a shifted geometric distribution with probability parameter equal to 0.2 (stream 2). Use a model to simulate 1000 instances of LDT. Report the summary statistics for the 1000 observations. Estimate the chance that LDT is greater than or equal to 10. Report a 95% confidence interval on your estimate.
Exercise 3.28 If \(Z \sim N(0,1)\), and \(Y = \sum_{i=1}^k Z_i^2\) then \(Y \sim \chi_k^2\), where \(\chi_k^2\) is a chi-squared random variable with \(k\) degrees of freedom. Setup a model to generate 50 \(\chi_5^2\) random variates. Report the minimum, maximum, sample average, and 95% confidence interval half-width of the observations. Use stream 1 for your sampling.
Exercise 3.29 Setup a model that will generate 30 observations from the following probability density function using the Acceptance-Rejection algorithm for generating random variates. Use stream 1 for your sampling.
\[f(x) = \begin{cases} \dfrac{3x^2}{2} & -1 \leq x \leq 1\\ 0 & \text{otherwise} \\ \end{cases}\]
Exercise 3.30 This procedure is due to (Box and Muller 1958). Let \(U_1\) and \(U_2\) be two independent uniform (0,1) random variables and define:
\[\begin{aligned} X_1 & = \cos (2 \pi U_2) \sqrt{-2 ln(U_1)}\\ X_2 & = \sin (2 \pi U_2) \sqrt{-2 ln(U_1)}\end{aligned}\]
It can be shown that \(X_1\) and \(X_2\) will be independent standard normal random variables, i.e. \(N(0,1)\). Use to implement the Box and Muller algorithm for generating normal random variables. Generate 1000 \(N(\mu = 2, \sigma = 0.75)\) random variables via this method. Report the minimum, maximum, sample average, and 95% confidence interval half-width of the observations. Assign stream 1 to \(U_1\) and stream 2 \(U_2\).
Exercise 3.31 In the popular English game of Hazard, a player must first determine which of the five numbers from 5-9 will be the “main” point. The player does this by rolling two dice until such time as the point sum equals one of these five numbers. The player then rolls again. He/she wins if the point sum of this roll corresponds with the “main” point as follows: main 5 corresponds with a point sum of 5, main 6 corresponds with a point sum of 6 or 7, main 7 corresponds with sum 7 or 11, main 8 corresponds with sum 8 or 12, and main 9 corresponds with sum 9. The player loses if, having taken on a main point of 5 or 9, he/she then rolls a sum of 11 or 12, or by rolling a sum of 11 against a main of 6 or 8, or by rolling a sum of 12 against a main of 7. In every other situation, the sum thrown becomes the player’s “chance” point. From here on the player rolls two dice until either the “chance” point (player wins) or the “main” point (player loses) reappears.
Using the KSL verify via simulation that the probability of the player winning is equal to 0.5228, where the main and the chance points contribute 0.1910 and 0.3318, respectively, to the probability of winning. Estimate the probabilities to within 4 decimal places of accuracy. Use stream 1 for your sampling.