6.6 The Tie-Dye T-Shirt Model
This section presents another process modeling situation using the KSL. In this modeling situation the key feature to be illustrated is the use of a BlockingQueue to communicate and coordinate between two processes. We will also see that a process can spawn another process.
Example 6.9 (Tie Dye T-Shirts System) Suppose production orders for tie-dye T-shirts arrive to a production facility according to a Poisson process with a mean rate of 1 per hour. There are two basic psychedelic designs involving either red or blue dye. For some reason the blue shirts are a little more popular than the red shirts so that when an order arrives about 70% of the time it is for the blue dye designs. In addition, there are two different package sizes for the shirts, 3 and 5 units. There is a 25% chance that the order will be for a package size of 5 and a 75% chance that the order will be for a package size of 3. Each of the shirts must be individually hand made to the customer’s order design specifications. The time to produce a shirt (of either color) is uniformly distributed within the range of 15 to 25 minutes. There are currently two workers who are setup to make either shirt. When an order arrives to the facility, its type (red or blue) is determined and the pack size is determined. Then, the appropriate number of white (un-dyed) shirts are sent to the shirt makers with a note pinned to the shirt indicating the customer order, its basic design, and the pack size for the order. Meanwhile, the paperwork for the order is processed and a customized packaging letter and box is prepared to hold the order. It takes another worker between 8 to 10 minutes to make the box and print a custom thank you note. After the packaging is made it waits prior to final inspection for the shirts associated with the order. After the shirts are combined with the packaging, they are inspected by the packaging worker which is distributed according to a triangular distribution with a minimum of 5 minutes, a most likely value of 10 minutes, and a maximum value of 15 minutes. Finally, the boxed customer order is sent to shipping.
6.6.1 Implementing the Tie-Dye T-Shirt Model
Before proceeding you might want to jot down your answers to the modeling recipe questions and then you can compare how you are doing with respect to what is presented in this section. The modeling recipe questions are:
What is the system? What information is known by the system?
What are the required performance measures?
What are the entities? What information must be recorded or remembered for each entity? How are entities introduced into the system?
What are the resources that are used by the entities? Which entities use which resources and how?
What are the process flows? Sketch the process or make an activity flow diagram
Develop pseudo-code for the situation
Implement the model
The entities can be conceptualized as the arriving orders. Since the
shirts are processed individually, they should also be considered
entities. In addition, the type of order (red or blue) and the size of
the order (3 or 5) must be tracked. Since the type of the order and the
size of the order are properties of the order, attributes can be used to
model this information. The resources are the two shirt makers and the
packager. The flow is described in the scenario statement: orders
arrive, shirts are made, meanwhile packaging is made. Then, orders are
assembled, inspected, and finally shipped. It should be clear that a
an EntityGenerator can be used to generate Poisson arrivals can create the orders,
but if shirts are entities, how should they be created?
To create the shirts, the order process start the shirt making process based on the size of the order. After this, there will be two types of entities in the model, the orders and the shirts. The shirts can be made and meanwhile the order can be processed. After the shirts for an order are made, they need to be combined together and then matched for the order. This implies that a method is required to uniquely identify the order and coordinating between the processes. This is another piece of information that both the order and the shirt require. Thus, an attribute will be used to note the order number.
The activity diagram for this situation is given in Figure 6.14. After the order is created, the process separates into the order making process and the shirt making process. Notice that the orders and shirts must be synchronized together after each of these processes. In addition, the order making process and the final packaging process share the packager as a resource.
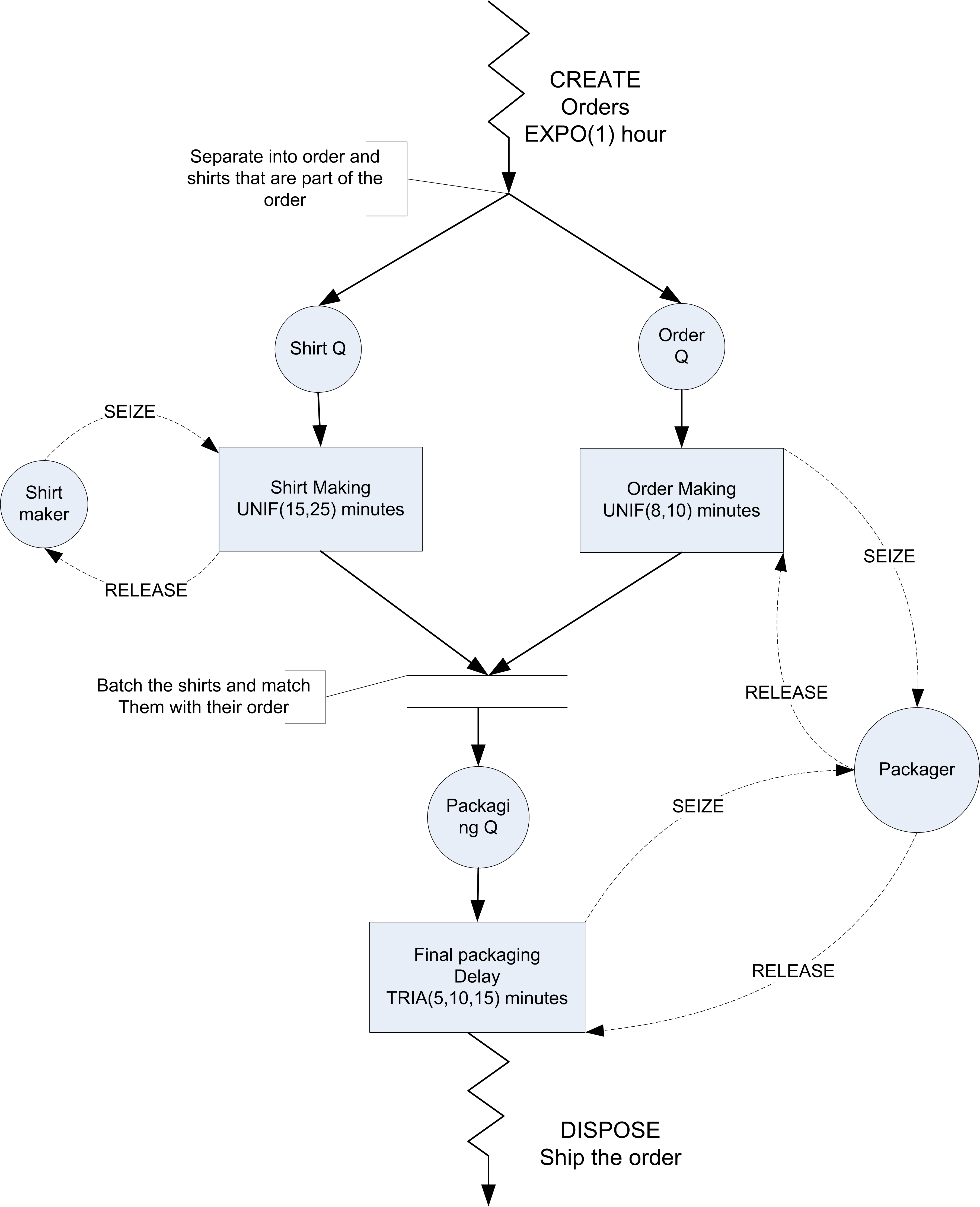
Figure 6.14: Activity diagram for Tie Dye T-Shirts example
Just as in the previous example, you should start by subclassing from ProcessModel and add the necessary random variables and responses. This is illustrated in the following code. In this situation, we use a discrete empirical distribution to model the type and size of the order. The other random variables are straight forward applications of the RandomVariable class. We define two responses to track the total time in the system and the total number of orders in the system.
class TieDyeTShirts(
parent: ModelElement,
name: String? = null
) : ProcessModel(parent, name) {
private val myTBOrders: RVariableIfc = ExponentialRV(60.0)
private val myType: RVariableIfc = DEmpiricalRV(doubleArrayOf(1.0, 2.0), doubleArrayOf(0.7, 1.0))
private val mySize: RVariableIfc = DEmpiricalRV(doubleArrayOf(3.0, 5.0), doubleArrayOf(0.75, 1.0))
private val myOrderSize = RandomVariable(this, mySize)
private val myOrderType = RandomVariable(this, myType)
private val myShirtMakingTime = RandomVariable(this, UniformRV(15.0, 25.0))
private val myPaperWorkTime = RandomVariable(this, UniformRV(8.0, 10.0))
private val myPackagingTime = RandomVariable(this, TriangularRV(5.0, 10.0, 15.0))
private val mySystemTime = Response(this, "System Time")
private val myNumInSystem = TWResponse(this, "Num in System")Now we can develop the process modeling constructs. We will use an EntityGenerator, resources to represent the shirt makers and the packager. Notice that we use a RequestQ to represent the queue for the orders. A RequestQ is a subclass of the Queue class that is specifically designed to work with seize requests for resources. In general, the seize() suspend function allows both the specification of the resource being seized and the queue that will hold the entity if the seize request is not immediately filled. As noted in the activity diagram, there are actually two queues involving the use of the packager. The queue that holds the orders and a queue that holds the completed orders for final packaging. We will see the use of these constructs in the process description. Finally, we use an instance of a BlockingQueue to hold completed shirts and communicate that they are ready.
private val myShirtMakers: ResourceWithQ = ResourceWithQ(this, capacity = 2, name = "ShirtMakers_R")
private val myOrderQ : RequestQ = RequestQ(this, name = "OrderQ")
private val myPackager: ResourceWithQ = ResourceWithQ(this, "Packager_R")
private val generator = EntityGenerator(::Order, myTBOrders, myTBOrders)
private val completedShirtQ: BlockingQueue<Shirt> = BlockingQueue(this, name = "Completed Shirt Q")The order process follows the basic outline of the activity diagram. As we have previously seen, we design a class to represent the orders and the order making process by creating a subclass of the Entity class. Similar to the previous examples, this code uses two properties to hold the type and size of the order and assigns their values based on the random variable instances of the outer class. As note in the code, the type property is never used in the rest of the model; however, it could be useful if we wanted to count the type of shirts produced or for other statistics by type. We also have a list to hold the complete orders. Again, as noted in the code, the list is not really used in a meaningful manner. In this case, it is used to capture the list of items from the waitForItems() function, but not subsequently used. If a future process required the created shirts, then the list could be useful.
private inner class Order: Entity() {
val type: Int = myOrderType.value.toInt() // in the problem, but not really used
val size: Int = myOrderSize.value.toInt()
var completedShirts : List<Shirt> = emptyList() // not really necessary
val orderMaking: KSLProcess = process(isDefaultProcess = true) {
myNumInSystem.increment()
for (i in 1..size) {
val shirt = Shirt(this@Order.id)
activate(shirt.shirtMaking)
}
var a = seize(myPackager, queue = myOrderQ)
delay(myPaperWorkTime)
release(a)
// wait for shirts
completedShirts = waitForItems(completedShirtQ, size, { it.orderNum == this@Order.id })
a = seize(myPackager)
delay(myPackagingTime)
release(a)
myNumInSystem.decrement()
mySystemTime.value = time - this@Order.createTime
}
}When the order making process is activated, there is a for-loop that makes the shirts and activates the shirt making process. This activates the process at the current time. It is important to note that the activated shirt making processes are scheduled to be activated at the current time. Since those events are on the event calendar, they will not be executed until the current event finishes. The current event is essentially the code in the process before the next suspension point. This provides the notion of pseudo-parallelism. The shirt making processes are really pending activation.
Meanwhile, the order continues with its process by using the packager in the classic (seize-delay-release) pattern. However, note the signature of the seize() method, which specifies the queue for waiting orders.
Thus, this use of the packager causes the entity (the order) to wait in the queue for orders. The later seize of the packager cause the order to wait in the pre-defined queue associated with the ResourceWithQ class defined for the packager.
After the paper work is done, the order is ready to start final packaging if it has the shirts associated with the order. This is where the blocking queue is used. The waitForItems() call will be explained more fully shortly. However, at this point, we can think of the order waiting for the correct number of shirts to arrive that are associated with this particular order. After the shirts arrive, the order process continues and again seizes the packager for the packaging time. In this usage of the seize() method, we need only specify an instance of a ResourceWithQ. A ResourceWithQ has a pre-defined RequestQ that holds the requests for the resource. We see that it is simple to share a resource between two different activities. The seize() method also takes in an optional argument that specifies the priority of the seize request. If there are more that one suspending seize() functions that compete for the same resource, you can used the priority parameter to specify which seize request has the priority if more than one is waiting at the same time. Finally, the statistics on the order are collected before its process ends. Now, let’s look at the shirt making process.
private inner class Shirt(val orderNum: Long): Entity() {
val shirtMaking: KSLProcess = process( "Shirt Making"){
val a = seize(myShirtMakers)
delay(myShirtMakingTime)
release(a)
// send to orders
send(this@Shirt, completedShirtQ)
}
}The shirt making process is constructed based on a different entity that represents what happens to a shirt. There are a couple of interesting things to note. First a property orderNum is defined using Kotlin’s concise syntax for declaring properties in the default constructor. The property orderNum is used to identify, for the shirt, which order created it. Then, the shirt uses the shirt makers resource to make the shirt via the (seize-delay-release) code.
Finally, the blocking queue that was defined as part of the process model is used to send a reference to the shirt to the channel queue that connects the shirt process with the ordering process. A Kotlin qualified this reference must be used to identify the shirt within the KSLProcessBuilder. As the shirts are made, they are sent to the channel. When the correct number of shirts for the order are made the waiting order can pull them from the channel and continue with its process. Now, let’s take a closer look at the blocking code statement in the order process:
To understand this code fragment, we need to see some of the implementation of the BlockingQueue class and the suspend functions that are using it. The signature of this method is as follows:
/**
* This method will block (suspend) until the required number of items that meet the criteria
* become available within the blocking queue.
*
* @param blockingQ the blocking queue channel that has the items
* @param amount the number of items needed from the blocking queue that match the criteria
* @param predicate a functional predicate that tests items in the queue for the criteria
* @param blockingPriority the priority associated with the entity if it has to wait to receive
* @param suspensionName the name of the suspension point. can be used to identify which receive suspension point
* the entity is experiencing if there are more than one receive suspension points within the process.
* The user is responsible for uniqueness.
*/
suspend fun <T : ModelElement.QObject> waitForItems(
blockingQ: BlockingQueue<T>,
amount: Int = 1,
predicate: (T) -> Boolean = alwaysTrue,
blockingPriority: Int = KSLEvent.DEFAULT_PRIORITY,
suspensionName: String? = null
): List<T>The first thing to note is the parameter amount. This parameter specifies how many items are being requested from the blocking queue. The next parameter is the predicate. This parameter represents a function that takes in the type being held in the queue and returns true or false depending on some condition. In this case, the type is Shirt. This is a common functional idiom found in functional programming languages such as Kotlin. The predicate is defined as lambda expression that checks if the order number of the shirt it.orderNum is equal to the order number of the current order (this@Order.id). If so, the shirt belongs to the order. Once the specified amount is found within the channel the suspension will end and the ordering process will continue.
Whenever an item is sent to a blocking queue, the blocking queue will check to see if there are any receivers waiting for items. If there are receivers waiting for items, then the blocking queue will use the blocking queue’s request selector to select the next request to be filled. The request is examined to see if it can be filled. That is, the blocking queue checks to see if all the items requested that meet the request criteria are in the queue. In this case, the request criteria is specified by the previously mentioned lambda expression. If the request can be filled, the items are given to the waiting receiver and the receiver’s process can continue.
As discussed in the previous section introducing blocking queues, the default request selector simply looks only at the next waiting request. Other rules for selecting requests can also be provided when configuring the blocking queue. For example, you can provide an instance of a FirstFillableRequest selector as shown in the following code. This class is available as in inner class of BlockingQueue. As can be seen here, this selector will scan the waiting requests and return the first request that can be filled or null if no requests can be filled.
/**
* Allows the next request that can be filled to be selected regardless of its
* location within the request queue.
*/
inner class FirstFillableRequest() : RequestSelectorIfc<T> {
override fun selectRequest(queue: Queue<ChannelRequest>): ChannelRequest? {
for (request in queue) {
if (request.canBeFilled) {
return request
}
}
return null
}
}The results of running the Tie-Dye T-Shirt model indicate that there is substantial waiting done by the order until the shirts are completed.
Half-Width Statistical Summary Report - Confidence Level (95.000)%
Name Count Average Half-Width
-------------------------------------------------------------------------------------
System Time 30 75.4521 7.2003
Num in System 30 1.2393 0.2535
ShirtMakers_R:InstantaneousUtil 30 0.5050 0.0712
ShirtMakers_R:NumBusyUnits 30 1.0100 0.1425
ShirtMakers_R:ScheduledUtil 30 0.5050 0.0712
ShirtMakers_R:WIP 30 2.4023 0.5867
ShirtMakers_R:Q:NumInQ 30 1.3924 0.4646
ShirtMakers_R:Q:TimeInQ 30 21.4801 5.0255
OrderQ:NumInQ 30 0.1870 0.0880
OrderQ:TimeInQ 30 8.9210 5.6039
Packager_R:InstantaneousUtil 30 0.2737 0.0406
Packager_R:NumBusyUnits 30 0.2737 0.0406
Packager_R:ScheduledUtil 30 0.2737 0.0406
Packager_R:WIP 30 0.3958 0.0919
Packager_R:Q:NumInQ 30 0.1221 0.0600
Packager_R:Q:TimeInQ 30 6.8163 2.9580
Completed Shirt Q:RequestQ:NumInQ 30 0.6565 0.1435
Completed Shirt Q:RequestQ:TimeInQ 30 41.6290 5.1649
Completed Shirt Q:ChannelQ:NumInQ 30 1.0645 0.2204
Completed Shirt Q:ChannelQ:TimeInQ 30 20.5181 4.8296
ShirtMakers_R:SeizeCount 30 24.6667 3.4923
Packager_R:SeizeCount 30 14.0333 2.0767
------------------------------------------------------------------------------------