5.7 Comparing System Configurations
The previous sections have concentrated on estimating the performance of a system through the execution of a single simulation model. The running of the model requires the specification of the input variables (e.g. mean time between arrivals, service distribution, etc.) and the structure of the model (e.g. FIFO queue, process flow, etc.) The specification of a set of inputs (variables and/or structure) represents a particular system configuration, which is then simulated to estimate performance. To be able to simulate design configurations, you may have to build different models or you may be able to use the same model supplied with different values of the program inputs. In either situation, you now have different design configurations that can be compared. This allows the performance of the system to be estimated under a wide-variety of controlled conditions. It is this ability to easily perform these what-if simulations that make simulation such a useful analysis tool.
Naturally, when you have different design configurations, you would like to know which configurations are better than the others. Since the simulations are driven by random variables, the outputs from each configuration (e.g. \(Y^1, Y^2\)) are also random variables. The estimate of the performance of each system must be analyzed using statistical methods to ensure that the differences in performance are not simply due to sampling error. In other words, you want to be confident that one system is statistically better (or worse) than the other system.
5.7.1 Comparing Two Systems
The techniques for comparing two systems via simulation are essentially the same as that found in books that cover the statistical analysis of two samples (e.g. (Montgomery and Runger 2006)). This section begins with a review of these methods. Assume that samples from two different populations (system configurations) are available:
\[X_{11}, X_{12},\ldots, X_{1 n_1} \ \ \text{a sample of size $n_1$ from system configuration 1}\]
\[X_{21}, X_{22},\ldots, X_{2 n_2} \ \ \text{a sample of size $n_2$ from system configuration 2}\]
The samples represent a performance measure of the system that will be used in a decision regarding which system configuration is preferred. For example, the performance measure may be the average system throughput per day, and you want to pick the design configuration that has highest throughput.
Assume that each system configuration has an unknown population mean for the performance measure of interest, \(E[X_1] = \theta_1\) and \(E[X_2] = \theta_2\). Thus, the problem is to determine, with some statistical confidence, whether \(\theta_1 < \theta_2\) or alternatively \(\theta_1 > \theta_2\). Since the system configurations are different, an analysis of the situation of whether \(\theta_1 = \theta_2\) is of less relevance in this context.
Define \(\theta = \theta_1 - \theta_2\) as the mean difference in performance between the two systems. Clearly, if you can determine whether \(\theta >\) 0 or \(\theta <\) 0 you can determine whether \(\theta_1 < \theta_2\) or \(\theta_1 > \theta_2\). Thus, it is sufficient to concentrate on the difference in performance between the two systems.
Given samples from two different populations, there are a number of ways in which the analysis can proceed based on different assumptions concerning the samples. The first common assumption is that the observations within each sample for each configuration form a random sample. That is, the samples represent independent and identically distributed random variables. Within the context of simulation, this can be easily achieved for a given system configuration by performing replications. For example, this means that \(X_{11}, X_{12},\ldots, X_{1 n_1}\) are the observations from \(n_1\) replications of the first system configuration. A second common assumption is that both populations are normally distributed or that the central limit theorem can be used so that sample averages are at least approximately normal.
To proceed with further analysis, assumptions concerning the population variances must be made. Many statistics textbooks present results for the case of the population variance being known. In general, this is not the case within simulation contexts, so the assumption here will be that the variances associated with the two populations are unknown. Textbooks also present cases where it is assumed that the population variances are equal. Rather than making that assumption it is better to test a hypothesis regarding equality of population variances.
The last assumption concerns whether or not the two samples can be considered independent of each other. This last assumption is very important within the context of simulation. Unless you take specific actions to ensure that the samples will be independent, they will, in fact, be dependent because of how simulations use (re-use) the same random number streams. The possible dependence between the two samples is not necessarily a bad thing. In fact, under certain circumstance it can be a good thing.
The following sections first presents the methods for analyzing the case of unknown variance with independent samples. Then, we focus on the case of dependence between the samples. Finally, how to use the JSL to do the work of the analysis will be illustrated.
5.7.1.1 Analyzing Two Independent Samples
Although the variances are unknown, the unknown variances are either equal or not equal. In the situation where the variances are equal, the observations can be pooled when developing an estimate for the variance. In fact, rather than just assuming equal or not equal variances, you can (and should) use an F-test to test for the equality of variance. The F-test can be found in most elementary probability and statistics books (see (Montgomery and Runger 2006)).
The decision regarding whether \(\theta_1 < \theta_2\) can be addressed by forming confidence intervals on \(\theta = \theta_1 - \theta_2\). Let \(\bar{X}_1\), \(\bar{X}_2\), \(S_1^2\), and \(S_2^2\) be the sample averages and sample variances based on the two samples (k = 1,2):
\[\bar{X}_k = \dfrac{1}{n_k} \sum_{j=1}^{n_k} X_{kj}\]
\[S_k^2 = \dfrac{1}{n_k - 1} \sum_{j=1}^{n_k} (X_{kj} - \bar{X}_k)^2\]
An estimate of \(\theta = \theta_1 - \theta_2\) is desired. This can be achieved by estimating the difference with \(\hat{D} = \bar{X}_1 - \bar{X}_2\). To form confidence intervals on \(\hat{D} = \bar{X}_1 - \bar{X}_2\) an estimator for the variance of \(\hat{D} = \bar{X}_1 - \bar{X}_2\) is required. Because the samples are independent, the computation of the variance of the difference is:
\[Var(\hat{D}) = Var(\bar{X}_1 - \bar{X}_2) = \dfrac{\sigma_1^2}{n_1} + \dfrac{\sigma_2^2}{n_2}\]
where \(\sigma_1^2\) and \(\sigma_2^2\) are the unknown population variances. Under the assumption of equal variance, \(\sigma_1^2 = \sigma_2^2 =\sigma^2\), this can be written as:
\[Var(\hat{D}) = Var(\bar{X}_1 - \bar{X}_2) = \dfrac{\sigma_1^2}{n_1} + \dfrac{\sigma_2^2}{n_2} = \sigma^2 (\dfrac{1}{n_1} + \dfrac{1}{n_2})\]
where \(\sigma^2\) is the common unknown variance. A pooled estimator of \(\sigma^2\) can be defined as:
\[S_p^2 = \dfrac{(n_1 - 1)S_1^2 + (n_2 - 1)S_2^2}{n_1 + n_2 - 2}\]
Thus, a (\(1 - \alpha\))% confidence interval on \(\theta = \theta_1 - \theta_2\) is:
\[\hat{D} \pm t_{\alpha/2 , v} s_p \sqrt{\dfrac{1}{n_1} + \dfrac{1}{n_2}}\]
where \(v = n_1 + n_2 - 2\). For the case of unequal variances, an approximate (\(1 - \alpha\))% confidence interval on \(\theta = \theta_1 - \theta_2\) is given by:
\[\hat{D} \pm t_{\alpha/2 , v} \sqrt{S_1^2/n_1 + S_2^2/n_2}\]
where \[v = \Biggl\lfloor \frac{(S_1^2/n_1 + S_2^2/n_2)^2}{\frac{(S_1^2/n_1)^2}{n_1 +1} + \frac{(S_2^2/n_2)^2}{n_2 + 1}} - 2 \Biggr\rfloor\]
Let \([l, u]\) be the resulting confidence interval where \(l\) and \(u\) represent the lower and upper limits of the interval with by construction \(l < u\). Thus, if \(u < 0\), you can conclude with (\(1 - \alpha\))% confidence that \(\theta = \theta_1 - \theta_2 < 0\) (i.e. that \(\theta_1 < \theta_2\)). If \(l > 0\), you can conclude with (\(1 - \alpha\))% that \(\theta = \theta_1 - \theta_2 > 0\) (i.e. that \(\theta_1 > \theta_2\)). If \([l, u]\) contains 0, then no conclusion can be made at the given sample sizes about which system is better. This does not indicate that the system performance is the same for the two systems. You know that the systems are different. Thus, their performance will be different. This only indicates that you have not taken enough samples to detect the true difference. If sampling is relatively cheap, then you may want to take additional samples in order to discern an ordering between the systems.
Two configurations are under consideration for the design of an airport security checkpoint. A simulation model of each design was made. The replication values of the throughput per minute for the security station for each design are provided in the following table.
| Design 1 | Design 2 | |
|---|---|---|
| 1 | 10.98 | 8.93 |
| 2 | 8.87 | 9.82 |
| 3 | 10.53 | 9.27 |
| 4 | 9.40 | 8.50 |
| 5 | 10.10 | 9.63 |
| 6 | 10.28 | 9.55 |
| 7 | 8.86 | 9.30 |
| 8 | 9.00 | 9.31 |
| 9 | 9.99 | 9.23 |
| 10 | 9.57 | 8.88 |
| 11 | 8.05 | |
| 12 | 8.74 | |
| \(\bar{x}\) | 9.76 | 9.10 |
| \(s\) | 0.74 | 0.50 |
| \(n\) | 10 | 12 |
Assume that the two simulations were run independently of each other, using different random numbers. Recommend the better design with 95% confidence.
According to the results:
\[\hat{D} = \bar{X}_1 - \bar{X}_2 = 9.76 - 9.1 = 0.66\]
In addition, we should test if the variances of the samples are equal. This requires an \(F\) test, with \(H_0: \sigma_{1}^{2} = \sigma_{2}^{2}\) versus \(H_1: \sigma_{1}^{2} \neq \sigma_{2}^{2}\). Based on elementary statistics, the test statistic is: \(F_0 = S_{1}^{2}/S_{1}^{2}\). The rejection criterion is to reject \(H_0\) if \(F_0 > f_{\alpha/2, n_1-1, n_2 -1}\) or \(F_0 < f_{1-\alpha/2, n_1-1, n_2 -1}\), where \(f_{p, u, v}\) is the upper percentage point of the \(F\) distribution. Assuming a 0.01 significance level for the \(F\) test, we have \(F_0 = (0.74)^{2}/(0.50)^{2} = 2.12\). Since \(f_{0.005, 9, 11} = 5.54\) and \(f_{0.995, 9, 11} = 0.168\), there is not enough evidence to conclude that the variances are different at the 0.01 significance level. The value of \(f_{p, u, v}\) can be determined in as F.INV.RT(p, u, v). Note also that \(f_{1-p, u, v} = 1/f_{p, v, u}\). In \(R\), the formula is \(f_{p, u, v} = qt(1-p, u,v)\), since \(R\) provides the quantile function, not the upper right tail function.
Since the variances can be assumed equal, we can use the pooled variance, which is:
\[\begin{aligned} S_p^2 & = \dfrac{(n_1 - 1)S_1^2 + (n_2 - 1)S_2^2}{n_1 + n_2 - 2}\\ & = \dfrac{(10 - 1)(0.74)^2 + (12 - 1)(0.5)^2}{12 + 10 - 2} \\ & = 0.384\end{aligned}\]
Thus, a (\(1 -0.05\))% confidence interval on \(\theta = \theta_1 - \theta_2\) is:
\[\begin{aligned} \hat{D} & \pm t_{\alpha/2 , v} s_p \sqrt{\dfrac{1}{n_1} + \dfrac{1}{n_2}} \\ 0.66 & \pm t_{0.025 , 20} (\sqrt{0.384}) \sqrt{\dfrac{1}{10} + \dfrac{1}{12}} \\ 0.66 & \pm (2.086)(0.6196)(0.428) \\ 0.66 & \pm 0.553\end{aligned}\]
where \(v = n_1 + n_2 - 2 = 10 + 12 - 2 = 20\). Since this results in an interval \([0.10, 1.21]\) that does not contain zero, we can conclude that design 1 has the higher throughput with 95% confidence.
The confidence interval can assist in making decisions regarding relative performance of the systems from a statistically significant standpoint. However, if you make a conclusion about the ordering of the system, it still may not be practically significant. That is, the difference in the system performance is statistically significant but the actual difference is of no practical use. For example, suppose you compare two systems in terms of throughput with resulting output \(\bar{X}_1\) = 5.2 and \(\bar{X}_2\) = 5.0 with the difference statistically significant. While the difference of 0.2 may be statistically significant, you might not be able to achieve this in the actual system. After all, you are making a decision based on a model of the system not on the real system. If the costs of the two systems are significantly different, you should prefer the cheaper of the two systems since there is no practical difference between the two systems. The fidelity of the difference is dependent on your modeling assumptions. Other modeling assumptions may overshadow such a small difference.
The notion of practical significance is model and performance measure dependent. One way to characterize the notion of practical significance is to conceptualize a zone of performance for which you are indifferent between the two systems.
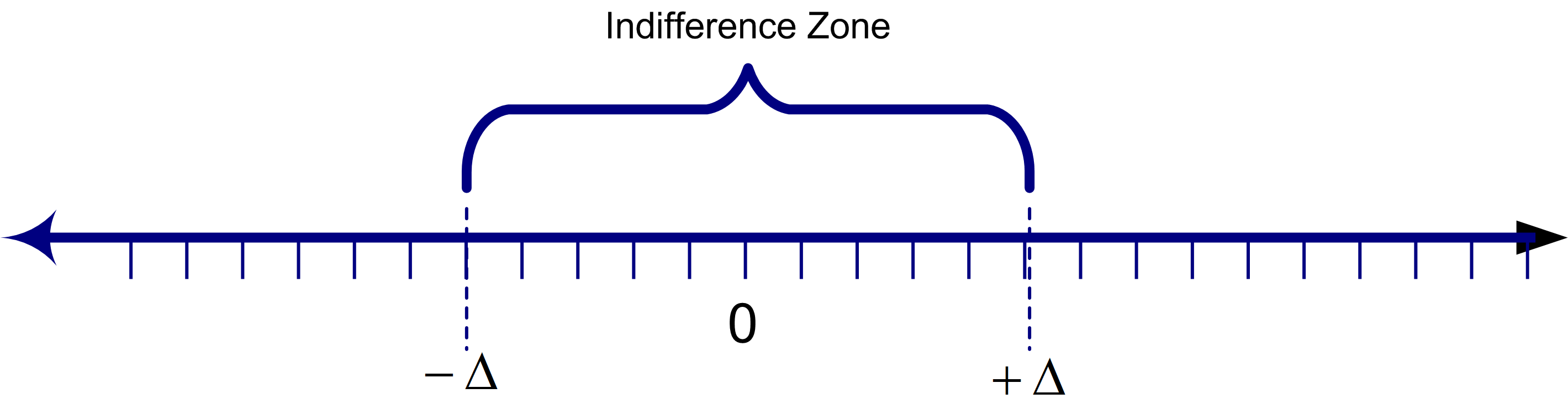
Figure 5.21: Indifference Zone Concept
Figure 5.21 illustrates the concept of an indifference zone around the difference between the two systems. If the difference between the two systems falls in this zone, you are indifferent between the two systems (i.e. there is no practical difference).
Using the indifference zone to model the notion of practical significance, if \(u < -\Delta\), you can conclude confidence that \(\theta_1 < \theta_2\), and if \(l > \Delta\), you can conclude with confidence that \(\theta_1 > \theta_2\). If \(l\) falls within the indifference zone and \(u\) does not (or vice versa), then there is not enough evidence to make a confident conclusion. If \([l,u]\) is totally contained within the indifference zone, then you can conclude with confidence that there is no practical difference between the two systems.
5.7.1.2 Analyzing Two Dependent Samples
In this situation, continue to assume that the observations within a sample are independent and identically distributed random variables; however, the samples themselves are not independent. That is, assume that the \((X_{11}, X_{12},\ldots, X_{1n_1})\) and \((X_{21}, X_{22}, \ldots, X_{2n_2})\) from the two systems are dependent.
For simplicity, suppose that the difference in the configurations can be implemented using a simple parameter change within the model. For example, the mean processing time is different for the two configurations. First, run the model to produce \((X_{11}, X_{12}, \ldots, X_{1n_1})\) for configuration 1. Then, change the parameter and re-executed the model to produce \((X_{21}, X_{22}, \ldots, X_{2n_2})\) for configuration 2.
Assuming that you did nothing with respect to the random number streams, the second configuration used the same random numbers that the first configuration used. Thus, the generated responses will be correlated (dependent). In this situation, it is convenient to assume that each system is run for the same number of replications, i.e. \(n_1\) = \(n_2\) = n. Since each replication for the two systems uses the same random number streams, the correlation between \((X_{1,j}, X_{2,j})\) will not be zero; however, each pair will still be independent across the replications. The basic approach to analyzing this situation is to compute the difference for each pair:
\[D_j = X_{1j} - X_{2j} \ \ \text{for} \; j = 1,2,\ldots,n\]
The \((D_1, D_2, \ldots, D_n)\) will form a random sample, which can be analyzed via traditional methods. Thus, a (\(1 - \alpha\))% confidence interval on \(\theta = \theta_1 - \theta_2\) is:
\[\bar{D} = \dfrac{1}{n} \sum_{j=1}^n D_j\]
\[S_D^2 = \dfrac{1}{n-1} \sum_{j=1}^n (D_j - \bar{D})^2\]
\[\bar{D} \pm t_{\alpha/2, n-1} \dfrac{S_D}{\sqrt{n}}\]
The interpretation of the resulting confidence interval \([l, u]\) is the same as in the independent sample approach. This is the paired-t confidence interval presented in statistics textbooks.
Assume that the two simulations were run dependently using common random numbers. Recommend the better design with 95% confidence.
Assume that the two simulations were run dependently using common random numbers. Recommend the better design with 95% confidence.
| Design 1 | Design 2 | Difference | |
|---|---|---|---|
| 1 | 52.56 | 49.92 | 2.64 |
| 2 | 48.77 | 47.08 | 1.69 |
| 3 | 53.49 | 50.62 | 2.87 |
| 4 | 50.60 | 48.45 | 2.15 |
| 5 | 51.60 | 49.20 | 2.40 |
| 6 | 51.77 | 49.33 | 2.44 |
| 7 | 51.09 | 48.81 | 2.27 |
| 8 | 53.51 | 50.64 | 2.88 |
| 9 | 47.44 | 46.08 | 1.36 |
| 10 | 47.94 | 46.45 | 1.48 |
| \(\bar{x}\) | 50.88 | 48.66 | 2.22 |
| \(s\) | 2.18 | 1.64 | 0.55 |
| \(n\) | 10 | 10 | 10 |
According to the results:
\[\bar{D} = \bar{X}_1 - \bar{X}_2 = 50.88 - 48.66 = 2.22\]
Also, we have that \(S_D^2 = (0.55)^2\). Thus, a (\(1 -0.05\))% confidence interval on \(\theta = \theta_1 - \theta_2\) is:
\[\begin{aligned} \hat{D} & \pm t_{\alpha/2, n-1} \dfrac{S_D}{\sqrt{n}}\\ 2.22 & \pm t_{0.025 , 9} \dfrac{0.55}{\sqrt{10}}\\ 2.22 & \pm (2.261)(0.1739)\\ 2.22 & \pm 0.0.393\end{aligned}\]
Since this results in an interval \([1.827, 2.613]\) that does not contain zero, we can conclude that design 1 has the higher throughput with 95% confidence.
Of the two approaches (independent versus dependent) samples, the latter is much more prevalent in simulation contexts. The approach is called the method of common random numbers (CRN) and is a natural by product of how most simulation languages handle their assignment of random number streams.
To understand why this method is the preferred method for comparing two systems, you need to understand the method’s affect on the variance of the estimator. In the case of independent samples, the estimator of performance was \(\hat{D} = \bar{X}_1 - \bar{X}_2\). Since
\[\begin{aligned} \bar{D} & = \dfrac{1}{n} \sum_{j=1}^n D_j \\ & = \dfrac{1}{n} \sum_{j=1}^n (X_{1j} - X_{2j}) \\ & = \dfrac{1}{n} \sum_{j=1}^n X_{1j} - \dfrac{1}{n} \sum_{j=1}^n X_{2j} \\ & = \bar{X}_1 - \bar{X}_2 \\ & = \hat{D}\end{aligned}\]
The two estimators are the same, when \(n_1 = n_2 = n\); however, their variances are not the same. Under the assumption of independence, computing the variance of the estimator yields:
\[V_{\text{IND}} = Var(\bar{X}_1 - \bar{X}_2) = \dfrac{\sigma_1^2}{n} + \dfrac{\sigma_2^2}{n}\]
Under the assumption that the samples are not independent, the variance of the estimator is:
\[V_{\text{CRN}} = Var(\bar{X}_1 - \bar{X}_2) = \dfrac{\sigma_1^2}{n} + \dfrac{\sigma_2^2}{n} - 2\text{cov}(\bar{X}_1, \bar{X}_2)\]
If you define \(\rho_{12} = corr(\bar{X}_1, \bar{X}_2)\), the variance for the common random number situation is:
\[V_{\text{CRN}} = V_{\text{IND}} - 2\sigma_1 \sigma_2 \rho_{12}\]
Therefore, whenever there is positive correlation \(\rho_{12} > 0\) within the pairs we have that, \(V_{\text{CRN}} < V_{\text{IND}}\).
If the variance of the estimator in the case of common random numbers is smaller than the variance of the estimator under independent sampling, then a variance reduction has been achieved. The method of common random numbers is called a variance reduction technique. If the variance reduction results in a confidence interval for \(\theta\) that is tighter than the independent case, the use of common random numbers should be preferred. The variance reduction needs to be big enough to overcome any loss in the number of degrees of freedom caused by the pairing. When the number of replications is relatively large (\(n > 30\)) this will generally be the case since the student-t value does not vary appreciatively for large degrees of freedom. Notice that the method of common random numbers might backfire and cause a variance increase if there is negative correlation between the pairs. An overview of the conditions under which common random numbers may work is given in (Law 2007).
This notion of pairing the outputs from each replication for the two system configurations makes common sense. When trying to discern a difference, you want the two systems to experience the same randomness so that you can more readily infer that any difference in performance is due to the inherent difference between the systems and not caused by the random numbers.
In experimental design settings, this is called blocking on a factor. For example, if you wanted to perform and experiment to determine whether a change in a work method was better than the old method, you should use the same worker to execute both methods. If instead, you had different workers execute the methods, you would not be sure if any difference was due to the workers or to the proposed change in the method. In this context, the worker is the factor that should be blocked. In the simulation context, the random numbers are being blocked when using common random numbers.
5.7.1.3 Using Common Random Numbers
The following explores how independent sampling and common random
numbers can be implemented using the KSL. To illustrate this situation, we will utilize the familiar pallet processing example. For this situation, we will compare the performance of the system based on the time to process all pallets using two and three workers. The following code will demonstrate how to get the results based on not using common random number and based on using common random numbers. To facilitate this analysis we will use a KSLDatabaseObserver and the resulting KSLDatabase to capture the output from the simulations. In addition, we will use the MultipleComparisonAnalyzer class found in the ksl.utilities.statistics package to tabulate and compute the paired difference results. Based on our previous work with the pallet processing model, the code is very straight-forward. The following function executes the model twice. In the code, we make sure to assign different names to the experiments before running them. Of course, the number of workers is also changed. The code executes both simulation experiments sequentially and the results are stored in the KSL database.
fun withoutCommonRandomNumbers(){
val model = Model("Pallet Model Experiments")
model.numberOfReplications = 30
// add the model element to the main model
val palletWorkCenter = PalletWorkCenter(model)
// use a database to capture the response data
val kslDatabaseObserver = KSLDatabaseObserver(model)
model.experimentName = "Two Workers"
palletWorkCenter.numWorkers = 2
model.simulate()
model.experimentName = "Three Workers"
palletWorkCenter.numWorkers = 3
model.simulate()
val responseName = palletWorkCenter.totalProcessingTime.name
val db = kslDatabaseObserver.db
val expNames = listOf("Two Workers", "Three Workers")
val comparisonAnalyzer = db.multipleComparisonAnalyzerFor(expNames, responseName)
println(comparisonAnalyzer)
}Notice the second to last line of the code where we use the instance of the KSLDatabase to create an instance of the MultipleComparisonAnalyzer class based on the names of the experiments and the name of the response variable to be compared. The MultipleComparisonAnalyzer has a significant amount of output, part of which is shown here.
Statistical Summary Report
Difference Data
Name Count Average Std. Dev.
----------------------------------------------------------------------------------------------------
Two Workers - Three Workers 30 64.7723 57.8792
----------------------------------------------------------------------------------------------------
95.0% Confidence Intervals on Difference Data
Two Workers - Three Workers [43.15986335728935, 86.38476883829914]We should note the sample standard deviation on the difference, \(s_d = 57.8792\). Since the confidence interval does not contain zero, we can conclude with 95% confidence that the system with two workers has a longer time to complete the processing of the pallets. Of course, this result should be expected.
Because the simulation experiments were executed sequentially within the same invocation of the program, the random number streams in the three worker simulation continued from where the streams ended for the two worker simulation. Thus, the two experiments used different underlying random numbers and can be considered as independent sampling. To utilize common random numbers we must manipulate the streams. The following code illustrates how to implement common random numbers within the KSL.
Example 5.6 (Performing a CRN Analysis) This code example illustrates how to perform a common random number analysis for two systems by running them within the same execution frame and setting the reset start stream option to true.
fun withCommonRandomNumbers(){
val model = Model("Pallet Model Experiments")
model.numberOfReplications = 30
// add the model element to the main model
val palletWorkCenter = PalletWorkCenter(model)
// use a database to capture the response data
val kslDatabaseObserver = KSLDatabaseObserver(model)
model.resetStartStreamOption = true
model.experimentName = "Two Workers"
palletWorkCenter.numWorkers = 2
model.simulate()
model.experimentName = "Three Workers"
palletWorkCenter.numWorkers = 3
model.simulate()
val responseName = palletWorkCenter.totalProcessingTime.name
val db = kslDatabaseObserver.db
val expNames = listOf("Two Workers", "Three Workers")
val comparisonAnalyzer = db.multipleComparisonAnalyzerFor(expNames, responseName)
println(comparisonAnalyzer)
}The only difference between this code and the previous code is the addition of line 9:
This line tells the model to automatically reset the streams of all of the random variables (and other constructs that use streams) back to their starting point in their stream prior to executing the replications of the experiment. This causes the three worker simulation to start in the streams in the same location as the two worker simulation. This facilitates the syncronization of the use of the random numbers. In addition, there are two other methods that the KSL automatically performs to assist in syncronization. First, each random variable utilizes its own dedicated stream, by default, and secondly, at the end of each replication, the random number streams are advanced (automatically) to the next substream in their main stream. This ensures that every replication starts in the same place in the streams. The effect of common random numbers on variance reduction can be dramatic. The results for this situation are as follows:
Statistical Summary Report
Difference Data
Name Count Average Std. Dev.
---------------------------------------------------------------------------------
Two Workers - Three Workers 30 64.9215 33.0561
---------------------------------------------------------------------------------
95.0% Confidence Intervals on Difference Data
Two Workers - Three Workers [52.57814571744155, 77.26483056807177]We see the that the sample standard deviation on the difference, \(s_d = 33.0561\) for the case of common random numbers has been significantly reduced (about a 43% reduction in this case). What does this mean for the simulation analyst? First the confidence interval half-width will also be shortened. Thus, we have a tighter margin of error for the same confidence level. This may be more important when the results are closer and when it takes significantly longer to execute the models. That is, we get more precision on the estimate of the difference for no extra computing.
It is important to note that setting the reset start stream option to true as indicated here is predicated on running both models in the same program execution. If we had run the two worker model today and then changed the number of workers to 3 for a run tomorrow, the simulations would have used the same random number streams (common random numbers by default). If we had saved the results in the database and reattached the same database to the execution, we would capture the results from both runs (just like we did in this example). Thus, we would still have used common random numbers. You need to be careful if you take this approach not to over write your earlier results by properly utilizing the KSL database functionality.
5.7.2 Concepts for Comparing Systems
The analysis of multiple systems stems from a number of objectives. First, you may want to perform a sensitivity analysis on the simulation model. In a sensitivity analysis, you want to measure the effect of small changes to key input parameters to the simulation. For example, you might have assumed a particular arrival rate of customers to the system and want to examine what would happen if the arrival rate decreased or increased by 10%. Sensitivity analysis can help you to understand how robust the model is to variations in assumptions. When you perform a sensitivity analysis, there may be a number of factors that need to be examined in combination with other factors. This may result in a large number of experiments to run. Besides performing a sensitivity analysis, you may want to compare the performance of multiple alternatives in order to choose the best alternative. This type of analysis is performed using multiple comparison statistical techniques. This section will also illustrate how to perform a multiple comparison with some of the constructs of the KSL.
Suppose that you are interested in analyzing \(k\) systems based on performance measures \(\theta_i, \, i = 1,2, \ldots, k\). The goals may be to compare each of the \(k\) systems with a base case (or existing system), to develop an ordering among the systems, or to select the best system. In any case, assume that some decision will be made based on the analysis and that the risk associated with making a bad decision needs to be controlled. In order to perform an analysis, each \(\theta_i\) must be estimated, which results in sampling error for each individual estimate of \(\theta_i\). The decision will be based upon all the estimates of \(\theta_i\) (for every system). The the sampling error involves the sampling for each configuration. This compounds the risk associated with an overall decision. To see this more formally, the “curse” of the Bonferroni inequality needs to be understood.
The Bonferroni inequality states that given a set of (not necessarily independent) events, \(E_i\), which occur with probability, \(1-\alpha_i\), for \(i = 1,2,\ldots, k\) then a lower bound on the probability of the intersection of the events is given by:
\[P \lbrace \cap_{i=1}^k E_i \rbrace \geq 1 - \sum_{i=1}^k \alpha_i\]
In words, the Bonferroni inequality states that the probability of all the events occurring is at least one minus the sum of the probability of the individual events occurring. This inequality can be applied to confidence intervals, which are probability statements concerning the chance that the true parameter falls within intervals formed by the procedure.
Suppose that you have \(c\) confidence intervals each with confidence \(1-\alpha_i\). The \(i^{th}\) confidence interval is a statement \(S_i\) that the confidence interval procedure will result in an interval that contains the parameter being estimated. The confidence interval procedure forms intervals such that \(S_i\) will be true with probability \(1-\alpha_i\). If you define events, \(E_i = \lbrace S_i \text{is true}\rbrace\), then the intersection of the events can be interpreted as the event representing all the statements being true.
\[P\lbrace \text{all} \, S_i \, \text{true}\rbrace = P \lbrace \cap_{i=1}^k E_i \rbrace \geq 1 - \sum_{i=1}^k \alpha_i = 1 - \alpha_E\]
where \(\alpha_E = \sum_{i=1}^k \alpha_i\). The value \(\alpha_E\) is called the overall error probability. This statement can be restated in terms of its complement event as:
\[P\lbrace \text{one or more} \, S_i \, \text{are false} \rbrace \leq \alpha_E\]
This gives an upper bound on the probability of a false conclusion based on the procedures that generated the confidence intervals.
This inequality can be applied to the use of confidence intervals when comparing multiple systems. For example, suppose that you have, \(c = 10\), 90% confidence intervals to interpret. Thus, \(\alpha_i = 0.10\), so that
\[\alpha_E = \sum_{i=1}^{10} \alpha_i = \sum_{i=1}^{10} (0.1) = 1.0\]
Thus, \(P\lbrace \text{all} \, S_i \, \text{true}\rbrace \geq 0\) or \(P\lbrace\text{one or more} \, S_i \, \text{are false} \rbrace \leq 1\). In words, this is implying that the chance that all the confidence intervals procedures result in confidence intervals that cover the true parameter is greater than zero and less than 1. Think of it this way: If your boss asked you how confident you were in your decision, you would have to say that your confidence is somewhere between zero and one. This would not be very reassuring to your boss (or for your job!).
To combat the “curse” of Bonferroni, you can adjust your confidence levels in the individual confidence statements in order to obtain a desired overall risk. For example, suppose that you wanted an overall confidence of 95% on making a correct decision based on the confidence intervals. That is you desire, \(\alpha_E\) = 0.05. You can pre-specify the \(\alpha_i\) for each individual confidence interval to whatever values you want provided that you get an overall error probability of \(\alpha_E = 0.05\). The simplest approach is to assume \(\alpha_i = \alpha\). That is, use a common confidence level for all the confidence intervals. The question then becomes: What should \(\alpha\) be to get \(\alpha_E\) = 0.05? Assuming that you have \(c\) confidence intervals, this yields:
\[\alpha_E = \sum_{i=1}^c \alpha_i = \sum_{i=1}^c \alpha = c\alpha\]
So that you should set \(\alpha = \alpha_E/c\). For the case of \(\alpha_E = 0.05\) and \(c = 10\), this implies that \(\alpha = 0.005\). What does this do to the width of the individual confidence intervals? Since the \(\alpha_i = \alpha\) have gotten smaller, the confidence coefficient (e.g. \(z\) value or \(t\) value) used in computation of the confidence interval will be larger, resulting in a wider confidence interval. Thus, you must trade-off your overall decision error against wider (less precise) individual confidence intervals.
Because the Bonferroni inequality does not assume independent events it can be used for the case of comparing multiple systems when common random numbers are used. In the case of independent sampling for the systems, you can do better than simply bounding the error. For the case of comparing \(k\) systems based on independent sampling the overall confidence is:
\[P \lbrace \text{all}\, S_i \, \text{true}\rbrace = \prod_{i=1}^c (1 - \alpha_i)\]
If you are comparing \(k\) systems where one of the systems is the standard (e.g. base case, existing system, etc.), you can reduce the number of confidence intervals by analyzing the difference between the other systems and the standard. That is, suppose system one is the base case, then you can form confidence intervals on \(\theta_1 - \theta_i\) for \(i = 2,3,\ldots, k\). Since there are \(k - 1\) differences, there are \(c = k - 1\) confidence intervals to compare.
If you are interested in developing an ordering between all the systems, then one approach is to make all the pair wise comparisons between the systems. That is, construct confidence intervals on \(\theta_j - \theta_i\) for \(i \neq j\). The number of confidence intervals in this situation is
\[c = \binom{k}{2} = \frac{k(k - 1)}{2}\]
The trade-off between overall error probability and the width of the individual confidence intervals will become severe in this case for most practical situations.
Because of this problem a number of techniques have been developed to allow the selection of the best system (or the ranking of the systems) and still guarantee an overall pre-specified confidence in the decision. Multiple comparison procedures are described in (Goldsman and Nelson 1998) and the references therein. See also (Law 2007) for how these methods relate to other ranking and selection methods.
5.7.3 Multiple Comparison with the Best Procedures (MCB)
While it is beyond the scope of this textbook to review multiple comparison with the best (MCB) procedures, it is useful to have a basic understanding of the form of the confidence interval constructed by these procedures. To see how MCB procedures avoid part of the issues with having a large number of confidence intervals, we can note that the confidence interval is based on the difference between the best and the best of the rest. Suppose we have \(k\) system configurations to compare and suppose that somehow you knew that the \(i^{th}\) system is the best. Now, consider a confidence interval for system’s \(i\) performance metric, \(\theta_i\), of the following form:
\[ \theta_i - \max_{j \neq i} \theta_j \] This difference is the difference between the best (\(\theta_i\)) and the second best. This is because if \(\theta_i\) is the best, when we find the maximum of those remaining, it will be next best (i.e. second best). Now, let us suppose that system \(i\) is not the best. Reconsider, \(\theta_i - \max_{j \neq i} \theta_j\). Then, this difference will represent the difference between system \(i\), which is not the best, and the best of the remaining systems. In this case, because \(i\) is not the best, the set of systems considered in \(\max_{j \neq i} \theta_j\) will contain the best. Therefore, in either case, this difference:
\[ \theta_i - \max_{j \neq i} \theta_j \] tells us exactly what we want to know. This difference allows us to compare the best system with the rest of the best. MCB procedures build \(k\) confidence intervals:
\[ \theta_i - \max_{j \neq i} \theta_j \ \text{for} \ i=1,2, \dots,k \] Therefore, only \(k\) confidence intervals need to be considered to determine the best rather than, \(\binom{k}{2}\).
This form of confidence interval has also been combined with the concept of an indifference zone. Indifference zone procedures use a parameter \(\delta\) that indicates that the decision maker is indifferent between the performance of two systems, if the difference is less than \(\delta\). This indicates that even if there is a difference, the difference is not practically significant to the decision maker within this context. These procedures attempt to ensure that the overall probability of correct selection of the best is \(1-\alpha\), whenever, \(\theta_{i^{*}} - \max_{j \neq i^{*}} \theta_j > \delta\), where \(i^{*}\) is the best system and \(\delta\) is the indifference parameter. This assumes that larger is better in the decision making context. There are a number of single stage and multiple stage procedures that have been developed to facilitate decision making in this context.
One additional item of note to consider when using these procedures. The results may not be able to distinguish between the best and others. For example, assuming that we desire the maximum (bigger is better), then let \(\hat{i}\) be the index of the system found to be the largest and let \(\hat{\theta}_{i}\) be the estimated performance for system \(i\), then, these procedures allow the following:
- If \(\hat{\theta}_{i} - \hat{\theta}_{\hat{i}} + \delta \leq 0\), then we declare that system \(i\) not the best.
- If \(\hat{\theta}_{i} - \hat{\theta}_{\hat{i}} + \delta > 0\), then we can declare that system \(i\) is not statistically different from the best. In this case, system \(i\), may in fact be the best.
The computations necessary to perform many different multiple comparision procedures can be found in the MultipleComparisonAnalyzer class illustrated in Figure 5.22.
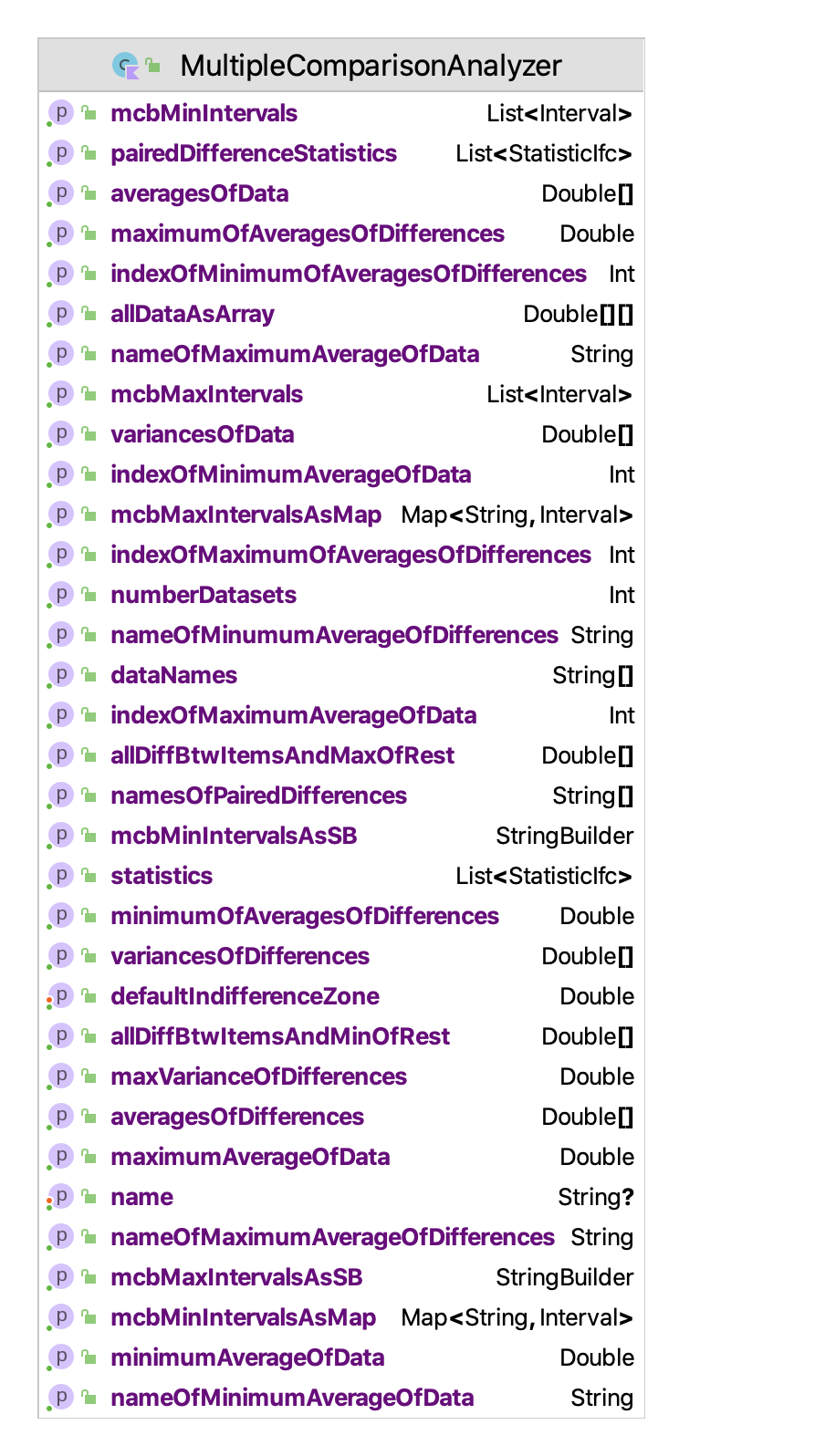

Figure 5.22: Properties and Methods of the MultipleComparisonAnalyzer Class
The MultipleComparisonAnalyzer class depends on having the data to be compared in the form of named arrays within a map dataMap: Map<String, DoubleArray>. Each array is associated with the name of the array via the map’s key parameter. There needs to be at least 2 data arrays, and the length of each data array must be the same. As we have seen in the previous example, the KSL facilitates extracting and organizing the simulation data in this form from the KSL database. Such data can also be readily extracted from instances of a ReplicationDataObserver or an ExperimentDataObserver. The following code illustrates setting up a MultipleComparisonAnalyzer based on arrays.
fun main() {
val data = LinkedHashMap<String, DoubleArray>()
val d1 = doubleArrayOf(63.72, 32.24, 40.28, 36.94, 36.29, 56.94, 34.10, 63.36, 49.29, 87.20)
val d2 = doubleArrayOf(63.06, 31.78, 40.32, 37.71, 36.79, 57.93, 33.39, 62.92, 47.67, 80.79)
val d3 = doubleArrayOf(57.74, 29.65, 36.52, 35.71, 33.81, 51.54, 31.39, 57.24, 42.63, 67.27)
val d4 = doubleArrayOf(62.63, 31.56, 39.87, 37.35, 36.65, 57.15, 33.30, 62.21, 47.46, 79.60)
data["One"] = d1
data["Two"] = d2
data["Three"] = d3
data["Four"] = d4
val mca = MultipleComparisonAnalyzer(data)
println(mca)
}The MultipleComparisonAnalyzer class will automatically compute the following:
- statistical summaries and confidence intervals on the individual data arrays
- statistical summaries and confidence intervals on all pair-wise differences
- the variance of the difference that is the largest
- the data set that has the smallest average and its average
- the data set that has the largest average and its average
- the pair-wise difference that is the smallest and its value
- the pair-wise difference that is the largest and its value
- multiple comparison confidence intervals based on finding the maximum value
- multiple comparison confidence intervals based on finding the minimum value
- screening intervals for best designs by constructing subsets containing the best configuration
The user can specify the indifference zone parameter to be included in the confidence interval calculations. The MultipleComparisonAnalyzer class does not utilize the probability of correct selection or assume some underlying distribution. The confidence intervals that are computed have the following forms. Define \(Y_{ij}\) as the \(i^{th}\) observation of system \(j\). Thus, \(\bar{Y}_{\cdot j}\) is the mean performance of system \(j\). Let \(\delta\) be the indifference zone parameter. When selecting the system with the largest \(\bar{Y}_{\cdot j}\) as the best, the confidence intervals for configurations \(i=1,2,\dots,k\) are computed by:
\(\min\{0, \bar{Y}_{\cdot j} - \max_{j \neq i}\bar{Y}_{\cdot j}- \delta \} \leq \theta_i - \max_{j \neq i} \theta_j \leq \max\{0, \bar{Y}_{\cdot j} - \max_{j \neq i}\bar{Y}_{\cdot j}- \delta \}\)
When selecting the system with the smallest \(\bar{Y}_{\cdot j}\) as the best, the confidence intervals for configurations \(i=1,2,\dots,k\) are computed by:
\(\min\{0, \bar{Y}_{\cdot j} - \min_{j \neq i}\bar{Y}_{\cdot j}- \delta \} \leq \theta_i - \max_{j \neq i} \theta_j \leq \max\{0, \bar{Y}_{\cdot j} - \min_{j \neq i}\bar{Y}_{\cdot j}- \delta \}\)
The results for the example code previously discussed illustrate the form of these confidence intervals.
MCB Maximum Intervals
Indifference delta: 0.0
Name Interval
One [0.0, 0.7999999999999972]
Two [-0.7999999999999972, 0.0]
Three [-5.686000000000007, 0.0]
Four [-1.2579999999999956, 0.0]
MCB Minimum Intervals
Indifference delta: 0.0
Name Interval
One [0.0, 5.686000000000007]
Two [0.0, 4.88600000000001]
Three [-4.4280000000000115, 0.0]
Four [0.0, 4.4280000000000115]Notice how the form of these confidence interval equations require that for the case of finding the maximum, systems that are candidates for the maximum have a lower interval limit of 0.0, while candidate systems that should be ruled out have an upper limit of 0.0. The reverse is true for the case of finding the minimum. Also, note that the confidence intervals (as defined here) do not have a distribution requirement for computing a test statistic value. Thus, their forms do not depend on the distributional assumptions. However, the probability of correctly selecting the best will depend upon some distributional assumptions. If the confidence interval contains zero, then it cannot be ruled out as the best. When this occurs, it is advisable to increase the sample size to see if a clear winner emerges.
Further details of such procedures can be found in (Goldsman and Nelson 1998). As a note, some of those procedures require the computation of critical values from the multivariate \(T\) distribution and Rinott’s constant. Rinott’s constant can be computed using the Rinott class within the ksl.utilities.statistics package and limited values for the multivariate \(T\) distribution are available via the MultipleComparisonAnalyzer class’s companion object. Finally, the quantiles of the Tukey distribution are available via the Tukey class located in the ksl.utilities.distributions package.
To illustrate the application of MCB methods, let us consider the two-stage Bonferroni based procedure developed by (Matejcik and Nelson 1995) and also described in (Goldsman and Nelson 1998) as well as in (Banks et al. 2005). This presentation follows the one in (Banks et al. 2005). To apply the procedure, the analyst specifies a probability of correct selection (PCS) as \((1-\alpha)\) and performs the experimentation in two-stages. The first stage is essentially a pilot set of replications from which the variability of the design configurations is estimated and used to plan the second stage of the procedure. The procedure is applicable when the data is normally distributed and can be applied if the observations are independent or if CRN has been used.
Two-Stage Bonferroni Procedure
Specify the indifference parameter, \(\delta\), PCS as \((1-\alpha)\), the initial sample size, \(n_0\), and compute \(t= t_{1-\alpha/(k-1),n_0 - 1}\)
Execute the \(n_0\) replications for each system and capture \(Y_{ij}\) as the \(i^{th}\) observation of system \(j\)
Compute \(\bar{Y}_{\cdot j}\) as the mean performance of system \(j\), for \(j=1,2,\cdots,k\). Then for all \(i \neq j\), compute the sample variance of the differences and the largest sample variance \(\hat{S}^2 = max_{i \neq j}S^{2}_{ij}\)
\[\begin{equation} S^{2}_{ij} = \frac{1}{n_0 - 1} \sum_{r=1}^{n_0} ((Y_{ri} - Y_{rj}) - (\bar{Y}_{\cdot i} - \bar{Y}_{\cdot j}))^2 \end{equation}\]
- Calculate the second stage sample size:
\[\begin{equation} n = max \Bigl\{ n_0, \Bigl \lceil \frac{t^2\hat{S}^2}{\delta^2} \Bigr \rceil \Bigr\} \end{equation}\]
Make \(n - n_0\) additional replications (or just make \(n\) by re-running). Capture \(Y_{ij}\) as the \(i^{th}\) observation of system \(j\)
Calculate the overall sample means for \(j=1, 2,\cdots, k\) for each design.
\[\begin{equation} \bar{Y}_{\cdot j} = \frac{1}{n}\sum_{r=1}^{n}Y_{rj} \end{equation}\]
- Select the system with the largest \(\bar{Y}_{\cdot j}\) as the best and if maximizing form the confidence intervals:
\(\min\{0, \bar{Y}_{\cdot j} - \max_{j \neq i}\bar{Y}_{\cdot j}- \delta \} \leq \theta_i - \max_{j \neq i} \theta_j \leq \max\{0, \bar{Y}_{\cdot j} - \max_{j \neq i}\bar{Y}_{\cdot j}- \delta \}\)
If minimizing, form the confidence intervals:
\(\min\{0, \bar{Y}_{\cdot j} - \min_{j \neq i}\bar{Y}_{\cdot j}- \delta \} \leq \theta_i - \max_{j \neq i} \theta_j \leq \max\{0, \bar{Y}_{\cdot j} - \min_{j \neq i}\bar{Y}_{\cdot j}- \delta \}\)
The MultipleComparisonAnalyzer class automatically computes everything that is needed to apply the Two-Stage Bonferroni procedure. The toString() method can be used to see all the results. The second stage sample size can be computed via the function secondStageSampleSizeNM(), and the maximum variance can be found from property, maxVarianceOfDifferences. In addition, the maximum or minimum performer can be noted from the nameOfMaximumAverageOfData and nameOfMinimumAverageOfData properties. The respective performance of the maximum and minimum via the maximumAverageOfData and minimumAverageOfData properties. Finally, the MCB intervals for each case are found from the mcbMaxIntervals(delta) and mcbMinIntervals(delta) functions respectively. Note that if \(n = n_0\) in step 5, then no additional replications are required and the PCS will still be met. (Matejcik and Nelson 1995) recommend that the initial number of replications in the first stage should be greater than or equal to 10 (\(n_0 \geq 10\)). The two-stage Bonferroni procedure is somewhat conservative in recommending the sample size requirements. If the number of replications is of concern, then the reader should consult (Banks et al. 2005) for other procedures.
The following KSL code illustrates the basic use of the MultipleComparisonAnalyzer class on some data.
fun main() {
val data = LinkedHashMap<String, DoubleArray>()
data["One"] = doubleArrayOf(63.72, 32.24, 40.28, 36.94, 36.29, 56.94, 34.10, 63.36, 49.29, 87.20)
data["Two"] = doubleArrayOf(63.06, 31.78, 40.32, 37.71, 36.79, 57.93, 33.39, 62.92, 47.67, 80.79)
data["Three"] = doubleArrayOf(57.74, 29.65, 36.52, 35.71, 33.81, 51.54, 31.39, 57.24, 42.63, 67.27)
data["Four"] = doubleArrayOf(62.63, 31.56, 39.87, 37.35, 36.65, 57.15, 33.30, 62.21, 47.46, 79.60)
val mca = MultipleComparisonAnalyzer(data)
val out = PrintWriter(System.out, true)
mca.writeDataAsCSVFile(out)
out.println()
println(mca)
println("num data sets: " + mca.numberDatasets)
println(mca.dataNames.contentToString())
val r = mca.secondStageSampleSizeNM(2.0, 0.95)
println("Second stage sampling recommendation R = $r")
}The output from the running of the code contains everything you need for a MCB analysis.
Multiple Comparison Report: Statistical Summary Report
Raw Data
Name Count Average Std. Dev.
---------------------------------------------------------------
One 10 50.0360 17.7027
Two 10 49.2360 16.2450
Three 10 44.3500 13.1509
Four 10 48.7780 15.9415
--------------------------------------------------------------
95.0% Confidence Intervals on Data
One [37.37228240333723, 62.69971759666277]
Two [37.61502264027472, 60.85697735972529]
Three [34.94237884397989, 53.7576211560201]
Four [37.37412553653087, 60.18187446346914]
Statistical Summary Report
Difference Data
Name Count Average Std. Dev.
-----------------------------------------------------------------------
One - Two 10 0.8000 2.1208
One - Three 10 5.6860 5.3384
One - Four 10 1.2580 2.3430
Two - Three 10 4.8860 3.4435
Two - Four 10 0.4580 0.3445
Three - Four 10 -4.4280 3.1384
-----------------------------------------------------------------------
95.0% Confidence Intervals on Difference Data
One - Two [-0.717163895232598, 2.317163895232595]
One - Three [1.8671698996711696, 9.504830100328828]
One - Four [-0.41806967690470764, 2.934069676904709]
Two - Three [2.422703009361264, 7.349296990638738]
Two - Four [0.21155519141551002, 0.7044448085844948]
Three - Four [-6.673063053959199, -2.182936946040797]
Max variance = 28.498048888888913
Min performer = Three
Min performance = 44.349999999999994
Max performer = One
Max performance = 50.036
Min difference = Three - Four
Min difference value = -4.427999999999998
Max difference = One - Three
Max difference value = 5.685999999999999
MCB Maximum Intervals
Indifference delta: 0.0
Name Interval
One [0.0, 0.7999999999999972]
Two [-0.7999999999999972, 0.0]
Three [-5.686000000000007, 0.0]
Four [-1.2579999999999956, 0.0]
MCB Minimum Intervals
Indifference delta: 0.0
Name Interval
One [0.0, 5.686000000000007]
Two [0.0, 4.88600000000001]
Three [-4.4280000000000115, 0.0]
Four [0.0, 4.4280000000000115]
num data sets: 4
[One, Two, Three, Four]
Second stage sampling recommendation R = 455.7.4 Screening Procedures
Assuming that the data are normally distributed (with or without CRN), screening procedures can be designed to select a subset of the system designs such that the retained subset will contain the true best system with probability greater than \(1-\alpha\). Such procedures are useful when there are a large number of designs or during automated search procedures. Once a reliable subset has been found then MCB procedures can be used to select the best from the designated subset. The following screening procedure is based on (Nelson et al. 2001).
- Step 1: Specify the PCS as \((1-\alpha)\), a common sample size, \(n \ge 2\), and compute \(t= t_{1-\alpha/(k-1),n - 1}\)
- Step 2: Execute the \(n\) replications for each system and capture \(Y_{ij}\) as the \(i^{th}\) observation of system \(j\)
- Step 3: Compute \(\bar{Y}_{\cdot j}\) as the mean performance of system \(j\), for \(j=1,2,\cdots,k\). Then for all \(i \neq j\), compute the sample variance of the differences:
\[ S^{2}_{ij} = \frac{1}{n_0 - 1} \sum_{r=1}^{n_0} ((Y_{ri} - Y_{rj}) - (\bar{Y}_{\cdot i} - \bar{Y}_{\cdot j}))^2 \]
- Step 4: If bigger is better, then place system \(i\) in the selection subset if for all \(j \ne i\): \[ \bar{Y}_{\cdot i} \ge \bar{Y}_{\cdot j} - t \frac{S_{ij}}{\sqrt{n}} \] If smaller is better, then place system \(i\) in the selection subset if for all \(j \ne i\): \[ \bar{Y}_{\cdot i} \le \bar{Y}_{\cdot j} + t \frac{S_{ij}}{\sqrt{n}} \]
Suppose we want to apply the screening procedure to the pairwise comparison data and assume that smaller is better. The screening procedure essentially says to add the system to the subset of remaining alternatives if its sample average is smaller than all the other sample means that have been adjusted by a positive quantity that accounts for sampling error. In the pairwise difference data, we have \(\bar{Y}_{\cdot i}\) and \(S_{ij}\).
Let’s take a look at a simplified example. Note that \(\hat{se}_{ij} = S_{ij}/\sqrt{n}\). If smaller is better, then place system \(i\) in the selection subset if for all \(j \ne i\), \(\bar{Y}_{\cdot i} \le \bar{Y}_{\cdot j} + t * \hat{se}_{ij}\). In this example suppose \(k=4\), \(\alpha = 0.05\), \(n=10\), \(t= t_{1-\alpha/(k-1),n - 1} = 2.5096\). In the following the sample average for system 1, \(\bar{Y}_{\cdot 1} = 50.036\) is compared to the computed upper limits for all the other configurations.
\[ \begin{aligned} \bar{Y}_{\cdot 1} = 50.036 & \overset{?}{\le} \bar{Y}_{\cdot 2} + t * \hat{se}_{12} = 49.236 + 2.5096 \times 0.6707=50.9191\\ & \overset{?}{\le} \bar{Y}_{\cdot 3} + t * \hat{se}_{13} = 44.35 + 2.5096 \times 1.6881 = 48.5865\\ & \overset{?}{\le} \bar{Y}_{\cdot 4} + t * \hat{se}_{14} = 48.778 + 2.5096 \times 0.7409 = 50.6374\\ \end{aligned} \]
Note that system 1 fails to be less than all the limits. Thus, system 1 is eliminated. This calculation is continued for all the systems to form the subset holding the remaining systems that were not eliminated during the screening process.
To apply the MultipleComparisonAnalyzer class on a KSL simulation, we can just attach a KSLDatabaseObserver instance and ask for the MultipleComparisonAnalyzer instance as illustrated in the following code for the pallet model.
Example 5.7 (Performing a MCB Analysis) In this KSL code example, three configurations are compared using CRN and MCB.
fun main() {
val model = Model("Pallet Model MCB")
// add the model element to the main model
val palletWorkCenter = PalletWorkCenter(model)
// use a database to capture the response data
val kslDatabaseObserver = KSLDatabaseObserver(model)
// simulate the model
model.experimentName = "One Worker"
palletWorkCenter.numWorkers = 1
model.resetStartStreamOption = true
model.numberOfReplications = 30
model.simulate()
model.experimentName = "Two Workers"
palletWorkCenter.numWorkers = 2
model.simulate()
model.experimentName = "Three Workers"
palletWorkCenter.numWorkers = 3
model.simulate()
val responseName = palletWorkCenter.totalProcessingTime.name
val db = kslDatabaseObserver.db
val expNames = listOf("One Worker","Two Workers", "Three Workers")
val comparisonAnalyzer = db.multipleComparisonAnalyzerFor(expNames, responseName)
println(comparisonAnalyzer)
}It should be obvious that 3 workers results in the smallest total processing time. Notice in the screening output that the 3 worker case is the only system that passes all the screening tests.
MCB Minimum Intervals
Indifference delta: 0.0
Name Interval
One Worker [0.0, 517.7287463179446]
Two Workers [0.0, 64.92148814275674]
Three Workers [-64.92148814275674, 0.0]
Min Screening Intervals
One Worker average = 943.8223691355911 Two Workers [-Infinity, 499.44125093353716]
One Worker average = 943.8223691355911 Three Workers [-Infinity, 444.40016711694113]
Two Workers average = 491.0151109604032 One Worker [-Infinity, 952.2485091087251]
Two Workers average = 491.0151109604032 Three Workers [-Infinity, 438.43696524296155]
Three Workers average = 426.09362281764646 One Worker [-Infinity, 962.1289134348857]
Three Workers average = 426.09362281764646 Two Workers [-Infinity, 503.3584533857183]
Alternatives remaining after screening for minimum:
[Three Workers]