5.8 Simulating Many Scenarios
As illustrated in the previous section, there is often a need to simulate many variations of the same or different models and capture the results for further analysis. This section provides an overview of the KSL constructs that facilitate the running of many scenarios. The primary purpose of this section is to explain the built in constructs and illustrate their use within simple examples. In most realistic situations, the models will have more complex input and output mapping than illustrated in this section. The illustrated constructs can be readily scaled up to larger models and more complex situations, perhaps even running models in parallel computing environments. However, this section only presents the basic use case. We start by understanding controls and how to manage the parameters of random variables.
5.8.1 Control Annotations
Because simulation models may have many types of inputs variables that may need to be changed by the modeler, the KSL defines an access protocol based on Kotlin property variables that have been annotated to define them as a controllable variable. The annotations provide meta-data about the KSL model element that can be used to define a generic protocol for setting the values of the properties prior to running a simulation model. This functionality is implemented in the ksl.controls package.
The KSLControl annotation can be used on the setter method of properties within model elements to indicate that those properties can be used to control the execution of the simulation model. The annotation field type must be supplied and must be one of the valid control types as specified by the enum ControlType. The user is responsible for making sure that the type field matches (or is consistent with) the type of the property. Even though the optional annotation fields (lowerBound and upperBound) are specified as double values, they will be converted to an appropriate value for the specified type. Boolean properties are represented as a 1.0 (true) and 0.0 (false) within the numerical conversion for the controls. If a control is BOOLEAN, then the user can supply a 1.0 to represent true and a 0.0 to represent false when setting the control, which will then be set to true or false, appropriately. Current control types include (Double, Int, Long, Short, Byte, Float) and Boolean. In essence, the numeric types are all represented as a Double with appropriate conversions occurring when the property is assigned.
The PalletWorkCenter model that has been illustrated in this chapter has an annotated property for control. In the follow code, we see the Kotlin annotation syntax @set:KSLControl to annotate the numWorkers property for the PalletWorkCenter model.
@set:KSLControl(
controlType = ControlType.INTEGER,
lowerBound = 1.0
)
var numWorkers = numWorkers
set(value) {
require(value >= 1) { "The number of workers must be >= 1" }
require(!model.isRunning) { "Cannot change the number of workers while the model is running!" }
field = value
}The annotation KSLControl has been defined with properties controlType, name, lowerBound, upperBound, comment, and include. The most important properties are controlType and the bounds. By default the bounds are positive and negative infinity. In the example code for the numWorker property the lower bound has been specified as 1.0 to indicate that the value of this property cannot be less than 1.0. The control type of ControlType.INTEGER ensures that even though the control’s value is specified as a Double, the supplied value will be converted to an Int when it is applied. This approach simplifies the specification of parameter values.
Model elements can have many properties that have been annotated as a KSLControl. For example, the initial value property for a Variable has been annotated as follows.
@set:KSLControl(
controlType = ControlType.DOUBLE
)
override var initialValue: Double = theInitialValue
set(value) {
require(domain.contains(value)) { "The initial value, $value must be within the specified range for the variable: $domain" }
if (model.isRunning) {
Model.logger.info { "The user set the initial value during the replication. The next replication will use a different initial value" }
}
field = value
}These annotations indicate in a generic manner which properties can be controllable. When you develop your own model elements, you can take advantage of the generic access protocol and build interesting ways to set the controls of your models. In what follows, we will illustrate how to use controls.
The Model class has a controls() function that returns all of the controls associated with every model element within a model. The following code illustrates how to access the controls for a model and print out their key values.
Example 5.8 (Illustrating a Control) The following example code illustrates how to access a control and change its value, resulting in the change of the associated property.
fun main() {
val model = Model("Pallet Model MCB")
// add the model element to the main model
val palletWorkCenter = PalletWorkCenter(model, name ="PWC")
println("Original value of property:")
println("num workers = ${palletWorkCenter.numWorkers}")
println()
val controls = model.controls()
println("Control keys:")
for (controlKey in controls.controlKeys()) {
println(controlKey)
}
// find the control with the desired key
val control = controls.control("PWC.numWorkers")!!
// set the value of the control
control.value = 3.0
println()
println("Current value of property:")
println("num workers = ${palletWorkCenter.numWorkers}")
}This results in the following output.
Original value of property:
num workers = 2
Control keys:
PWC.numWorkers
NumBusyWorkers.initialValue
PalletQ:NumInQ.initialValue
Num Pallets at WC.initialValue
Num Processed.initialCounterLimit
Num Processed.initialValue
P{total time > 480 minutes}.initialValue
Current value of property:
num workers = 3The important aspect of this output to notice are the keys associated with the controls. The numWorkers property associated with the PalletWorkCenter class has the key PWC.numWorkers. The PWC portion of the key has been derived from the assigned name of the created instance of the PalletWorkCenter class. Since the name of the model element is unique and the Kotlin property name numWorkers must be unique, this combination is unique and can be used to look up the control associated with the annotated property.
The second aspect of this example is the fact that prior to setting the control, the underlying numWorkers property had a value of 2.0. Then, after accessing the control and changing its value, the numWorkers property value was updated to 3.0. Now, this is a bit of overkill for changing the value of a single property; however, this illustrates the basic mechanics of using controls. Because the key for a control is unique, as long as you know the associated key you can change the value of the associated property via its associated control. A more useful use case would be to store the key-value pairs in a file and read in the new values of the properties from the file. Then, a generic procedure can be written to change all the controls.
5.8.2 Random Variable Parameters
Stochastic simulation models use random variables. Thus, it is common to need to change the values of the parameters associated with the random variables when running experiments. The architecture of the KSL with respect to random variables can be somewhat daunting. The key issue is that changing out the random variable or its parameters requires careful methods because random variables are immutable and changing their values must ensure that replications start with same settings (so that they are truly replicates). The second complicating factor is that the number of parameters associated with random variables varies widely by type of random variable. For example, an exponential random variable has one parameter, its mean, while a triangular random variable has three parameters (min, mode, max). Because of these challenges, the KSL provides a generic protocol for accessing and changing the parameter values of every random variable associated with a KSL model. This is accomplished via the RVParameterSetter class and its associated supporting classes within the ksl.rvariable.parameters package. This section will provide a brief overview of how to utilize this generic protocol for changing the parameters associated with the random variables of a KSL model.
Example 5.9 (Changing Random Variable Parameters) The following example code illustrates how to access the parameters of a random variable and how to apply the change within the model.
fun main() {
val model = Model("Pallet Model MCB")
// add the model element to the main model
val palletWorkCenter = PalletWorkCenter(model, name ="PWC")
println(palletWorkCenter.processingTimeRV)
val tmpSetter = RVParameterSetter(model)
val map = tmpSetter.rvParameters
println()
println("Standard Map Representation:")
for ((key, value) in map) {
println("$key -> $value")
}
val rv = map["ProcessingTimeRV"]!!
rv.changeDoubleParameter("mode", 14.0)
tmpSetter.applyParameterChanges(model)
println()
println(palletWorkCenter.processingTimeRV)
}Similar to how controls function, the parameters associated with a model can be retrieved by creating an instance of the RVParameterSetter class. The RVParameterSetter class has many representations of the parameters associated with random variables within the model. An instance of the RVParameterSetter class holds a map that uses the name of the random variable from the model as the key and returns an instance of the RVParameters class. The RVParameters class holds information about the parameters of the random variable based on their types (Double, Int, DoubleArray). Currently the RVParameterSetter class only holds random variables that have integer or double type parameters.
In the code example, first the string representation of the random variable is printed. We can see from the output that its name is ProcessingTimeRV and its underlying source of randomness is a triangular distributed random variable with minimum 8, mode 12, and maximum 15, using stream 3. The returned map of random variable parameters is used to get the RVParameters associated with the ProcessingTimeRV and then the mode parameter is changed to the value of 14.
ModelElement{Class Name=RandomVariable, Id=4, Name='ProcessingTimeRV', Parent Name='PWC, Parent ID=3, Model=Pallet_Model_MCB}
Initial random Source: TriangularRV(min=8.0, mode=12.0, max=15.0) with stream 3
Standard Map Representation:
Pallet_Model_MCB:DefaultUniformRV -> RV Type = Uniform
Double Parameters {min=0.0, max=1.0}
ProcessingTimeRV -> RV Type = Triangular
Double Parameters {min=8.0, mode=12.0, max=15.0}
TransportTimeRV -> RV Type = Exponential
Double Parameters {mean=5.0}
NumPalletsRV -> RV Type = Binomial
Double Parameters {probOfSuccess=0.8, numTrials=100.0}
ModelElement{Class Name=RandomVariable, Id=4, Name='ProcessingTimeRV', Parent Name='PWC, Parent ID=3, Model=Pallet_Model_MCB}
Initial random Source: TriangularRV(min=8.0, mode=14.0, max=15.0) with stream 3Then the code, applies the parameter change to the model. It is important to note that changing parameter value in the map does not change the parameter in the model. The change is only applied to the model when the applyParameterChanges() function is invoked. As we can see from the printed output for the associated random variable, the mode has been updated to 14. As was the case for controls, changing individual parameter values via this generic protocol is a bit of overkill for a single parameter. However, this protocol defines a general approach that will work as long as you know the name of the random variable within the model and the name of the parameter to change. The code prints out the map relationship from which you can easily make note of the associated names of the random variables and the names of their defined parameters.
The RVParameterSetter class also has a flattened structure for holding parameter values similar to how controls work. The name of the random variable is concatenated with its associated parameter name to form a unique key. The following code illustrates this representation.
val flatMap = tmpSetter.flatParametersAsDoubles
println("Flat Map Representation:")
for ((key, value) in flatMap) {
println("$key -> $value")
}The resulting print out of the map is show here.
Flat Map Representation:
Pallet_Model_MCB:DefaultUniformRV.min -> 0.0
Pallet_Model_MCB:DefaultUniformRV.max -> 1.0
ProcessingTimeRV.min -> 8.0
ProcessingTimeRV.mode -> 14.0
ProcessingTimeRV.max -> 15.0
TransportTimeRV.mean -> 5.0
NumPalletsRV.probOfSuccess -> 0.8
NumPalletsRV.numTrials -> 100.0Notice that the name of the processing time random variable ProcessingTimeRV has been concatenated with its parameter names min, mode, and max. This representation is useful for storing controls and random variable parameters within the same file or data structure for generic processing.
5.8.3 Setting Up and Running Multiple Scenarios
This section puts the concepts presented in the last two sections into practice by illustrating how to construct scenarios and how to execute the scenarios.
The code found in Example 5.7 has a very common pattern.
- create a model and its elements
- set up the model
- simulate the model
- create another model or change the previous model’s parameters
- simulate the model
- repeat for each experimental configuration
Within the KSL these concepts have been generalized by providing the Scenario class and the ScenarioRunner class. A scenario represents the specification of a model to run, with some inputs. Each scenario will produce a simulation run (SimulationRun). The naming of a scenario is important. The name of the scenario should be unique within the context of running multiple scenarios with a ScenarioRunner instance. The name of the scenario is used to assign the name of the model’s experiment. If the scenario names are unique, then the experiment names will be unique. In the context of running multiple scenarios, it is important that the experiment names be unique to permit automated storage within the associated KSL database.
The following code presents the constructor of a scenario. Notice that the key parameters of the constructor are a model, a map of inputs, and the name of the scenario. The input map represents (key, value) pairs specifying controls or random variable names (in flat map form) along with its assigned value.
class Scenario(
val model: Model,
name: String,
inputs: Map<String, Double> = emptyMap(),
numberReplications: Int = model.numberOfReplications,
lengthOfReplication: Double = model.lengthOfReplication,
lengthOfReplicationWarmUp: Double = model.lengthOfReplicationWarmUp,
) : Identity(name), ExperimentIfc by model {
...Once a scenario is defined, a list of scenarios can be provided to the ScenarioRunner class. The purpose of the ScenarioRunner class is to facilitate the batch running of all the defined scenarios and the collection of the simulation results from the scenarios into a KSLDatabase instance. Let’s take a look at how to use the ScenarioRunner class.
Example 5.10 (Using a ScenarioRunner) In this code example, we see that an instance of the ScenarioRunner class can be used to run many scenarios. The loop after running the scenarios is simply for the purpose of displaying the results.
The buildScenarios() function is simply a function that returns a list of scenarios. This is where the real magic happens. The first thing to note about the following code is that scenarios can be defined on the same or different models. It makes no difference to the ScenarioRunner class whether the scenarios are related to one or more models. The ScenarioRunner will simply execute all the scenarios that it is supplied. In the following code, the PalletWorkCenter model is again used in the illustration as one of the scenario models. Here, maps of inputs using the controls and random variable parameters, are used to configure the inputs to three different scenarios. For illustrative purposes only, a fourth scenario is created and configured using the drive through pharmacy model.
fun buildScenarios() : List<Scenario> {
val model = Model("Pallet Model", autoCSVReports = true)
// add the model element to the main model
val palletWorkCenter = PalletWorkCenter(model, name = "PWC")
// set up the model
model.resetStartStreamOption = true
model.numberOfReplications = 30
val sim1Inputs = mapOf(
"ProcessingTimeRV.mode" to 14.0,
"PWC.numWorkers" to 1.0,
)
val sim2Inputs = mapOf(
"ProcessingTimeRV.mode" to 14.0,
"PWC.numWorkers" to 2.0,
)
val sim3Inputs = mapOf(
"ProcessingTimeRV.mode" to 14.0,
"PWC.numWorkers" to 3.0,
)
val dtpModel = Model("DTP Model", autoCSVReports = true)
dtpModel.numberOfReplications = 30
dtpModel.lengthOfReplication = 20000.0
dtpModel.lengthOfReplicationWarmUp = 5000.0
val dtp = DriveThroughPharmacyWithQ(dtpModel, name = "DTP")
val sim4Inputs = mapOf(
"DTP.numPharmacists" to 2.0,
)
val s1 = Scenario(model = model, inputs = sim1Inputs, name = "One Worker")
val s2 = Scenario(model = model, inputs = sim2Inputs, name = "Two Worker")
val s3 = Scenario(model = model, inputs = sim3Inputs, name = "Three Worker")
val s4 = Scenario(model = dtpModel, inputs = sim4Inputs, name = "DTP_Experiment")
return listOf(s1, s2, s3, s4)
}WARNING! When configuring the scenarios do not forget to specify the model’s experimental run parameters. That is, make sure to provide the run length, number of replications, and the warm up period (if needed). This can be achieved by setting the parameters of the model or by providing the values when constructing a scenario.
The running of the many scenarios will produce much output. The resulting output from running the code from Example 5.10 in shown is Figure 5.23.
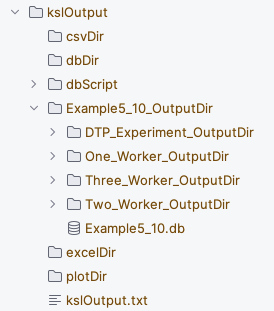
Figure 5.23: Output from Running Scenarios
We see from Figure 5.23 that an output directory is created having the name of the ScenarioRunner instance associated with it. Within that output directory is an output directory for each of the scenarios. In addition, for this example, a KSL database has been created, Example5_10.db, which holds all of the simulation results from the scenario runs. As we can see from the constructor of the ScenarioRunner class, a property is available to access the KSL database within code. As previously illustrated in Example 5.7 the KSL database reference could be used to create a MultipleComparisonAnalyzer instance and perform a MCB analysis. Or as illustrated in Section 5.4.1, the database can be used to access the statistical results and export results to CSV (or Excel) files.
class ScenarioRunner(
name: String,
scenarioList: List<Scenario> = emptyList(),
val pathToOutputDirectory: Path = KSL.createSubDirectory(name.replace(" ", "_") + "_OutputDir"),
val kslDb: KSLDatabase = KSLDatabase("${name}.db".replace(" ", "_"), pathToOutputDirectory)
) : Identity(name) {Also, the properties scenarioList and scenariosByName allow access to the scenarios. The scenarioList property was used in illustrating the output from the scenarios as per the code in Example 5.10.
BTW
Configuring a scenario based on only controls and random variable parameters may be difficult for complex models. Because of this the Scenario class has a property called setup which can hold a reference to a functional interface ScenarioSetupIfc that can be supplied and executed prior to simulating the scenario.
By supplying a setup function, you can invoke any logic that you need to configure the model prior to simulating the scenario.
As you can see, the KSL provides functionality to run many scenarios and collect the statistical results associated with the scenarios with a simple to use protocol.