7.1 Modeling with Processes and Resources
In this section, we explore some of the nuances of modeling systems via process and resources. Specifically, we will look more carefully at the KSL constructs for modeling resources. In general, a resource is something that is required or used by the entities within a process. In real systems, whenever there is requirement for an entity to wait, it is likely that a resource is needed. Within the KSL, a resource has number of identical units which represent its capacity. For the purposes of usage, the units of the resource are indistinguishable. That is, there can be no requirement to use one of the units over some other of the units. For the entity, it does not matter which unit is supplied for a request. It only matters that it gets the requested number of units from the resource. Resource units are allocated and deallocated to entities that request them. If a request for a specific number of units of the resource cannot be allocated immediately upon request, then the entity (generally) must wait for the units (or not proceed with the request). If there is a preference between types of resources, then a pool of resources should be used. Pools of resources will also be discussed in this section. We begin our study of resources by illustrating how resources can be used to model space.
7.1.1 Modeling Space with Resources
We start the modeling of space with resources by looking at a simple system involving a tandem queue. A tandem queue is a sequence of queues in order that must be visited to receive service from resources. Let’s setup the situation by first modeling the system without a space requirement between the queues. The following example presents the specifics of the situation.
Example 7.1 (Tandem Queueing System) Suppose a service facility consists of two stations in series (tandem), each with its own FIFO queue. Each station consists of a queue and a single server. A customer completing service at station 1 proceeds to station 2, while a customer completing service at station 2 leaves the facility. Assume that the inter-arrival times of customers to station 1 are IID exponential random variables with a mean of 1 minute. Service times of customers at station 1 are exponential random variables with a mean of 0.7 minute, and at station 2 are exponential random variables with mean 0.9 minute. Develop an model for this system. Run the simulation for exactly 20000 minutes and estimate for each station the expected average delay in queue for the customer, the expected time-average number of customers in queue, and the expected utilization. In addition, estimate the average number of customers in the system and the average time spent in the system.
To model this situation, we need to use two resources, one for each server at the two stations.
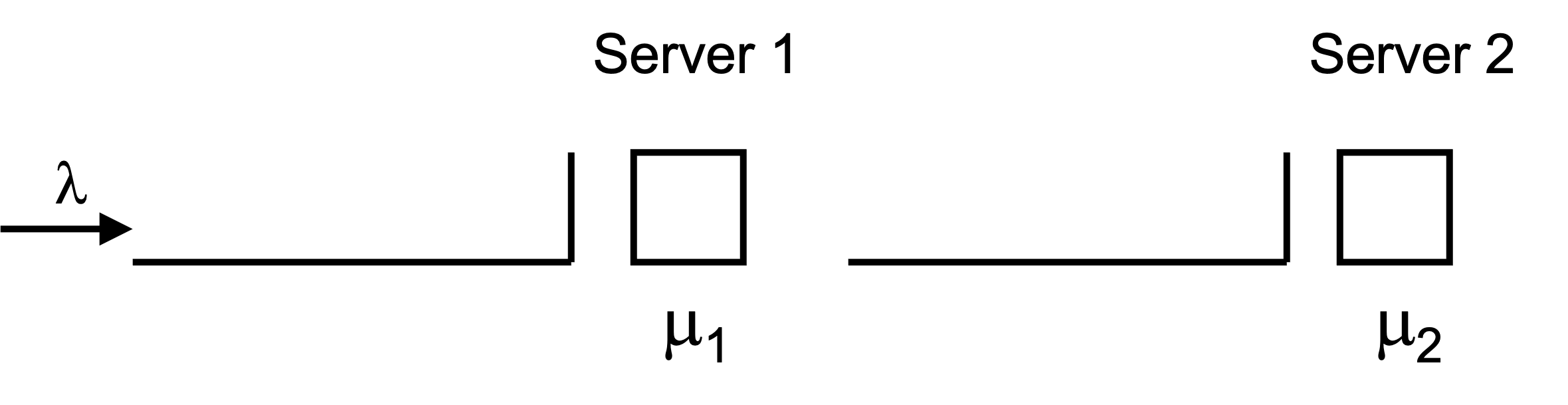
Figure 7.1: Tandem Queue
Figure 7.1 illustrates this situation. This is a perfect application of what we have previously studied about modeling processes. The following code sets up the KSL constructs that are needed within the process modeling.
class TandemQueue(parent: ModelElement, name: String? = null) : ProcessModel(parent, name) {
private val worker1: ResourceWithQ = ResourceWithQ(this, "worker1")
private val worker2: ResourceWithQ = ResourceWithQ(this, "worker2")
private val tba = ExponentialRV(2.0, 1)
private val st1 = RandomVariable(this, ExponentialRV(0.7, 2))
val service1RV: RandomSourceCIfc
get() = st1
private val st2 = RandomVariable(this, ExponentialRV(0.9, 3))
val service2RV: RandomSourceCIfc
get() = st2
private val myArrivalGenerator = EntityGenerator(::Customer, tba, tba)
val generator: EventGeneratorCIfc
get() = myArrivalGenerator
private val wip: TWResponse = TWResponse(this, "${this.name}:NumInSystem")
val numInSystem: TWResponseCIfc
get() = wip
private val timeInSystem: Response = Response(this, "${this.name}:TimeInSystem")
val systemTime: ResponseCIfc
get() = timeInSystemSince the resources will need a queue, we declare the two resources by using the ResourceWithQ class. Then, we specify the random variables that will be used to represent the time between arrivals and the service time at the two stations. Finally, we define the response variables for collecting the number in the system and the time in the system. The process modeling is a straight-forward application of the (seize-delay-release) pattern that was presented in the previous chapter.
private inner class Customer : Entity(){
val tandemQProcess : KSLProcess = process {
wip.increment()
timeStamp = time
seize(worker1)
delay(st1)
release(worker1)
seize(worker2)
delay(st2)
release(worker2)
timeInSystem.value = time - timeStamp
wip.decrement()
}Notice that this code does not save the allocations that are returned by the call to the seize method. This is possible because of two reasons. First, the KSL overloads the release method to allow for the specification of the resource to be released. This overloaded method will release all previously returned allocations that the entity holds of the named resource. Secondly, this situation is a perfect use case for this, because the entity only has seized the worker once before the specified release. Thus, we are simply releasing the last allocation held by the entity via the release() function. It really is user preference whether to save the allocation and then release the allocation or to use the approach of specifying the name of the resource. Of course, this works because releasing all previous allocations is the same as releasing the last one in this situation. In fact, this situation is so common that the KSL provides an additional short cut as illustrated in the following code.
private inner class Customer : Entity(){
val tandemQProcess : KSLProcess = process {
wip.increment()
timeStamp = time
use(worker1, delayDuration = st1)
use(worker2, delayDuration = st2)
timeInSystem.value = time - timeStamp
wip.decrement()
}
}The use method combines the (seize-delay-release) pattern into one method call. The results are not very remarkable.
| Name | Count | Average | Half-Width |
|---|---|---|---|
| worker1:InstantaneousUtil | 30 | 0.351 | 0.002 |
| worker1:NumBusyUnits | 30 | 0.351 | 0.002 |
| worker1:ScheduledUtil | 30 | 0.351 | 0.002 |
| worker1:WIP | 30 | 0.54 | 0.007 |
| worker1:Q:NumInQ | 30 | 0.189 | 0.005 |
| worker1:Q:TimeInQ | 30 | 0.379 | 0.008 |
| worker2:InstantaneousUtil | 30 | 0.45 | 0.003 |
| worker2:NumBusyUnits | 30 | 0.45 | 0.003 |
| worker2:ScheduledUtil | 30 | 0.45 | 0.003 |
| worker2:WIP | 30 | 0.82 | 0.01 |
| worker2:Q:NumInQ | 30 | 0.37 | 0.008 |
| worker2:Q:TimeInQ | 30 | 0.741 | 0.014 |
| TandemQModel:NumInSystem | 30 | 1.36 | 0.014 |
| TandemQModel:TimeInSystem | 30 | 2.723 | 0.02 |
| worker1:SeizeCount | 30 | 7492.333 | 32.526 |
| worker2:SeizeCount | 30 | 7492.533 | 32.356 |
Now we are ready to study the situation of modeling finite space between the two stations.
Example 7.2 (Tandem Queueing System With Blocking) Imagine that at the first station there is a chair for the customer to sit in while receiving service from the first worker. Any customers that arrive while a customer is receiving service at the first station must wait for the server to be free (i.e. the chair to be available). We assume that there is (at least conceptually) an infinite amount of space for the waiting customers at the first station. Now, at the second station, there are two chairs. The customer arriving to the second station will sit in the first chair when receiving service from the server. The second chair is provided for one waiting customer and there is no space for any other customers to wait at the second station. Thus, a customer finishing service at the first station cannot move into (use) the second station if there is a customer waiting at the second station. If a customer at the first station cannot move into the waiting line (2nd chair) at the second station, then the customer is considered blocked. What does this customer do? Well, they are selfish and do not give up their current chair until they can get a chair at the second station. Thus, waiting at the second station may cause waiting to occur at the first station. This situation is called a tandem queue with blocking, as illustrated in Figure 7.2.
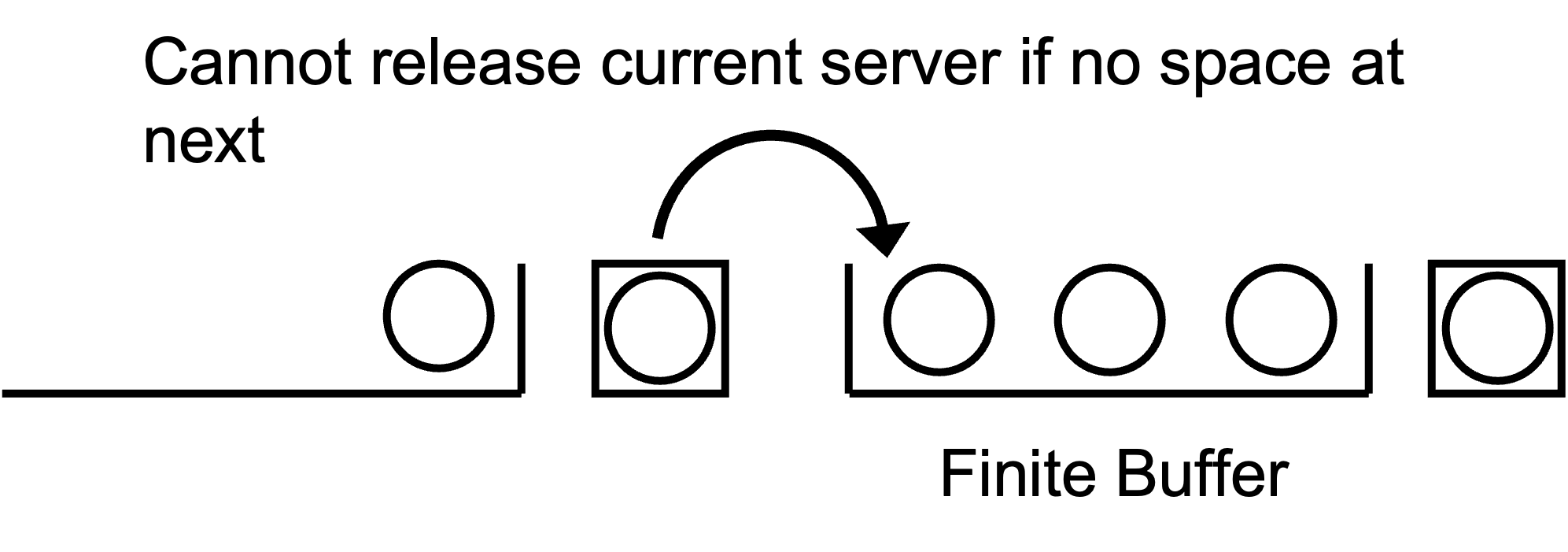
Figure 7.2: Tandem Queue with Blocking
Let’s see how to model this situation using KSL constructs. The key is to model the chair that represents the waiting line at the second station with a resource. This is essentially modeling the waiting space with a resource. In the above scenario, there was one space for waiting.
class TandemQueueWithBlocking(parent: ModelElement, name: String? = null) : ProcessModel(parent, name) {
private val buffer: ResourceWithQ = ResourceWithQ(this, "buffer", capacity = 1)
private val worker1: ResourceWithQ = ResourceWithQ(this, "worker1")
private val worker2: ResourceWithQ = ResourceWithQ(this, "worker2")In this code, we defined a resource called buffer with capacity 1 to represent the chair designated for waiting. By changing the capacity of this resource, we can study the effect of the limited space at the second station on system performance.
Exploring the effect of the buffer size is left as an exercise for the reader. The process modeling needs to be adjusted to account for this space. In the following code, notice the overlapping nature of the seize and release statements.
private inner class Customer : Entity() {
val tandemQProcess: KSLProcess = process {
wip.increment()
timeStamp = time
val a1 = seize(worker1)
delay(st1)
val b = seize(buffer)
release(a1)
val a2 = seize(worker2)
release(b)
delay(st2)
release(a2)
timeInSystem.value = time - timeStamp
wip.decrement()
}
}After receiving service at the first station, the customer attempts to seize the buffer (chair for waiting) at the second station. If there is space in the buffer, then the customer releases the first worker. Don’t give up your chair until you get the next chair! After moving into the chair (buffer), the customer attempts to seize the second worker. If the second worker is not available the customer waits; otherwise, the customer delays for service at the second station, releases the second worker, and then departs that system. Again the key is to have this overlapping seize and release statements.
Figure 7.3 provides the activity diagram for this situation. Notice how the arrows for the seize and release of the resources overlap.
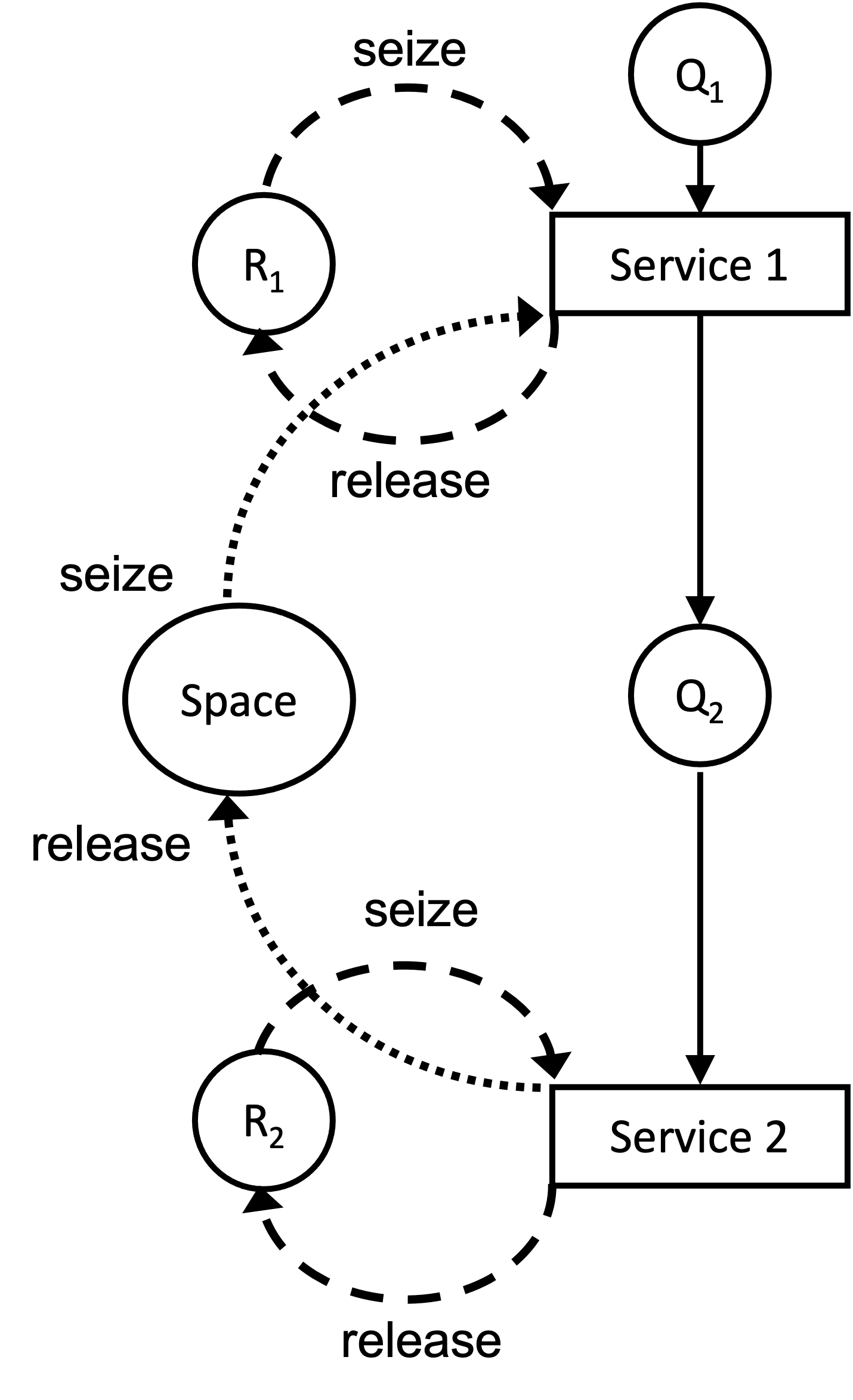
Figure 7.3: Activity Diagram Tandem Queue with Blocking
For the given arrival rate and service parameters, the results indicate that the effect of blocking is not too significant.
| Name | Count | Average | Half-Width |
|---|---|---|---|
| buffer:InstantaneousUtil | 30 | 0.196 | 0.003 |
| buffer:NumBusyUnits | 30 | 0.196 | 0.003 |
| buffer:ScheduledUtil | 30 | 0.196 | 0.003 |
| buffer:WIP | 30 | 0.267 | 0.004 |
| buffer:Q:NumInQ | 30 | 0.071 | 0.002 |
| buffer:Q:TimeInQ | 30 | 0.143 | 0.003 |
| worker1:InstantaneousUtil | 30 | 0.422 | 0.003 |
| worker1:NumBusyUnits | 30 | 0.422 | 0.003 |
| worker1:ScheduledUtil | 30 | 0.422 | 0.003 |
| worker1:WIP | 30 | 0.761 | 0.012 |
| worker1:Q:NumInQ | 30 | 0.339 | 0.009 |
| worker1:Q:TimeInQ | 30 | 0.678 | 0.016 |
| worker2:InstantaneousUtil | 30 | 0.45 | 0.003 |
| worker2:NumBusyUnits | 30 | 0.45 | 0.003 |
| worker2:ScheduledUtil | 30 | 0.45 | 0.003 |
| worker2:WIP | 30 | 0.646 | 0.005 |
| worker2:Q:NumInQ | 30 | 0.196 | 0.003 |
| worker2:Q:TimeInQ | 30 | 0.392 | 0.004 |
| TandemQModelWithBlocking:NumInSystem | 30 | 1.406 | 0.016 |
| TandemQModelWithBlocking:TimeInSystem | 30 | 2.815 | 0.023 |
| buffer:SeizeCount | 30 | 7492.467 | 32.384 |
| worker1:SeizeCount | 30 | 7492.333 | 32.406 |
| worker2:SeizeCount | 30 | 7492.5 | 32.367 |
However, the exercises ask the reader to explore what happens if the arrival rate is increased. A tandem queueing system is just a series of stations. The concept of having stations where work is performed is very useful. A later section illustrates how to generalize these ideas, but first we explore how to organize resources into sets or pools from which resources can be selected.
7.1.2 Resource Pools
A resource pool is a generalization of the concept of a resource that permits individual instances of the Resource class to be combined together into a larger pool of units. Resource pools facilitate the sharing of instances of resources across processes. The important concepts involved in using resource pools are 1) how to select resources to satisfy a request, and 2) how to allocate a request for units across the pool of resources. For example, if a request for units of the pool was for 2 units, and the pool contained 3 individual resources all of capacity 1, which of the 3 resources should be selected to provide the requested units? Also, suppose, for example, the request was for 2 units, and there were 3 individual resources with capacity (1, 2, 3) units, respectively. Should the resource with capacity 2 be used? Should the resource with capacity 3 be used? Should the resource with capacity 1 be used in combination with one of the other resources? As you can see, there may be many possible ways to allocate units to requests when there is a pool of resources. The KSL provides a structure for users to supply selection and allocation rules when using pools of resources through some interfaces.
/**
* Provides for a method to select resources from a list such that
* the returned list may contain resources that can fill the amount needed
*/
fun interface ResourceSelectionRuleIfc {
/**
* @param amountNeeded the amount needed from resources
* @param list of resources to consider selecting from
* @return the selected list of resources. It may be empty
*/
fun selectResources(amountNeeded: Int, list: List<Resource>): List<Resource>
}
/**
* Function to determine how to allocate requirement for units across
* a list of resources that have sufficient available units to meet
* the amount needed.
*/
fun interface AllocationRuleIfc {
/** The method assumes that the provided list of resources has
* enough units available to satisfy the needs of the request.
*
* @param amountNeeded the amount needed from resources
* @param resourceList list of resources to be allocated from
* @return the amount to allocate from each resource as a map
*/
fun makeAllocations(amountNeeded: Int, resourceList: List<Resource>): Map<Resource, Int>
}These two interfaces can be used in combination to form various selection and allocation possibilities for a variety of resource pool situations. The ResourcePool and ResourcePoolWithQ classes use default implementations of these functions. The KSL provides two implementations of the ResourceSelectionRuleIfc interface.
FirstFullyAvailableResourceselects the first resource from a supplied list that can fully meet the request.ResourceSelectionRuleselects a list of resources that (in total) have enough available units to fully meet the request.
It is important to note that the ResourceSelectionRuleIfc interface may return an empty list if the request cannot be met. This is used to determine if the entity must wait.
The KSL provides a default instance of the AllocationRuleIfc interface called DefaultAllocationRule. This rule takes in a list of resources that in total has enough units available and allocates from each listed resource (in the order listed) until the entire amount requested is filled. Thus, in both the selection rule and the allocation rule, the order of the resources within the pool are important. Again, if you want or need to have different rules, then you can implement these interfaces and supply your instances to the ResourcePool and ResourcePoolWithQ classes to use instead of the default implementations. Let’s take a look at an example situation involving resource pools.
Example 7.3 (Resource Pools) In this example, there are two pools. The first pool will have 3 resources (john, paul, and george) and the second pool will have 2 resources (ringo and george). One of the resources (george) is shared (in common) between the two pools. The following code creates the four resources, adds them to lists, and then supplies the lists to instances of the ResourcePoolWithQ class.
class ResourcePoolExample(parent: ModelElement) : ProcessModel(parent, null) {
private val john = Resource(this, name = "John")
private val paul = Resource(this, name = "Paul")
private val george = Resource(this, name = "George")
private val ringo = Resource(this, name = "Ringo")
private val list1 = listOf(john, paul, george)
private val list2 = listOf(ringo, george)
private val pool1: ResourcePoolWithQ = ResourcePoolWithQ(this, list1, name = "pool1")
private val pool2: ResourcePoolWithQ = ResourcePoolWithQ(this, list2, name = "pool2")
private val tba = RandomVariable(this, ExponentialRV(1.0, 1), "Arrival RV")
private val st = RandomVariable(this, ExponentialRV(3.0, 2), "Service RV")
private val decideProcess = RandomVariable(this, BernoulliRV(0.7, 3))
private val wip1 = TWResponse(this, "${name}:WIP1")
private val tip1 = Response(this, "${name}:TimeInSystem1")
private val wip2 = TWResponse(this, "${name}:WIP2")
private val tip2 = Response(this, "${name}:TimeInSystem2")
private val generator = EventGenerator(this, this::arrivals, tba, tba)The two pools are shared between two processes using straightforward (seize-delay-release) logic.
private inner class Customer: Entity() {
val usePool1: KSLProcess = process("Pool 1 Process") {
wip1.increment()
timeStamp = time
val a = seize(pool1, 1)
delay(st)
release(a)
tip1.value = time - timeStamp
wip1.decrement()
}
val usePool2: KSLProcess = process("Pool 2 Process") {
wip2.increment()
timeStamp = time
val a = seize(pool2, 1)
delay(st)
release(a)
tip2.value = time - timeStamp
wip2.decrement()
}
}In this example, we randomly activate the two processes based on a distribution.
private fun arrivals(generator: EventGenerator){
val c = Customer()
if (decideProcess.value.toBoolean()){
activate(c.usePool1)
} else {
activate(c.usePool2)
}
}Since there are four resources and two pools, the performance reports on all the individual resources usage as well as the overall performance of the pool.
Resource Pool Example Statistical Summary Report
| Name | Count | Average | Half-Width |
|---|---|---|---|
| John:InstantaneousUtil | 30 | 0.663 | 0.003 |
| John:NumBusyUnits | 30 | 0.663 | 0.003 |
| John:ScheduledUtil | 30 | 0.663 | 0.003 |
| Paul:InstantaneousUtil | 30 | 0.663 | 0.003 |
| Paul:NumBusyUnits | 30 | 0.663 | 0.003 |
| Paul:ScheduledUtil | 30 | 0.663 | 0.003 |
| George:InstantaneousUtil | 30 | 0.834 | 0.003 |
| George:NumBusyUnits | 30 | 0.834 | 0.003 |
| George:ScheduledUtil | 30 | 0.834 | 0.003 |
| Ringo:InstantaneousUtil | 30 | 0.833 | 0.003 |
| Ringo:NumBusyUnits | 30 | 0.833 | 0.003 |
| Ringo:ScheduledUtil | 30 | 0.833 | 0.003 |
| pool1:NumBusy | 30 | 2.16 | 0.007 |
| pool1:FractionBusy | 30 | 0.72 | 0.002 |
| pool1:Q:NumInQ | 30 | 0.851 | 0.023 |
| pool1:Q:TimeInQ | 30 | 1.708 | 0.044 |
| pool2:NumBusy | 30 | 1.666 | 0.007 |
| pool2:FractionBusy | 30 | 0.833 | 0.003 |
| pool2:Q:NumInQ | 30 | 2.631 | 0.101 |
| pool2:Q:TimeInQ | 30 | 5.253 | 0.193 |
| ResourcePoolExample_3:WIP1 | 30 | 2.34 | 0.028 |
| ResourcePoolExample_3:TimeInSystem1 | 30 | 4.698 | 0.05 |
| ResourcePoolExample_3:WIP2 | 30 | 4.134 | 0.108 |
| ResourcePoolExample_3:TimeInSystem2 | 30 | 8.255 | 0.201 |
| John:SeizeCount | 30 | 3318.533 | 19.247 |
| Paul:SeizeCount | 30 | 3335.833 | 24.126 |
| George:SeizeCount | 30 | 4174.967 | 24.294 |
| Ringo:SeizeCount | 30 | 4151.9 | 23.655 |
Resource pools can be helpful when modeling the sharing of resources between activities. In the next section, we discuss a more complex situation involving a flow shop.
7.1.3 Computer Test and Repair Shop Example
This section presents a common modeling situation in which entities follow a processing plan until they are completed. The KSL makes this type of modeling easy because it can leverage the full functionality of the Kotlin language.
Example 7.4 (Computer Test and Repair Shop) Consider a test and repair shop for computer parts (e.g. circuit boards, hard drives, etc.) The system consists of an initial diagnostic station through which all newly arriving parts must be processed. Currently, newly arriving parts arrive according to a Poisson arrival process with a mean rate of 3 per hour. The diagnostic station consists of 2 diagnostic machines that are fed the arriving parts from a single queue. Data indicates that the diagnostic time is quite variable and follows an exponential distribution with a mean of 30 minutes. Based on the results of the diagnostics, a testing plan is formulated for the parts. There are currently three testing stations 1. 2, 3 which consist of one machine each. The testing plan consists of an ordered sequence of testing stations that must be visited by the part prior to proceeding to a repair station. Because the diagnosis often involves similar problems, there are common sequences that occur for the parts. The company collected extensive data on the visit sequences for the parts and found that the sequences in Table 7.1 constituted the vast majority of test plans for the parts.
| Test Plan | % of Parts | Sequence |
|---|---|---|
| 1 | 25% | 2,3,2,1 |
| 2 | 12.5% | 3,1 |
| 3 | 37.5% | 1,3,1 |
| 4 | 25% | 2,3 |
For example, 25% of the newly arriving parts follow test plan 1, which consists of visiting test stations 2, 3, 2, and 1 prior to proceeding to the repair station.
The testing of the parts at each station takes time that may depend upon the sequence that the part follows. That is, while parts that follow test plan’s 1 and 3 both visit test station 1, data shows that the time spent processing at the station is not necessarily the same. Data on the testing times indicate that the distribution is well modeled with a lognormal distribution with mean, \(\ \mu\), and standard deviation, \(\sigma\) in minutes. Table 7.2 presents the mean and standard deviation for each of the testing time distributions for each station in the test plan.
| Test Plan | Testing Time Parameters | Repair Time Parameters |
|---|---|---|
| 1 | (20,4.1), (12,4.2), (18,4.3), (16,4.0) | (30,60,80) |
| 2 | (12,4), (15,4) | (45,55,70) |
| 3 | (18,4.2), (14,4.4), (12,4.3) | (30,40,60) |
| 4 | (24,4), (30,4) | (35,65,75) |
For example, the first pair of parameters, (20, 4.1), for test plan 1 indicates that the testing time at test station 2 has a lognormal distribution with mean,\(\mu = 20\), and standard deviation,\(\sigma = 4.1\) minutes.
The repair station has 3 workers that attempt to complete the repairs based on the tests. The repair time also depends on the test plan that the part has been following. Data indicates that the repair time can be characterized by a triangular distribution with the minimum, mode, and maximum as specified in the previous table. After the repairs, the parts leave the system. When the parts move between stations assume that there is always a worker available and that the transfer time takes between 2 to 4 minutes uniformly distributed. Figure 7.4 illustrates the arrangement of the stations and the flow of the parts following Plan 2 in the test and repair shop.
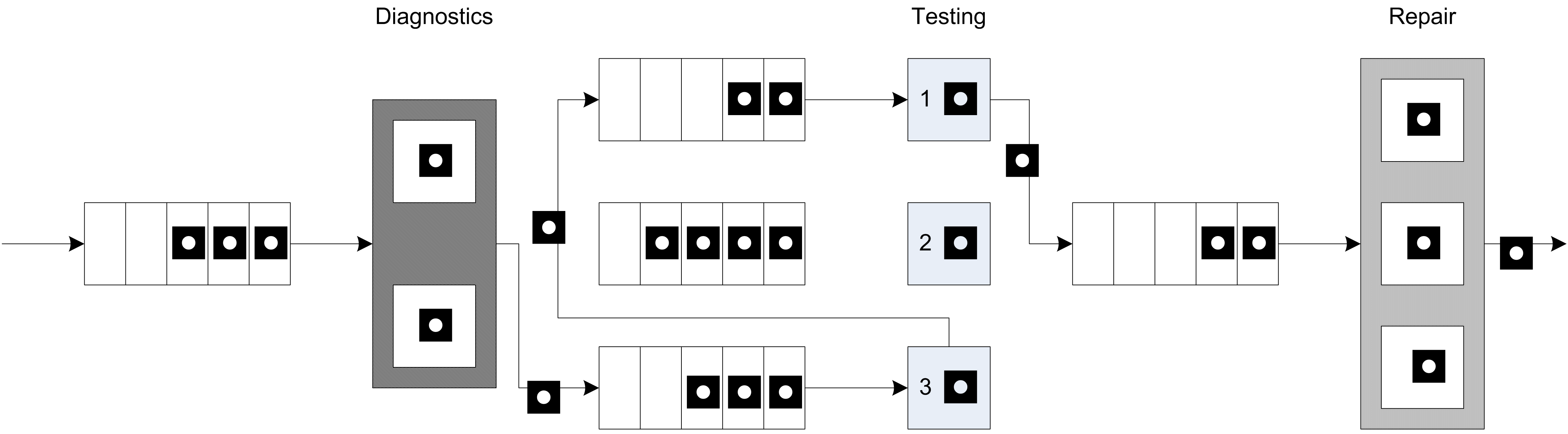
Figure 7.4: Overview of the test and repair shop
The company is considering accepting a new contract that will increase the overall arrival rate of jobs to the system by 10%. They are interested in understanding where the potential bottlenecks are in the system and in developing alternatives to mitigate those bottlenecks so that they can still handle the contract. The new contract stipulates that 80% of the time the testing and repairs should be completed within 480 minutes. The company runs 2 shifts each day for each 5 day work week. Any jobs not completed at the end of the second shift are carried over to first shift of the next working day. Assume that the contract is going to last for 1 year (52 weeks). Build a simulation model that can assist the company in assessing the risks associated with the new contract.
7.1.3.1 Implementing the Test and Repair Model
Before implementing the model, you should prepare by conceptualizing the process flow. Figure 7.5 illustrates the activity diagram for the test and repair system. Parts are created and flow first to the diagnostic station where they seize a diagnostic machine while the diagnostic activity occurs. Then, the test plan is assigned. The flow for the visitation of the parts to the test station is shown with a loop back to the transfer time between the stations. It should be clear that the activity diagram is representing any of the three test stations. After the final test station in the test plan has been visited, the part goes to the repair station, where 1 of 3 repair workers is seized for the repair activity. After the repair activity, the part leaves the system.
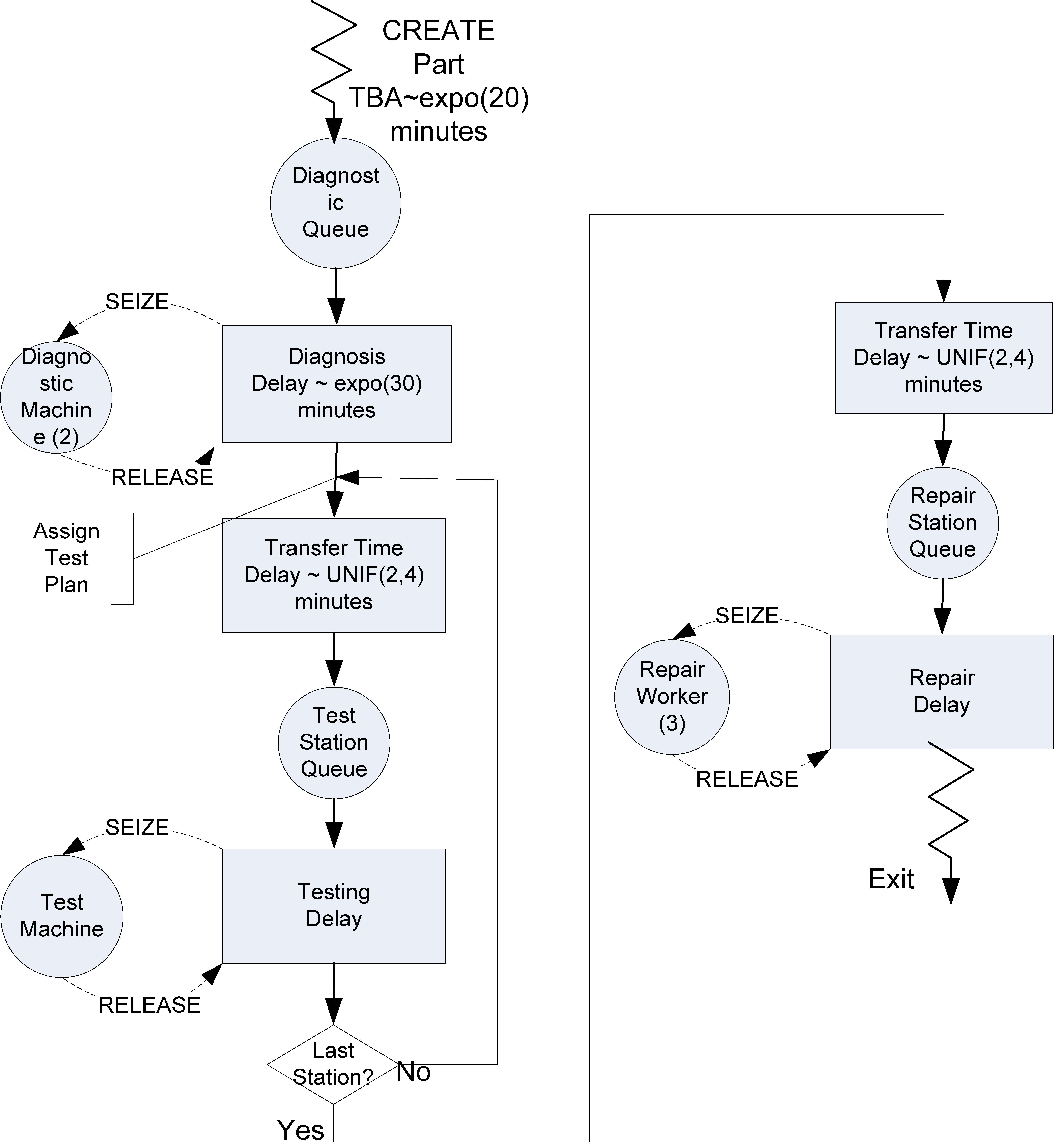
Figure 7.5: Activity diagram for test and repair system
In many modeling contexts, entities will follow a specific path through the system. In a manufacturing job shop, this is often called the process plan. In a bus system, this is called a bus route. In the test and repair system, this is referred to as the test plan. To model a specify path through the system, we need an approach to specify a sequence of stations. A sequence consists of an ordered list of steps. Each step must indicate the resources and other information associated with the step. Thus, a sequence is built by simply providing the list of steps that must be visited. We will use Kotlin lists to hold this information. Let’s take a look at the implementation.
Because of the requirement that different parts follow different sequences and have different processing times based on what resource they are using and where they are in the sequence, there are many random variables that need to be defined for this model.
class TestAndRepairShop(parent: ModelElement, name: String? = null) : ProcessModel(parent, name) {
// define the random variables
private val tba = ExponentialRV(20.0)
private val t11 = RandomVariable(this, LognormalRV(20.0, 4.1))
private val t21 = RandomVariable(this, LognormalRV(12.0, 4.2))
private val t31 = RandomVariable(this, LognormalRV(18.0, 4.3))
private val t41 = RandomVariable(this, LognormalRV(16.0, 4.0))
private val t12 = RandomVariable(this, LognormalRV(12.0, 4.0))
private val t22 = RandomVariable(this, LognormalRV(15.0, 4.0))
private val t13 = RandomVariable(this, LognormalRV(18.0, 4.2))
private val t23 = RandomVariable(this, LognormalRV(14.0, 4.4))
private val t33 = RandomVariable(this, LognormalRV(12.0, 4.3))
private val t14 = RandomVariable(this, LognormalRV(24.0, 4.0))
private val t24 = RandomVariable(this, LognormalRV(30.0, 4.0))
private val r1 = RandomVariable(this, TriangularRV(30.0, 60.0, 80.0))
private val r2 = RandomVariable(this, TriangularRV(45.0, 55.0, 70.0))
private val r3 = RandomVariable(this, TriangularRV(30.0, 40.0, 60.0))
private val r4 = RandomVariable(this, TriangularRV(35.0, 65.0, 75.0))
private val diagnosticTime = RandomVariable(this, ExponentialRV(30.0))
private val moveTime = RandomVariable(this, UniformRV(2.0, 4.0))The code uses a naming convention to keep track of which random variable is using on which sequence. For example, t21 is the random variable required for the second step of the first test plan and r1 is the repair time random variable for the first test plan. For each step of the test plan, we need to know the required resource and the processing time. Thus, we define each of the resources as follows.
// define the resources
private val myDiagnostics: ResourceWithQ = ResourceWithQ(this, "Diagnostics", capacity = 2)
private val myTest1: ResourceWithQ = ResourceWithQ(this, "Test1")
private val myTest2: ResourceWithQ = ResourceWithQ(this, "Test2")
private val myTest3: ResourceWithQ = ResourceWithQ(this, "Test3")
private val myRepair: ResourceWithQ = ResourceWithQ(this, "Repair", capacity = 3)Then, we define a class to hold the information for each step and the lists to represent each of the test plans.
inner class TestPlanStep(val resource: ResourceWithQ, val processTime: RandomIfc)
// make all the plans
private val testPlan1 = listOf(
TestPlanStep(myTest2, t11), TestPlanStep(myTest3, t21),
TestPlanStep(myTest2, t31), TestPlanStep(myTest1, t41), TestPlanStep(myRepair, r1)
)
private val testPlan2 = listOf(
TestPlanStep(myTest3, t12),
TestPlanStep(myTest1, t22), TestPlanStep(myRepair, r2)
)
private val testPlan3 = listOf(
TestPlanStep(myTest1, t13), TestPlanStep(myTest3, t23),
TestPlanStep(myTest1, t33), TestPlanStep(myRepair, r3)
)
private val testPlan4 = listOf(
TestPlanStep(myTest2, t14),
TestPlanStep(myTest3, t24), TestPlanStep(myRepair, r4)
)Now that the test plans are defined, we can develop a method for determining which plan is assigned to each part. The situation description provides a distribution associated with the test plans as provided in Table 7.2. We can use a random list (REmpiricalList) to model this situation.
// set up the sequences and the random selection of the plan
private val sequences = listOf(testPlan1, testPlan2, testPlan3, testPlan4)
private val planCDf = doubleArrayOf(0.25, 0.375, 0.7, 1.0)
private val planList = REmpiricalList<List<TestPlanStep>>(this, sequences, planCDf)The test plans, which are lists, are added to another list called sequences, which will be used from which to randomly select the test plan according to the discrete empirical distribution as provided by the CDF across the test plans.
To capture the performance of the system, we can use Response and TWResponse instances.
private val wip: TWResponse = TWResponse(this, "${this.name}:NumInSystem")
val numInSystem: TWResponseCIfc
get() = wip
private val timeInSystem: Response = Response(this, "${this.name}:TimeInSystem")
val systemTime: ResponseCIfc
get() = timeInSystem
private val myContractLimit: IndicatorResponse = IndicatorResponse({ x -> x <= 480.0 }, timeInSystem, "ProbWithinLimit")
val probWithinLimit: ResponseCIfc
get() = myContractLimitNotice the use of an IndicatorResponse to capture the probability of completing the job within the contract limit. Finally, we can specify the process description for this situation.
private inner class Part : Entity() {
val testAndRepairProcess: KSLProcess = process {
wip.increment()
timeStamp = time
//every part goes to diagnostics
use(myDiagnostics, delayDuration = diagnosticTime)
// determine the test plan
val plan: List<TestPlanStep> = planList.element
// get the iterator
val itr = plan.iterator()
// iterate through the plan
while (itr.hasNext()) {
val tp = itr.next()
use(tp.resource, delayDuration = tp.processTime)
if (tp.resource != myRepair) {
delay(moveTime)
}
}
timeInSystem.value = time - timeStamp
wip.decrement()
}
}Notice how the KSL process constructs and the Kotlin language combine to implement a fairly complex situation within a short and compact process description. The critical item to note is the use of an instance of an iterator within the process. The variable plan is actually randomly generated using the planList discrete empirical list. Then, an iterator for this list is retrieved. The iterator is then used to march through the steps of the assigned test plan within a while loop. Notice that we check if we are not at the repair machine. If we are not, we incur the delay to move to the next machine in the test plan. The process also includes the code to collect statistics on the part as it moves through the process. To setup to execute this code, we specify the run length and the number of replications.
fun main() {
val m = Model()
val tq = TestAndRepairShop(m, name = "TestAndRepair")
m.numberOfReplications = 10
m.lengthOfReplication = 52.0* 5.0*2.0*480.0
m.simulate()
m.print()
val r = m.simulationReporter
r.writeHalfWidthSummaryReportAsMarkDown(KSL.out, df = MarkDown.D3FORMAT)
}The output is quite lengthy so the code captures it as a Markdown table.
| Name | Count | Average | Half-Width |
|---|---|---|---|
| Diagnostics:InstantaneousUtil | 10 | 0.744 | 0.007 |
| Diagnostics:NumBusyUnits | 10 | 1.489 | 0.013 |
| Diagnostics:ScheduledUtil | 10 | 0.744 | 0.007 |
| Diagnostics:WIP | 10 | 3.332 | 0.123 |
| Diagnostics:Q:NumInQ | 10 | 1.844 | 0.11 |
| Diagnostics:Q:TimeInQ | 10 | 36.964 | 2.043 |
| Test1:InstantaneousUtil | 10 | 0.855 | 0.005 |
| Test1:NumBusyUnits | 10 | 0.855 | 0.005 |
| Test1:ScheduledUtil | 10 | 0.855 | 0.005 |
| Test1:WIP | 10 | 4.1 | 0.283 |
| Test1:Q:NumInQ | 10 | 3.245 | 0.279 |
| Test1:Q:TimeInQ | 10 | 57.692 | 4.736 |
| Test2:InstantaneousUtil | 10 | 0.773 | 0.006 |
| Test2:NumBusyUnits | 10 | 0.773 | 0.006 |
| Test2:ScheduledUtil | 10 | 0.773 | 0.006 |
| Test2:WIP | 10 | 2.319 | 0.132 |
| Test2:Q:NumInQ | 10 | 1.546 | 0.126 |
| Test2:Q:TimeInQ | 10 | 41.279 | 3.062 |
| Test3:InstantaneousUtil | 10 | 0.858 | 0.006 |
| Test3:NumBusyUnits | 10 | 0.858 | 0.006 |
| Test3:ScheduledUtil | 10 | 0.858 | 0.006 |
| Test3:WIP | 10 | 3.417 | 0.273 |
| Test3:Q:NumInQ | 10 | 2.559 | 0.269 |
| Test3:Q:TimeInQ | 10 | 51.318 | 5.176 |
| Repair:InstantaneousUtil | 10 | 0.864 | 0.006 |
| Repair:NumBusyUnits | 10 | 2.591 | 0.017 |
| Repair:ScheduledUtil | 10 | 0.864 | 0.006 |
| Repair:WIP | 10 | 3.824 | 0.135 |
| Repair:Q:NumInQ | 10 | 1.233 | 0.12 |
| Repair:Q:TimeInQ | 10 | 24.733 | 2.273 |
| TestAndRepair:NumInSystem | 10 | 17.572 | 0.803 |
| TestAndRepair:TimeInSystem | 10 | 352.487 | 14.262 |
| ProbWithinLimit | 10 | 0.817 | 0.028 |
| Diagnostics:SeizeCount | 10 | 12443.4 | 75.921 |
| Test1:SeizeCount | 10 | 14027 | 76.189 |
| Test2:SeizeCount | 10 | 9337.3 | 77.976 |
| Test3:SeizeCount | 10 | 12436.4 | 76.419 |
| Repair:SeizeCount | 10 | 12430.7 | 75.528 |
It looks like test machine 3 and the repair station have the highest estimated utilization values. An increase in the amount of work to the test and repair shop may have issues at those stations. The reader is asked to explore the performance of this situation in the exercises.
In the next section, we examine an even more complex situation involving systems that have parameters or distributions that depend on time.