2.4 Distribution Fitting Using the KSL
This section describes how to apply the methods discussed in Appendix B to fit probability distributions using the KSL. The package ksl.utilities.distributions.fitting contains classes that facilitate the estimation of the parameters of discrete and continuous probability distributions. In addition, the quality of the estimated parameters can be examined based on a number of metrics that measure the goodness of fit of the probability model to the data. Finally, there is functionality that will automatically fit a set of possible distributions to a data set and recommend the best distribution based on a combination of metrics. This section will first describe the organization of the functionality related to parameter estimation. Then, the scoring models for measuring the quality of fit will be presented. Finally, a number of examples will illustrate the use of the classes on the data from the examples discussed in Appendix B.
2.4.1 Estimating Distribution Parameters
As discussed in Appendix B a key step in the distribution fitting process is estimating the parameters of the hypothesized probability model. For example, if we want to fit a normal distribution to the data, we must estimate the mean (\(\mu\)) and the variance (\(\sigma^2\)) of the associated distribution. Each distribution may be specified by different parameters. For example, the gamma distribution is specified by the shape (\(\alpha\)) and scale (\(\beta\)) parameters. Appendix E.1 and E.2 provide a listing of many common distributions and their parameters.
The estimation of the parameters of a distribution requires the execution of an algorithm. As mentioned in Appendix B, the maximum likelihood estimation method is commonly used because it often produces estimates that have desirable statistical properties. However, the maximum likelihood method may require the solving of a non-linear optimization problem. The method of moments is also a common algorithm that is used to estimate the parameters of various distributions. In the method of moments, the theoretical moment equations are matched with the statistically computed moments resulting in a set of equations that must be solved to form the parameter estimators. In some cases, the method of moments results in simple equations, but for some distributions it may result in the need to solve a system of non-linear equations. Many other methods of parameter estimation exist, such as the percentile method, which may be general or targeted to specific distributions. The KSL facilitates the development of routines to estimate parameters by providing a well-defined parameter estimation interface. By implementing the ParameterEstimatorIfc interface, KSL users can incorporate additional distributions and estimation methods into the estimation framework.
Figure 2.7: Important Classes for Parameter Estimation
Figure 2.7 illustrates some of the key classes and interfaces involved in the parameter estimation framework. The functionality starts with the ParameterEstimatorIfc interface, which requires the implementation of the estimation routine and a property (checkRange) to indicate if the data should be checked for shifting onto the domain of the distribution. The ParameterEstimatorIfc interface defines a general function that uses 1-dimensional data array, and estimates the parameters of an hypothesized uni-variate distribution via some estimation algorithm. It is important to note that a distribution may have more than one method for estimating its parameters. In the figure, the maximum likelihood estimator for the gamma distribution is illustrated; however, for example, there is also a method of moments estimator for the gamma distribution implemented within the KSL distribution fitting framework.
interface ParameterEstimatorIfc {
/**
* Indicates if the estimator requires that the range of the data be checked for a shift
* before the estimation process.
*/
val checkRange: Boolean
/**
* Estimates the parameters associated with some distribution. The returned [EstimationResult]
* needs to be consistent with the intent of the desired distribution.
* Note the meaning of the fields associated with [EstimationResult]
*/
fun estimateParameters(data: DoubleArray, statistics: StatisticIfc = Statistic(data)): EstimationResult
}The basic contract for the estimation process is that the returned EstimationResult is consistent with the required parameter estimation. The data class EstimationResult stores information about the estimation process to be returned as a result of its application on the supplied data. The key property is the success property, which indicates whether the parameter estimation process was successful. Given that many estimation processes may require advanced optimization methods, the estimation process might not converge or some other problem might have occurred. If the success property is true, then the results should be meaningful. The EstimationResult also returns the estimator that was used (MVBSestimatorIfc) in a form for bootstrapping, the estimated parameters as an instance of RVParameters, a message concerning the estimation process, a text (string) representation of the distribution and its parameters, the original data (originalData), the shifted data if shifted, the statistics associated with the original data, and data that is suitable for testing for goodness of fit (testData). The MVBSestimatorIfc interface defines a method that takes in an array of data and produces an (double) array that holds the estimated parameters. In addition, the interface defines a list of the names to use for the parameters. This form for the estimation results facilitates performing a bootstrapping process that can provide confidence intervals for the estimated parameters.
Example 2.23 (Parameter Estimation) The following code illustrates the estimation of the parameters for a normal distribution.
fun main(){
// define a normal random variable,
val x = NormalRV(2.0, 5.0)
// generate some data
val data = x.sample(100)
// create the estimator
val ne = NormalMLEParameterEstimator
// estimate the parameters
val result = ne.estimateParameters(data)
println(result)
val bss = BootstrapSampler(data, ne)
val list = bss.bootStrapEstimates(400)
for (element in list) {
println(element.toString())
}
}The results of this estimation process are show here. Notice that the estimation process was successful and the summary statistics were reported. The data was not shifted for the estimation process and the estimated parameters were \(\mu = 2.4138851463671918\) and \(\sigma^2 = 5.571943618235626\). The bootstrapping process, see Section 8.1 of Chapter 8 was used to provide confidence intervals on the estimated parameters. This functionality is available for any of the distributions and the estimation routines that have been defined within the KSL.
Estimation Results:
The estimation was a SUCCESS!
Estimation message:
The normal parameters were estimated successfully using a MLE technique
Statistics for the data:
ID 2
Name Statistic_1
Number 100.0
Average 2.4138851463671918
Standard Deviation 2.360496477064862
Standard Error 0.23604964770648623
Half-width 0.4683737087091538
Confidence Level 0.95
Confidence Interval [1.945511437658038, 2.8822588550763455]
Minimum -3.5669763460675563
Maximum 7.965700083130213
Sum 241.38851463671918
Variance 5.571943618235626
Deviation Sum of Squares 551.622418205327
Last value collected 3.241841050111711
Kurtosis -0.5348553870721524
Skewness 0.20030433873223535
Lag 1 Covariance -1.2167682247913674
Lag 1 Correlation -0.2205799084000348
Von Neumann Lag 1 Test Statistic -2.213606239550482
Number of missing observations 0.0
Lead-Digit Rule(1) -1
Shift estimation results:
null
Estimated parameters:
RV Type = Normal
Double Parameters {mean=2.4138851463671918, variance=5.571943618235626}
Integer Parameters {}
Double Array Parameters {}
------------------------------------------------------
Bootstrap statistical results:
------------------------------------------------------
statistic name = mean
number of bootstrap samples = 400
size of original sample = 100
original estimate = 2.4138851463671918
bias estimate = -0.004346113299975141
across bootstrap average = 2.4095390330672166
std. err. estimate = 0.011727975525999638
default c.i. level = 0.95
norm c.i. = [2.3908987367061334, 2.43687155602825]
basic c.i. = [1.9728453671368813, 2.8775812826012266]
percentile c.i. = [1.950189010133157, 2.854924925597502]
------------------------------------------------------
------------------------------------------------------
Bootstrap statistical results:
------------------------------------------------------
statistic name = variance
number of bootstrap samples = 400
size of original sample = 100
original estimate = 5.571943618235626
bias estimate = -0.15846349216845024
across bootstrap average = 5.413480126067176
std. err. estimate = 0.032372344482434104
default c.i. level = 0.95
norm c.i. = [5.508494988903779, 5.635392247567474]
basic c.i. = [4.436576208323049, 7.000150587007805]
percentile c.i. = [4.143736649463448, 6.707311028148204]
------------------------------------------------------The parameters of the following distributions can be estimated from data using the KSL.
- Beta - via
BetaMOMParameterEstimator - Binomial - via
BinomialMaxParameterEstimatororBinomialMOMParameterEstimator - Exponential - via
ExponentialMLEEstimator - Gamma - via
GammaMLEParameterEstimatororGammaMOMParameterEstimator - Generalized Beta - via
GeneralizedBetaMOMParameterEstimator - Laplace - via
LaplaceMLEParameterEstimator - Logistic - via
LogisticMOMParameterEstimator - Lognormal - via
LognormalMLEParameterEstimator - Negative Binomial - via
NegBinomialMOMParameterEstimator - Normal - via
NormalMLEParameterEstimator - Pearson Type 5 - via
PearsonType5MLEParameterEstimator - Poisson - via
PoissonMLEParameterEstimator - Triangular - via
TriangularParameterEstimator - Uniform - via
UniformParameterEstimator - Weibull - via
WeibullMLEParameterEstimatororWeibullPercentileParameterEstimator
Again, by implementing the concepts illustrated in Figure 2.7, a KSL user can implement additional distribution parameter estimation methods. If you need to fit a distribution that is not modeled within the KSL, then you need to implement the distribution’s parameter estimation procedure. In addition, you will also need to implement a class representing the distribution. Depending on the type of distribution, this may involve implementing the requirements of the ContinuousDistributionIfc interface or the DiscreteDistributionIfc interface for the underlying probability model.
2.4.2 Continuous Distribution Recommendation Framework
As described in Appendix B, the distribution modeling process may require that the parameters of many distributions be estimated and the quality of those probability models examined to recommend an overall distribution. This process normally involves statistical tests or metrics (e.g. square error criterion) to assess how well the probability model represents the data.
Rather than relying on statistical tests, the KSL’s distribution recommendation framework defines a set of criteria for assessing the quality of the probability model’s representation. These criteria are called scoring models. Figure 2.8 illustrates the scoring models that the KSL uses within its automated fitting process. To implement your own scoring model, you need to sub-class from the abstract base class PDFScoringModel.
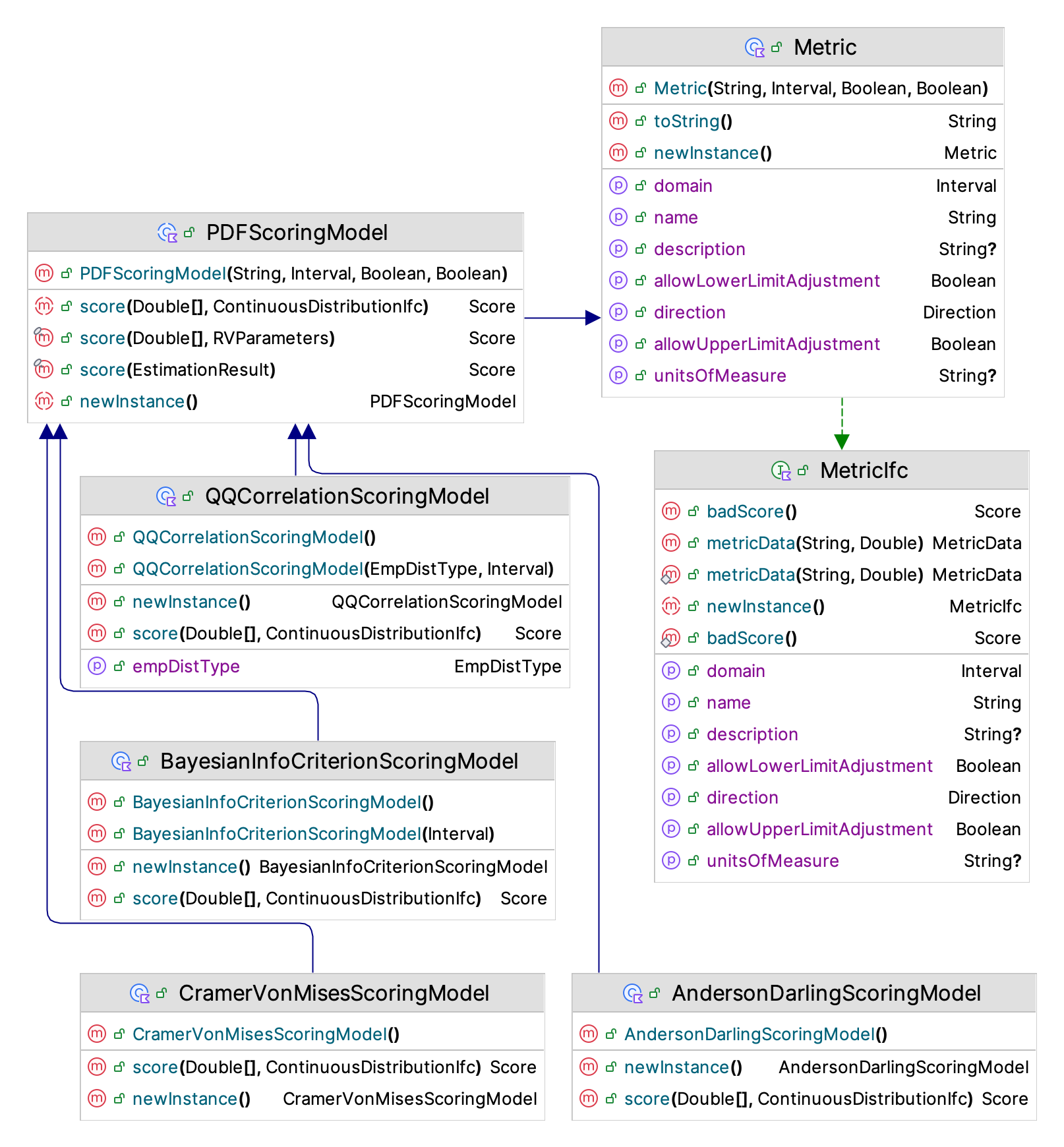
Figure 2.8: Important Classes for PDF Scoring
The primary method that needs to be implemented is the abstract score() function.
The contract for this function is it will return a numerical value that measures the quality of the distribution fit given the observed data and a hypothesized continuous distribution function. In addition, the function, badScore(), should return the worse possible score for the metric. The badScore() function should be used if there is some error or issue that prevents the scoring procedure from determining a score for the fit. A Score is a data class that indicates whether the score is valid or not and provides the metric that determined the score. You can think of the metric as the units of measure. The metric defines the domain (or set of legal values) for the metric and its direction. By direction, we mean whether bigger scores are better than smaller scores or vice versa. This information is used when a set of scores are combined into an overall score.
The KSL has many pre-defined scoring models. The user can specify the criteria to use for the scoring evaluation process or accept the defaults. Two of the scoring models are based on a histogram summary of the data. This involves dividing the range of observations via break points \(b_j\) and tabulating frequencies or proportions of the data falling with the defined intervals or bins. The KSL does not use arbitrary break points from a histogram binning process. Instead the KSL attempts to define the break points for the intervals such that each interval has the same probability of occurrence. This ensures that the expected number of observations within each interval is the same. The theoretical basis for this approach can be found in (Williams 1950).
The scoring criteria based on a binning process are the sum of squared errors (SSE), Chi-Squared (CSQ), and the Mallows L2 (ML2) criterion. For these models, let \(c_{j}\) be the observed count of the \(x\) values contained in the \(j^{th}\) interval \(\left(b_{j-1}, b_{j} \right]\), let \(h_j = c_j/n\) be the relative frequency for the \(j^{th}\) interval, and let \(p_j\) be defined as:
\[ p_j = P\{b_{j-1} \leq X \leq b_{j}\} = \int\limits_{b_{j-1}}^{b_{j}} f(x) \mathrm{d}x \] Thus, we can define SSE, CSQ, and ML2 as follows:
- Sum of Squared Error (SSE) criterion - The squared error is defined as the sum over the intervals of the squared difference between the relative frequency and the theoretical probability associated with each interval:
\[ \text{SSE} = \sum_{j = 1}^k (h_j - p_j)^2 \]
- Chi-Squared criterion (CSQ) - The chi-squared criterion is the \(\chi^{2}\) test statistic value that compares the observed counts \(c_j\) to the expected counts \(np_j\) over the intervals.
\[ \chi^{2}_{0} = \sum\limits_{j=1}^{k} \frac{\left( c_{j} - np_{j} \right)^{2}}{np_{j}} \]
- Mallows L2 Criterion - (Levina and Bickel 2001) provide the definition of the Mallows L2 distance, also known as the earthmovers distance. In terms of \(p_j\) and \(h_j\), this is:
\[ M_{L_2} = \Bigg( \frac{1}{k} \sum_{j=1}^{k}(h_j - p_j)^2\Bigg)^{\frac{1}{2}} \]
Note that under the specification of the breakpoints resulting in intervals with equal probabilities, we have \(p_j = p\) and \(p = k/n\). This allows the SSE criterion to be simplified as follows:
\[ \text{SSE} = \sum_{j = 1}^k (h_j - p_j)^2 = \sum_{j = 1}^k (h_j - p)^2 \]
In addition, the Mallows criterion can be written in terms of the SSE as follows:
\[ M_{L_2} = \Bigg( \frac{1}{k} \sum_{j=1}^{k}(h_j - p_j)^2\Bigg)^{\frac{1}{2}} = \Bigg( \frac{\text{SSE} }{k} \Bigg)^{\frac{1}{2}} \]
Thus, we have \(M^2_{L_2} = \frac{\text{SSE} }{k}\). Finally, notice that the chi-squared criterion (CSQ) under the assumption that \(p_j = p\) can be simplified as:
\[ \chi^{2}_{0} = \sum\limits_{j=1}^{k} \frac{\left( c_{j} - np_{j} \right)^{2}}{np_{j}}= n \sum\limits_{j=1}^{k} \frac{\left( h_{j} - p_{j} \right)^{2}}{p_{j}} = \frac{n}{p}\sum\limits_{j=1}^{k} \left( h_{j} - p \right)^{2} = \frac{n}{p}\text{SSE} \]
Therefore, under the assumption that \(p_j = p\), that is equally probable intervals, we have that:
\[ \chi^{2}_{0} = \frac{n^2}{k}\text{SSE}=n^2M^2_{L_2} \] The relationships between CSQ, SSE, and ML2 are important to note because during the scoring process, the metrics are converted to a common scale. If a linear transformation is chosen for the transformation (which is the default), then the resulting values for CSQ, SSE, and ML2 will be the same in terms of their scaled values. Thus, under a linear transformation, only one of CSQ, SSE, and ML2 should be included in the evaluation process.
The metrics that do not depend on a histogram binning process include the Kolmogorov-Smirnov (KS) criterion, Cramer Von Mises (CVM) criterion, Anderson-Darling (AD) criterion, P-P plot sum of squared errors (PPSSE), P-P plot correlation (PPC), Q-Q plot sum of squared errors (QQSSE), Q-Q plot correlation (QQC), Bayesian Information Criterion (BIC), and the Akaike Information Criterion (AIC). These scoring metrics are defined as follows:
- Kolmogorov-Smirnov criterion - The Kolmogorov-Smirnov (KS) criterion is based on the K-S test statistic, where, \(D_{n} = \max \lbrace D^{+}_{n}, D^{-}_{n} \rbrace\), represents the largest vertical distance between the hypothesized distribution and the empirical distribution over the range of the distribution.
\[ \begin{aligned} D^{+}_{n} & = \underset{1 \leq i \leq n}{\max} \Bigl\lbrace \tilde{F}_{n} \left( x_{(i)} \right) - \hat{F}(x_{(i)}) \Bigr\rbrace \\ & = \underset{1 \leq i \leq n}{\max} \Bigl\lbrace \frac{i}{n} - \hat{F}(x_{(i)}) \Bigr\rbrace \end{aligned} \]
\[ \begin{aligned} D^{-}_{n} & = \underset{1 \leq i \leq n}{\max} \Bigl\lbrace \hat{F}(x_{(i)}) - \tilde{F}_{n} \left( x_{(i-1)} \right) \Bigr\rbrace \\ & = \underset{1 \leq i \leq n}{\max} \Bigl\lbrace \hat{F}(x_{(i)}) - \frac{i-1}{n} \Bigr\rbrace \end{aligned} \]
- Cramer Von Mises criterion (CVM) - The Cramer Von Mises criterion is a distance measure used to compare the goodness of fit of a cumulative distribution function, \(F(x)\) to the empirical distribution, \(F_n(x)\). The distance is defined as:
\[\begin{equation} \omega^2 = \int_{-\infty}^{+\infty}\Big[ F_n(x) - F(x) \Big]^2\,dF(x) \end{equation}\]
The CVM metric can be computed from data sorted in ascending order (\(x_1, x_2, \cdots, x_n\)), i.e. the order statistics, as:
\[\begin{equation} T = n\omega^2 = \frac{1}{12n} + \sum_{i=1}^{n}\Big[ \frac{2i-1}{2n} - F(x_i) \Big]^2 \end{equation}\]
- Anderson Darling criterion (AD) - The Anderson-Darling criterion is similar in spirit to the Cramer Von Mises test statistic except that it is designed to detect discrepancies in the tails of the distribution.
\[\begin{equation} A^2 = n\int_{-\infty}^{+\infty}\frac{\Big[ F_n(x) - F(x) \Big]^2}{F(x)(1-F(x))}\,dF(x) \end{equation}\]
The AD metric can be computed from data sorted in ascending order (\(x_1, x_2, \cdots, x_n\)), i.e. the order statistics, as:
\[\begin{equation} A^2 = -n - \sum_{i=1}^{n}\frac{2i-1}{n}\Big[ \ln(F(x_i)) + \ln(1-F(x_{n+1-i})) \Big] \end{equation}\]
- P-P Plot Sum of Squared Errors (PPSSE) - Based on the concepts found in (Gan and Koehler 1990), the sum of squared error related to the P-P plot of the theoretical distribution versus the empirical distribution was developed as a scoring criterion. Let \((x_{(1)}, x_{(2)}, \ldots x_{(n)})\) be the order statistics. Let the theoretical distribution be represented with \(\hat{F}(x_{(i)})\) for \(i= 1, 2, \ldots n\) where \(\hat{F}\) is the CDF of the hypothesized distribution. Define the empirical distribution as
\[\tilde{F}_n(x_{(i)}) = \dfrac{i - 0.5}{n}\]
Then, the P-P Plot sum of squared error (PPSSE) criterion is defined as:
\[ \text{PP Squared Error} = \sum_{i = 1}^n (\tilde{F}_n(x_{(i)}) - \hat{F}(x_{(i)}))^2 \]
Notice that the Cramer-Von-Mises criterion and the PPSSE criterion are related as follows:
\[ T = \frac{1}{12n} + \text{PPSSE} \]
Therefore, under a linear transformation, it is not recommended to include both PPSSE and CVM in the evaluation process.
P-P Correlation (PPC) - Based on the concepts found in (Gan and Koehler 1990), the P-P correlation scoring model computes the Pearson correlation associated with a P-P plot. That is, the scoring model computes the correlation between \((\tilde{F}_n(x_{(i)}), \hat{F}(x_{(i)}))\) for \(i= 1, 2, \ldots n\).
Q-Q Plot Sum of Squared Error (QQSSE) - Again, based on the concepts found in (Gan and Koehler 1990), the sum of squared error related to the Q-Q plot of the theoretical quantiles versus the empirical quantiles was developed as a scoring criterion. For a Q-Q plot define \(q_i = (i - 0.5)/n\), for \(i= 1, 2, \ldots n\) and \(x_{q_i} = \hat{F}^{-1} (q_i)\) where \(\hat{F}^{-1}(\cdot)\) is the inverse CDF of the hypothesized distribution. Finally, let \((x_{(1}, x_{(2)}, \ldots x_{(n)})\) be the order statistics. Then, the QQSSE is the sum of the squared error as follows:
\[ \text{QQSSE} = \sum_{i = 1}^n (x_{(i)} - x_{q_i})^2 \]
Q-Q Plot Correlation (QQC) - Similar to PPC, the Q-Q plot correlation criterion is the Pearson correlation of \((x_{(i)},x_{q_i})\) for \(i= 1, 2, \ldots n\), with values closer to 1.0 indicating a good fit.
Bayesian Information Criterion (BIC) - Developed by (Schwarz 1978), the BIC is used for model selection where models with lower BIC are preferred. The BIC is based on the log-likelihood function. Let \(f(x;\vec{\theta})\) be the theoretical probability density function with parameters \(\vec{\theta}\). The likelihood function of a sample of \(\vec{x} = (x_1,x_2, \cdots, x_n)\) is:
\[ L(\vec{\theta};\vec{x}) = \prod_{i=1}^{n}f(x_i;\vec{\theta}) \] The likelihood function of the sample, measures the likelihood that the sample came from the distribution with the given parameters. The log-likelihood function for an observation \(x_i\) is \(\ln \big(f(x_i;\vec{\theta}\big)\). Thus, the log-likelihood function for the sample is:
\[ \text{LL}(\vec{\theta};\vec{x}) = \sum_{i=1}^{n}ln(f(x_i;\vec{\theta})) \] The BIC is defined in terms of the value of the log-likelihood of the sample as follows:
\[ \text{BIC} = k\ln(n) - 2\text{LL}(\hat{\vec{\theta}};\vec{x}) \]
where \(n\) is the sample size, \(k\) is the number of parameters estimated for the model, \(\hat{\vec{\theta}}\) are the estimated parameter values.
- Akaike Information Criterion (AIC) - Developed by (Akaike 1974), the AIC is used for model selection where models with lower AIC are preferred. Like the BIC, the AIC is defined in terms of the log-likelihood function of the sample. The KSL uses the formulation described in (Vose 2010) as follows:
\[ \text{AIC} = \Bigg( \frac{n-2k +2}{n-k+1}\Bigg) -2\text{LL}(\hat{\vec{\theta}};\vec{x}) \]
These scoring models avoid summarizing the data based on a histogram, which requires a specification of the bin sizes (or widths) and tabulation of frequencies or proportions associated with the bins.
As illustrated in Figure 2.8, the scoring models are implemented by sub-classing from the PDFScoringModel abstract base class. Users of the KSL distribution recommendation framework can select which scoring models to include during the evaluation process. The default set of scoring models are BIC, AD, CVM, and QQC. During testing, the BIC criterion performed very well across all but very low sample sizes. The AD and CVM criteria tend to perform better for lower sample sizes, while the QQC criterion tends to perform better for higher sample sizes and for particular distribution families.
The quality of a parametric fit for a specific distribution can be evaluated by one or more scoring models. Since distribution quality metrics have been designed to measure different aspects of the fit, the KSL allows the scoring results to be combined into an overall score. Suppose distribution \(F_k\) is evaluated by the the scoring models, each resulting in score \(S_i\) for \(i=1,2,\cdots, m\), where \(m\) is the number of scoring models. In general, the scores may not have the same scales and the same direction of goodness. The KSL scoring system translates and scales each score \(S_i\) in to a value, \(M_i\) measure, that has a common scale and direction (a bigger score is better). These value measures are then combined into an overall value (\(V_k\)) for the distribution using weights (\(w_i\)) across the scoring criteria:
\[\begin{equation} V_{k} = \sum_{i=1}^{m}w_i \times M_i \end{equation}\]
The distribution that has the overall largest value, \(V_k\), is then recommended as the best fitting probability model.
This methodology is based on the commonly used multi-objective decision analysis (MODA) method for choosing among a set of alternatives. In the KSL default application of this methodology, each scoring model is weighted equally and a linearly additive model is assumed. The framework is designed to allow the user to define and apply their own scoring models and to set the preference weights among the metrics. In addition, sensitivity analysis of the weights can easily be accomplished. Once the best distribution has been recommended, then the KSL facilitates performing statistical tests with resulting p-values.
Figure 2.9 presents the main class (PDFModeler) for performing the continuous distribution fitting task. The companion object provides functionality to estimate the shift parameter, shift the data to the left, compute confidence intervals for the minimum and maximum of the data via bootstrapping, estimate the range of possible values for the distribution, create distributions from estimated parameters, create the default evaluation model, and work with histograms.
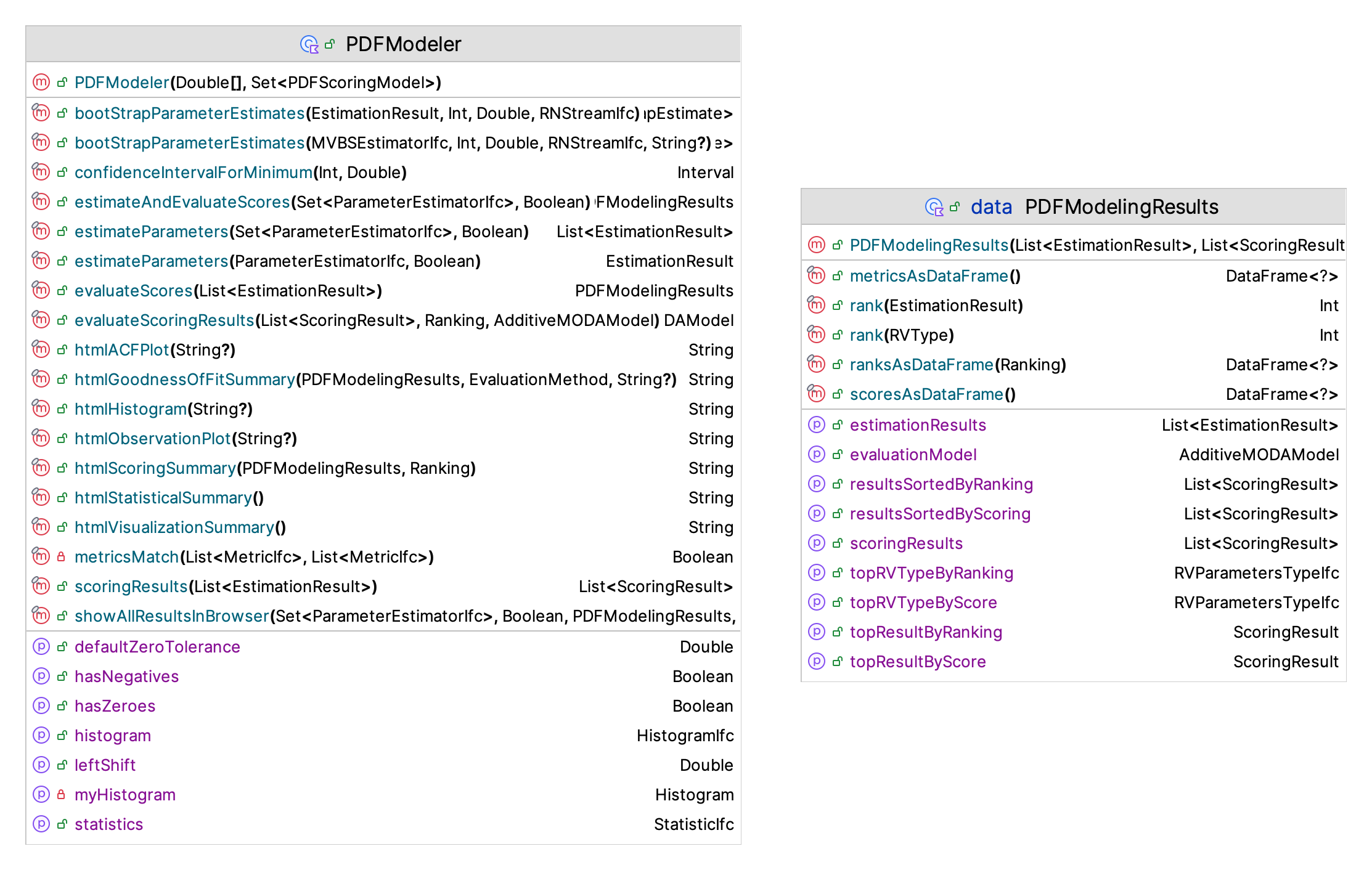
Figure 2.9: PDF Modeling Framework
The modeling process starts with creating an instance of PDFModeler by supplying the data to be modeled and the set of scoring models to be used within the evaluation process. Then, functions can be used to perform the estimation and scoring tasks.
estimateParameters(estimators: Set<ParameterEstimatorIfc>, automaticShifting: Boolean = true)- This function estimates the parameters for all estimators represented by the supplied set of estimators. The parameter,automaticShiftingcontrols whether the data will be automatically shifted. If the automatic shift parameter is true (the default), then a confidence interval for the minimum of the data is estimated from the data. If the upper limit of the estimated confidence interval is greater than the value specified by the default zero tolerance property, then the data is shifted to the left and used in the estimation process. The estimated shift will be recorded in the result. Automated shift estimation will occur only if the automatic shifting parameter is true, if the estimator requires that its range be checked, and if the data actually requires a shift. If the automatic shifting parameter is false, then no shifting will occur. In this case it is up to the user to ensure that the supplied data is representative of the set of estimators to be estimated. The returned list will contain the results for each estimator.evaluateScores(estimationResults: List<EstimationResult>)- This function applies the supplied scoring models to the results from the parameter estimation process. Each distribution with estimated parameters will be scored by each of the supplied models and the results tabulated as an instance of thePDFModelingResultsclass.estimateAndEvaluateScores(estimators: Set<ParameterEstimatorIfc> = allEstimators, automaticShifting: Boolean = true, scoringModels: Set<PDFScoringModel> = allScoringModels)- As its name implies, this function combines the functions ofestimateParameters()andevaluateScores()into a single function for the convenience of the modeler. The returned instance of thePDFModelingResultsclass has the estimation results and the scoring results.showAllResultsInBrowser(fileName: String = "pdfModelingResults")- This function makes a histogram, observations plot, auto-correlation plot, performs the fitting and scoring process, and performs goodness of fit tests on the top scoring distribution and displays all the results by opening a browser window. The generatedhtmlfile is stored in theKSL.plotDirdirectory using the supplied name as the pre-fix for a temporary file. This one function performs all the necessary fitting steps and returns the results, including plots, within anhtmlpage.
The PDFModeling class encapsulates the estimation and scoring process. The purpose of this class is to serve as the general location for implementing the estimation of distribution parameters across many distributions. The general use involves the following:
val d = PDFModeler(data)
val estimationResults: List<EstimationResult> = d.estimateParameters(d.allEstimators)
val scoringResults = d.scoringResults(estimationResults)
val model = d.evaluateScoringResults(scoringResults)
scoringResults.forEach( ::println)The scoring results will be updated with the evaluation information and will contain the evaluation scores. The scoring results can be sorted to find the recommended distribution based on the evaluation score. Alternatively, the single function can be used:
This function returns an instance of PDFModelingResults, which will have the results of the entire fitting process. The advantage of using the individual functions may permit some further customization of the estimation process. The PDFModelingResults class in Figure 2.9 is a data class that holds all of the results from the fitting and scoring process. In addition, the class holds an instance of the scoring model (AdditiveMODAModel), which can be used to perform additional analysis of the scores. The property sortedScoringResults provides the list of results sorted such that the top performer is the first element of the list.
To summarize, the KSL continuous distribution modeling framework allows the modeler to:
- Define and select from a set of distributions to evaluate
- Define and select from a set of parameter estimation methods
- Compute bootstrap estimates of the confidence intervals for the estimated parameters
- Define and select from a set of distribution fit quality metrics (scoring models)
- Combine scoring models into an overall measure
- Recommend the best distribution based on weighted preference among evaluation metrics
- Make observations plots, histograms, autocorrelation plots, P-P plots, Q-Q plots, and empirical distribution plots.
All of this functionality is encapsulated in the PDFModeler class. This functionality will be illustrated in Section 2.4.4.
After performing the estimation and scoring process, the modeler may want to perform statistical tests for the top performing distribution (or others). The ContinuousCDFGoodnessOfFit class facilitates the performing of the following goodness of fit tests:
- Chi-Squared
- Kolmogorov-Smirnov
- Anderson-Darling
- Cramer-Von Mises
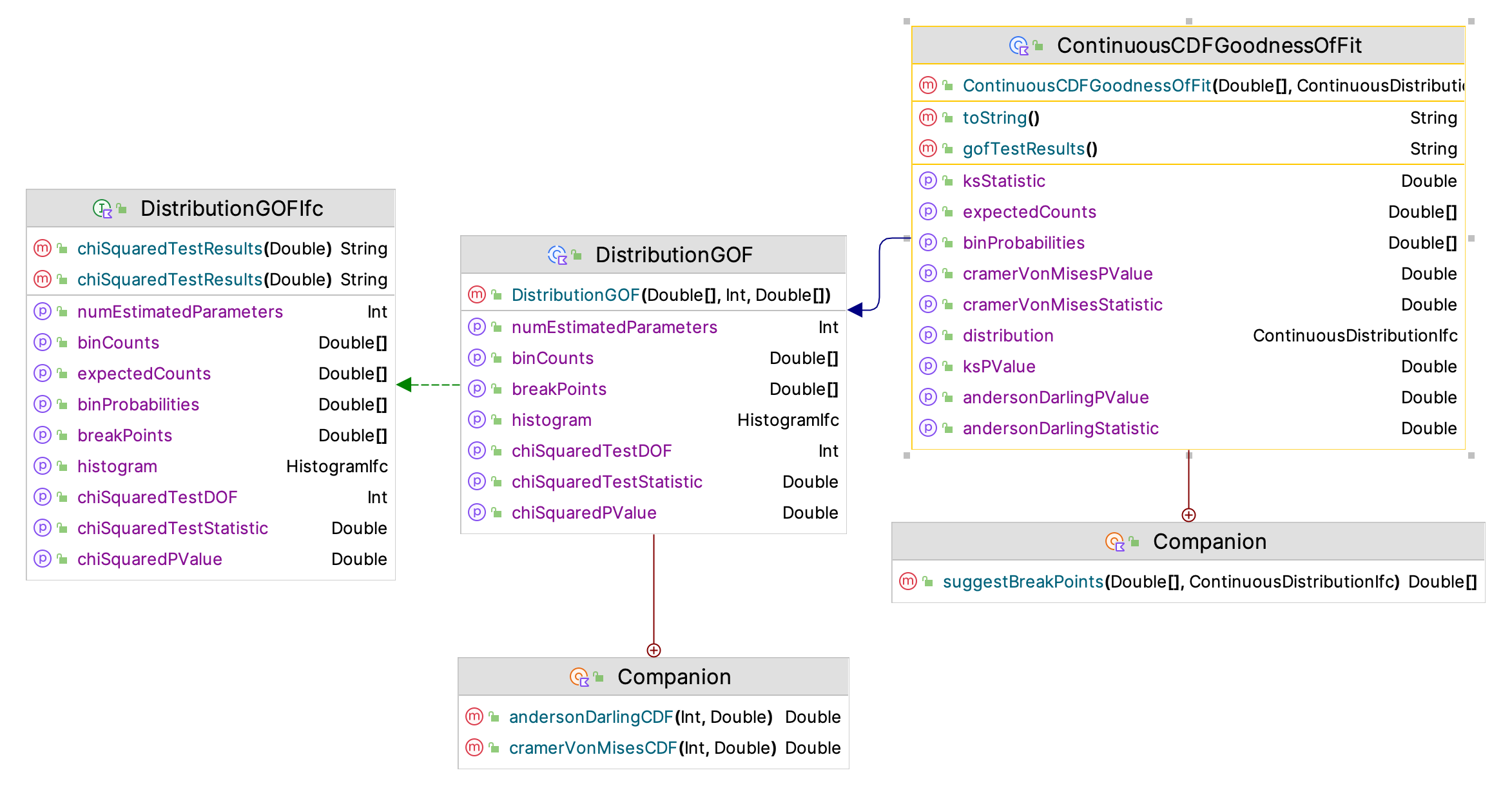
Figure 2.10: Continuous Distribution Goodness of Fit Framework
Figure 2.10 shows the framework of classes and interfaces for performing goodness of fit tests within the KSL. The main class is the ContinuousCDFGoodnessOfFit class. This class will compute the test statistics and their P-values.
The chi-squared test is the most challenging test to execute in an automated fashion. The KSL follows the recommendation found in Chapter 6 of (Law 2007) for setting up the chi-squared test. The KSL does not use arbitrary break points from a histogram generation process. Instead the KSL attempts to define the break points for the chi-squared intervals such that each interval has the same probability of occurrence. This also ensures that the expected number of observations within each interval is approximately the same. The theoretical basis for this approach can be found in (Williams 1950). (Williams 1950) considered the testing of \(U(0,1)\) random variates. In the case of the \(U(0,1)\) distribution, the choice of the number of intervals determines the break points because each interval is equally likely. (Williams 1950) recommended choosing the class limits such that the expected number in the interval was \(n/k\), where \(n\) is the number of observations and \(k\) is the number of class intervals. Based on the ability to ensure that the resulting chi-squared test statistic actually has a chi-squared distribution, (Williams 1950) recommended that the number of class intervals be:
\[\begin{equation} k = \Bigg\lceil 4 \, \sqrt[5]{\frac{2(n-1)^2}{z_{1-\alpha}}} \, \Bigg\rceil \end{equation}\]
This approach produces equally distant break points between \((0,1)\). Let’s call those break points \(u_i\) for \(i=1,\cdots,k\). We then define the break points for the chi-squared test for the distribution, \(F(x)\), as \(b_i = F^{-1}(u_i)\), which will result in non-equally spaced break points for \(F(x)\), but the probability \(p_i\) associated with the intervals will all be the same. For the resulting recommended break points, the procedure attempts to ensure that the number of intervals is at least 3 and that the expected number within the intervals is at least 5. If the number of observations of the sample, \(n\), is less than or equal to 15, this may not be possible. The procedure ensures that there are at least 3 intervals and if the expected count is less than 5 for any interval the user is warned. This same procedure is used in determining the break points for the squared error criteria. This approach reduces the sensitivity of the chi-squared fitting process and the squared error criteria to the choice of the intervals. This functionality is found in the suggestBreakPoints() function of the companion object of the ContinuousCDFGoodnessOfFit class.
As an example, the following code generates an exponentially distributed sample and applies the goodness of fit tests to the data.
Example 2.24 (Goodness of Fit Testing)
The results, as expected, indicate that the data is exponentially distributed. Notice how the binning process for the data results in the bin probabilities and expected number per bin being all equal. The observed counts look pretty consistent for the intervals. Thus, the chi-squared test does not reject the hypothesis that the data is exponential with a mean of 10. In addition, the Anderson-Darling, K-S test, and Cramer Von Mises P-values indicate that we should not reject the hypothesis that the data is exponentially distributed. The showAllResultsInBrowser() function of the PDFModeler class automatically performs these goodness of fit tests for the recommended distribution from the PDF modeling process.
GOF Results for Distribution: Exponential(mean=10.0)
---------------------------------------------------------
Chi-Squared Test Results:
Bin Label P(Bin) Observed Expected
1 [ 0.00, 0.17) 0.016949 20 16.9492
2 [ 0.17, 0.34) 0.016949 14 16.9492
3 [ 0.34, 0.52) 0.016949 23 16.9492
4 [ 0.52, 0.70) 0.016949 14 16.9492
5 [ 0.70, 0.89) 0.016949 21 16.9492
6 [ 0.89, 1.07) 0.016949 21 16.9492
7 [ 1.07, 1.26) 0.016949 22 16.9492
8 [ 1.26, 1.46) 0.016949 10 16.9492
9 [ 1.46, 1.66) 0.016949 18 16.9492
10 [ 1.66, 1.86) 0.016949 12 16.9492
11 [ 1.86, 2.06) 0.016949 16 16.9492
12 [ 2.06, 2.27) 0.016949 12 16.9492
13 [ 2.27, 2.49) 0.016949 23 16.9492
14 [ 2.49, 2.71) 0.016949 15 16.9492
15 [ 2.71, 2.93) 0.016949 17 16.9492
16 [ 2.93, 3.16) 0.016949 14 16.9492
17 [ 3.16, 3.40) 0.016949 21 16.9492
18 [ 3.40, 3.64) 0.016949 13 16.9492
19 [ 3.64, 3.89) 0.016949 11 16.9492
20 [ 3.89, 4.14) 0.016949 20 16.9492
21 [ 4.14, 4.40) 0.016949 18 16.9492
22 [ 4.40, 4.67) 0.016949 19 16.9492
23 [ 4.67, 4.94) 0.016949 23 16.9492
24 [ 4.94, 5.22) 0.016949 19 16.9492
25 [ 5.22, 5.51) 0.016949 17 16.9492
26 [ 5.51, 5.81) 0.016949 18 16.9492
27 [ 5.81, 6.12) 0.016949 12 16.9492
28 [ 6.12, 6.44) 0.016949 17 16.9492
29 [ 6.44, 6.76) 0.016949 16 16.9492
30 [ 6.76, 7.10) 0.016949 13 16.9492
31 [ 7.10, 7.45) 0.016949 18 16.9492
32 [ 7.45, 7.82) 0.016949 17 16.9492
33 [ 7.82, 8.19) 0.016949 21 16.9492
34 [ 8.19, 8.59) 0.016949 17 16.9492
35 [ 8.59, 8.99) 0.016949 25 16.9492
36 [ 8.99, 9.42) 0.016949 9 16.9492
37 [ 9.42, 9.86) 0.016949 14 16.9492
38 [ 9.86,10.33) 0.016949 15 16.9492
39 [10.33,10.82) 0.016949 13 16.9492
40 [10.82,11.33) 0.016949 12 16.9492
41 [11.33,11.87) 0.016949 18 16.9492
42 [11.87,12.44) 0.016949 23 16.9492
43 [12.44,13.05) 0.016949 20 16.9492
44 [13.05,13.69) 0.016949 9 16.9492
45 [13.69,14.38) 0.016949 14 16.9492
46 [14.38,15.13) 0.016949 16 16.9492
47 [15.13,15.93) 0.016949 13 16.9492
48 [15.93,16.80) 0.016949 22 16.9492
49 [16.80,17.75) 0.016949 15 16.9492
50 [17.75,18.80) 0.016949 18 16.9492
51 [18.80,19.98) 0.016949 23 16.9492
52 [19.98,21.32) 0.016949 23 16.9492
53 [21.32,22.86) 0.016949 25 16.9492
54 [22.86,24.68) 0.016949 9 16.9492
55 [24.68,26.91) 0.016949 14 16.9492
56 [26.91,29.79) 0.016949 16 16.9492
57 [29.79,33.84) 0.016949 15 16.9492
58 [33.84,40.78) 0.016949 15 16.9492
59 [40.78,155.00) 0.016949 22 16.9490
Number of estimated parameters = 1
Number of intervals = 59
Degrees of Freedom = 57
Chi-Squared Test Statistic = 61.52812706136465
P-value = 0.31723313805973075
Hypothesis test at 0.05 level:
The p-value = 0.31723313805973075 is >= 0.05 : Do not reject hypothesis.
Goodness of Fit Test Results:
K-S test statistic = 0.017687069238841113
K-S test p-value = 0.9075526348536717
Anderson-Darling test statistic = 0.3610051171259556
Anderson-Darling test p-value = 0.8863125779601514
Cramer-Von-Mises test statistic = 0.043345445388941854
Cramer-Von-Mises test p-value = 0.91528156463299592.4.3 Discrete Distribution Framework
For discrete distributions, the KSL provides the PMFModeler class. Since there are less discrete distributions within the KSL than continuous distributions, the PMFModeler class does not provide the full range of functionality provided by the PDFModeler class. Instead the PMFModeler class focuses on estimating the parameters of discrete distributions. Similar to how the PDFModeler class functions, the PMFModeler has an estimateParameters() function that uses a set of objects that implement the ParameterEstimatorIfc interface. The default set of discrete distributions includes the Poisson, negative binomial, and the binomial distributions. Of course users can define additional discrete distributions and implement parameter estimators for those distributions.
Figure 2.11 presents the PMF estimation framework. As indicated the key function is the estimateParameters() function. Note also that the companion object for the PMFModeler class has the function equalizedPMFBreakPoints(), which can be useful during the goodness of fit testing of the distribution. The purpose of the function is to attempt to form intervals that have similar probabilities.
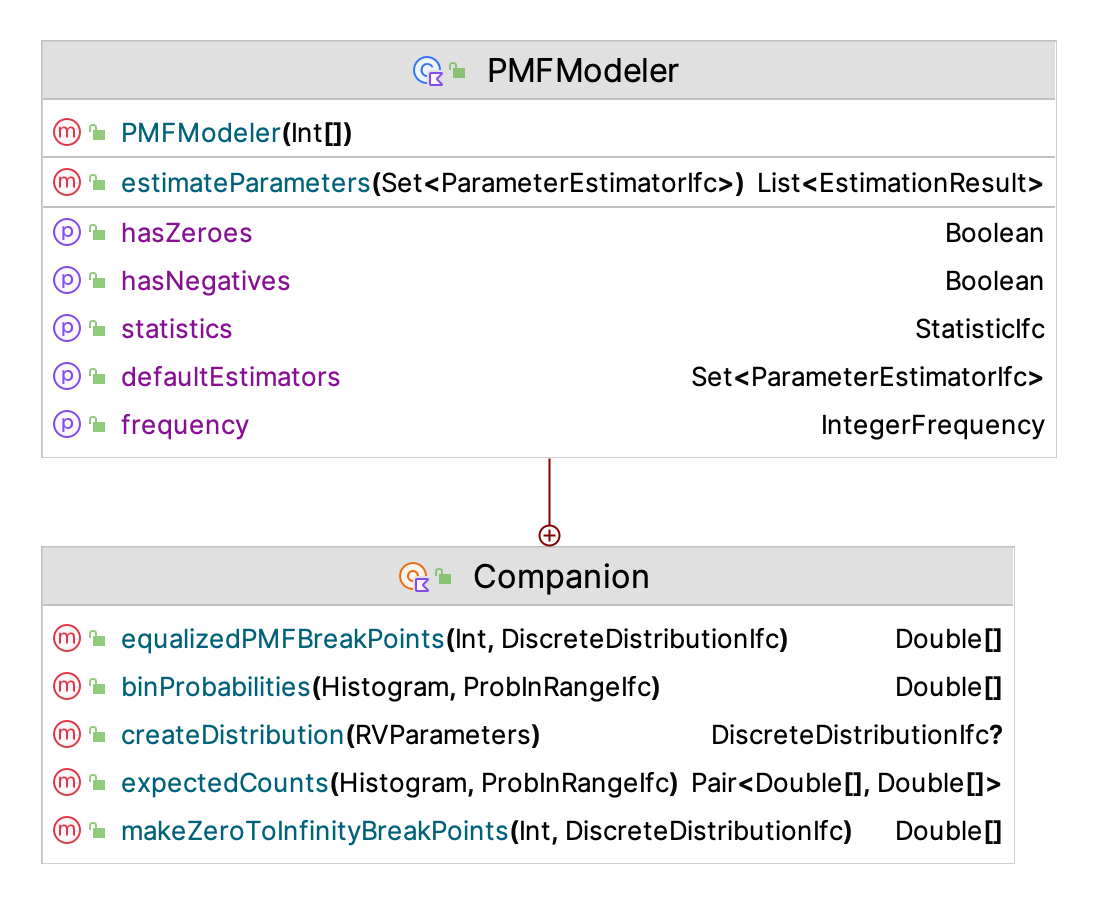
Figure 2.11: PMF Estimation Framework
The application of the estimateParameters() function results in the creation of a list that contains instances of EstimationResult, one for each of the estimation methods.
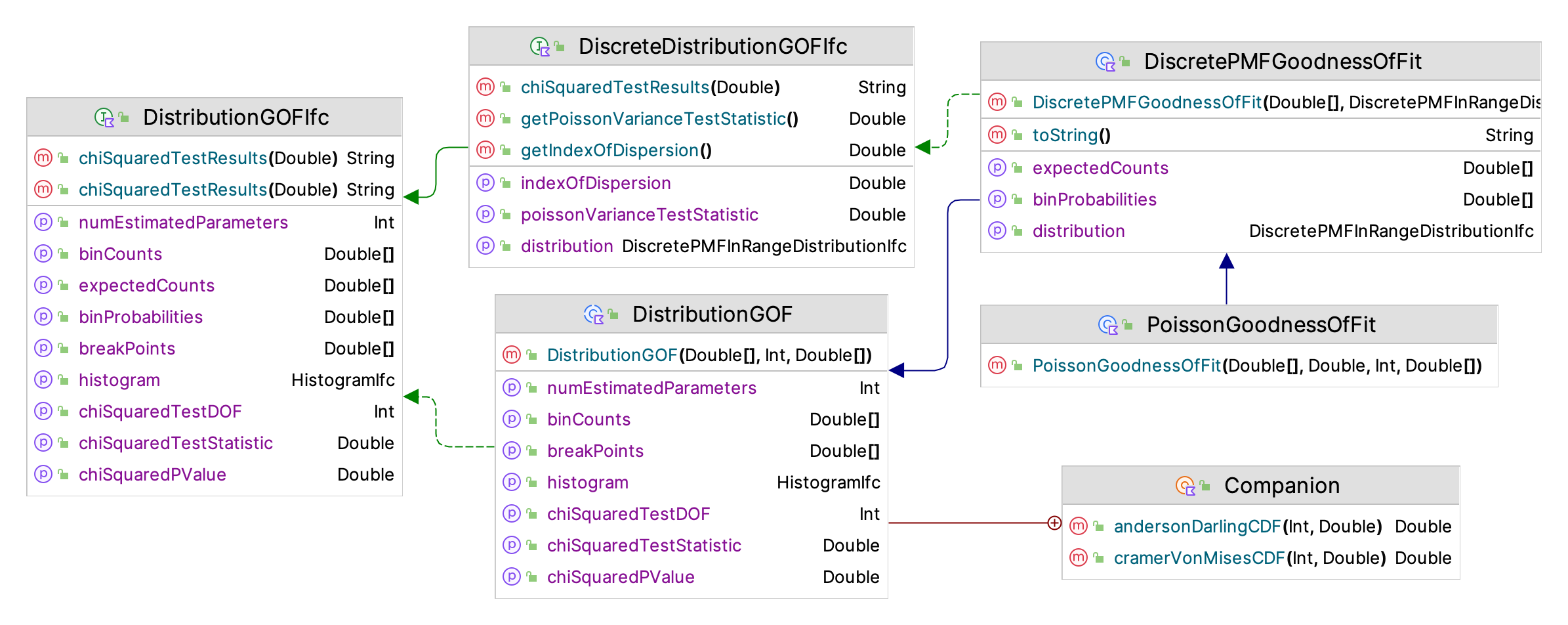
Figure 2.12: Discrete Distribution Goodness of Fit Framework
Given the limited number of discrete distributions, the KSL does not provide a scoring model approach for selecting the best distribution. Instead, the DiscretePMFGoodnessOfFit class, illustrated in Figure 2.12 can be used to check the goodness of fit for the discrete distribution. The primary method for testing the goodness of it is the chi-squared goodness of fit test. Similar to how the continuous distribution defines break points that result in approximately equal probabilities for the bins and expected counts, the KSL attempts to form intervals for the chi-squared test that have approximately equal probabilities. The following code illustrates how to fit a negative binomial distribution to some randomly generated data.
Example 2.25 (Discrete Goodness of Fit Testing)
val dist = NegativeBinomial(0.2, theNumSuccesses = 4.0)
val rv = dist.randomVariable
rv.advanceToNextSubStream()
val data = rv.sample(200)
val breakPoints = PMFModeler.makeZeroToInfinityBreakPoints(data.size, dist)
val pf = DiscretePMFGoodnessOfFit(data, dist, breakPoints = breakPoints)
println(pf.chiSquaredTestResults())The results indicate the challenge of trying to make bins with equal probability for discrete distributions. In general, it may not be possible to do so. Thus, the modeler is encouraged to update the break points as needed during the distribution assessment process. As expected the results indicate that we should not reject the hypothesis of a negative binomial distribution for this situation.
Chi-Squared Test Results:
Bin Label P(Bin) Observed Expected
1 [ 0.00, 3.00) 0.016960 4 3.39200 *** Warning: expected < 5 ***
2 [ 3.00, 5.00) 0.039322 7 7.86432
3 [ 5.00, 6.00) 0.029360 10 5.87203
4 [ 6.00, 7.00) 0.035232 7 7.04643
5 [ 7.00, 8.00) 0.040265 7 8.05306
6 [ 8.00, 9.00) 0.044292 5 8.85837
7 [ 9.00,10.00) 0.047245 10 9.44893
8 [10.00,11.00) 0.049134 9 9.82689
9 [11.00,12.00) 0.050028 6 10.0056
10 [12.00,13.00) 0.050028 11 10.0056
11 [13.00,14.00) 0.049258 6 9.85162
12 [14.00,15.00) 0.047851 12 9.57015
13 [15.00,16.00) 0.045937 7 9.18734
14 [16.00,17.00) 0.043640 17 8.72798
15 [17.00,18.00) 0.041073 4 8.21457
16 [18.00,19.00) 0.038335 7 7.66693
17 [19.00,20.00) 0.035510 7 7.10200
18 [20.00,21.00) 0.032669 9 6.53384
19 [21.00,22.00) 0.029869 5 5.97379
20 [22.00,23.00) 0.027154 3 5.43072
21 [23.00,24.00) 0.024556 4 4.91126 *** Warning: expected < 5 ***
22 [24.00,26.00) 0.041903 13 8.38058
23 [26.00,28.00) 0.033376 9 6.67520
24 [28.00,31.00) 0.036998 6 7.39969
25 [31.00,36.00) 0.036799 7 7.35973
26 [36.00,Infinity) 0.033207 8 6.64147
Number of estimated parameters = 2
Number of intervals = 26
Degrees of Freedom = 23
Chi-Squared Test Statistic = 25.69659399548871
P-value = 0.31539706650371313
Hypothesis test at 0.05 level:
The p-value = 0.31539706650371313 is >= 0.05 : Do not reject hypothesis.2.4.4 Illustrative Examples from Appendix B
This section illustrates how to use the KSL probability distribution modeling frameworks by applying the previously discussed constructs to two examples from Appendix B. We will start with the fitting of Poisson distribution to the data from Example B.1, which is repeated here for convenience. The data associated with the examples of this section can be found in the chapter files with in the KSLExamples project associated with the KSL source code repository.
NOTE! Distribution fitting often requires visualizing the data. The KSL provides support for making plots via the lets-plot library. Section D.8 of Appendix D illustrates the basics of KSL plotting functionality. This section illustrates some plots that are important for distribution modeling.
Example 2.26 (Fitting a Poisson Distribution) Suppose that we are interested in modeling the demand for a computer laboratory during the morning hours between 9 am to 11 am on normal weekdays. During this time a team of undergraduate students has collected the number of students arriving to the computer lab during 15 minute intervals over a period of 4 weeks.
Since there are four 15 minute intervals in each hour for each two hour time period, there are 8 observations per day. Since there are 5 days per week, we have 40 observations per week for a total of \(40\times 4= 160\) observations. A sample of observations per 15 minute interval are presented in Table 2.1. The full data set is available with the chapter files. Check whether a Poisson distribution is an appropriate model for this data.
| Week | Period | M | T | W | TH | F |
|---|---|---|---|---|---|---|
| 1 | 9:00-9:15 am | 8 | 5 | 16 | 7 | 7 |
| 1 | 9:15-9:30 am | 8 | 4 | 9 | 8 | 6 |
| 1 | 9:30-9:45 am | 9 | 5 | 6 | 6 | 5 |
| 1 | 9:45-10:00 am | 10 | 11 | 12 | 10 | 12 |
| 1 | 10:00-10:15 am | 6 | 7 | 14 | 9 | 3 |
| 1 | 10:15-10:30 am | 11 | 8 | 7 | 7 | 11 |
| 1 | 10:30-10:45 am | 12 | 7 | 8 | 3 | 6 |
| 1 | 10:45-11:00 am | 8 | 9 | 9 | 8 | 6 |
| 2 | 9:00-9:15 am | 10 | 13 | 7 | 7 | 7 |
| 3 | 9:00-9:15 am | 5 | 7 | 14 | 8 | 8 |
| 4 | 9:00-9:15 am | 7 | 11 | 8 | 5 | 4 |
| 4 | 10:45-11:00 am | 8 | 9 | 7 | 9 | 6 |
Since the testing of dependence on the day of the week or the period of observation was already performed in Appendix B, we focus on the distribution fitting process in this demonstration of the KSL constructs. Here, we need to fit a Poisson distribution to the data. The first step is reading the data from the CSV file. This can be readily accomplished by using the CSV file reading capabilities of Kotlin’s DataFrame library. The following code uses the KSL’s KSLFileUtil object to open a file choosing dialog for the user to select the file, which then has its contents read in using the CSV file processing function for the DataFrame object. This data is converted into an integer array and returned. A discussion of CSV file processing and data frames can be found in Sections D.4 and D.5 of Appendix D.
fun readCountData(): IntArray {
// choose file: KSL/KSLExamples/chapterFiles/Appendix-Distribution Fitting/PoissonCountData.csv
val file = KSLFileUtil.chooseFile()
if (file != null) {
val df = DataFrame.readCSV(
file,
colTypes = mapOf(
"week" to ColType.Int,
"period" to ColType.Int,
"day" to ColType.String,
"count" to ColType.Int
)
)
val count by column<Int>()
val countData: DataColumn<Int> = df[count]
return countData.toIntArray()
}
return IntArray(0)
}Once the data is an array, the KSL’s discrete distribution framework can be easily applied. In the following code, the data is used to visualize the count data in the form of an integer frequency plot, which we can use like a histogram to view the distribution of the data and see if it has a shape that would support the hypothesis of a Poisson distribution.
val data = readCountData()
val f = IntegerFrequency(data)
val fp = f.frequencyPlot()
fp.showInBrowser()
fp.saveToFile("Lab_Count_Freq_Plot")Figure 2.13 clearly indicates that the Poisson distribution is a candidate model.
Figure 2.13: Integer Frequency Plot of Lab Count Data
The following code will create a time series observation plot of the data and an auto correlation plot of the data. The use of both of these plots for analysis of data is discussed in Appendix B. This code will also save the plots to files and display the plots within a browser window.
val op = ObservationsPlot(data)
op.saveToFile("Lab_Count_Obs_Plot")
op.showInBrowser()
val acf = ACFPlot(data.toDoubles())
acf.saveToFile("Lab_Count_ACF_Plot")
acf.showInBrowser()
println(f)Just as in Appendix B, the time series plot does not indicate a trend or pattern with respect to time as shown in Figure 2.14.
Figure 2.14: Time Series Plot of Lab Count Data
Again, the ACF plot, see Figure 2.15, does not indicate that the data has any significant concerns with respect to autocorrelation.
Figure 2.15: Autocorrelation Plot of Lab Count Data
Because the plots indicate that the data is likely to be independent and identically distributed, it appears that it should be safe to proceed with the distribution modeling task. The following code will estimate the parameters, perform a goodness of fit test, and display a plot that compares the theoretical PMF to the empirical PMF.
val pmfModeler = PMFModeler(data)
val results = pmfModeler.estimateParameters(setOf(PoissonMLEParameterEstimator))
val e = results.first()
println(e)
val mean = e.parameters!!.doubleParameter("mean")
val pf = PoissonGoodnessOfFit(data.toDoubles(), mean = mean)
println(pf)
val plot = PMFComparisonPlot(data, pf.distribution)
plot.saveToFile("Lab_Count_PMF_Plot")
plot.showInBrowser()The code first creates an instance of the PMFModeler class to perform the estimation. In this situation, only the estimator for the Poisson distribution is specified as input to the estimateParameters() function. The estimated mean of the distribution is extracted from the estimated parameters and used for the PoissonGoodnessOfFit class. The PoissonGoodnessOfFit class is a straight-forward sub-class of DiscretePMFGoodnessOfFit class. The results of the fit are printed and then the PMF comparison plot is created.
Shift estimation results:
null
Estimated parameters:
RV Type = Poisson
Double Parameters {mean=8.275000000000002}
Integer Parameters {}
Double Array Parameters {}
Chi-Squared Test Results:
Bin Label P(Bin) Observed Expected
1 [ 0.00, 4.00) 0.035151 6 5.62421
2 [ 4.00, 5.00) 0.049782 7 7.96515
3 [ 5.00, 6.00) 0.082390 13 13.1823
4 [ 6.00, 7.00) 0.113629 16 18.1806
5 [ 7.00, 8.00) 0.134326 21 21.4921
6 [ 8.00, 9.00) 0.138943 25 22.2309
7 [ 9.00,10.00) 0.127750 20 20.4401
8 [10.00,11.00) 0.105713 21 16.9141
9 [11.00,12.00) 0.079525 11 12.7241
10 [12.00,13.00) 0.054839 7 8.77429
11 [13.00,14.00) 0.034907 5 5.58518
12 [14.00,Infinity) 0.043044 8 6.88700
Number of estimated parameters = 1
Number of intervals = 12
Degrees of Freedom = 10
Chi-Squared Test Statistic = 2.5923612067415056
P-value = 0.9894603477732713
Hypothesis test at 0.05 level:
The p-value = 0.9894603477732713 is >= 0.05 : Do not reject hypothesis.
Figure 2.16: PMF Comparison Plot of Lab Count Data
The results of the goodness of fit test and the PMF comparison plot, Figure 2.16, clearly indicate that the Poisson distribution should not be rejected as a model for this data.
The follow example repeats the analysis of Section B.5.6 on the pharmacy service time data using KSL constructs.
Example 2.27 (Analyzing the Pharmacy Data using the KSL) One hundred observations of the service time were collected using a portable digital assistant and are shown in Table 2.2 where the first observation is in row 1 column 1, the second observation is in row 2 column 1, the \(21^{st}\) observation is in row 1 column 2, and so forth.
| 61 | 278.73 | 194.68 | 55.33 | 398.39 |
| 59.09 | 70.55 | 151.65 | 58.45 | 86.88 |
| 374.89 | 782.22 | 185.45 | 640.59 | 137.64 |
| 195.45 | 46.23 | 120.42 | 409.49 | 171.39 |
| 185.76 | 126.49 | 367.76 | 87.19 | 135.6 |
| 268.61 | 110.05 | 146.81 | 59 | 291.63 |
| 257.5 | 294.19 | 73.79 | 71.64 | 187.02 |
| 475.51 | 433.89 | 440.7 | 121.69 | 174.11 |
| 77.3 | 211.38 | 330.09 | 96.96 | 911.19 |
| 88.71 | 266.5 | 97.99 | 301.43 | 201.53 |
| 108.17 | 71.77 | 53.46 | 68.98 | 149.96 |
| 94.68 | 65.52 | 279.9 | 276.55 | 163.27 |
| 244.09 | 71.61 | 122.81 | 497.87 | 677.92 |
| 230.68 | 155.5 | 42.93 | 232.75 | 255.64 |
| 371.02 | 83.51 | 515.66 | 52.2 | 396.21 |
| 160.39 | 148.43 | 56.11 | 144.24 | 181.76 |
| 104.98 | 46.23 | 74.79 | 86.43 | 554.05 |
| 102.98 | 77.65 | 188.15 | 106.6 | 123.22 |
| 140.19 | 104.15 | 278.06 | 183.82 | 89.12 |
| 193.65 | 351.78 | 95.53 | 219.18 | 546.57 |
Recall the basic process described in Appendix B. We will plot the data using a histogram, make a time series observation plot, and make an ACF plot. The following code performs those tasks. The plots can be shown in a browser window or saved to files.
val data = KSLFileUtil.scanToArray(myFile.toPath())
val d = PDFModeler(data)
println(d.histogram)
println()
val hPlot = d.histogram.histogramPlot()
hPlot.showInBrowser()
val op = ObservationsPlot(data)
op.showInBrowser()
val acf = ACFPlot(data)
acf.showInBrowser()This results in the following histogram summary, which clearly indicates that the data is shifted from zero to about 36.
-------------------------------------
Number of bins = 6
First bin starts at = 36.0
Last bin ends at = 786.0
Under flow count = 0.0
Over flow count = 0.0
Total bin count = 100.0
Total count = 100.0
-------------------------------------
Bin Range Count CumTot Frac CumFrac
1 [36.00,161.00) = 60 60.0 0.600000 0.600000
2 [161.00,286.00) = 22 82.0 0.220000 0.820000
3 [286.00,411.00) = 10 92.0 0.100000 0.920000
4 [411.00,536.00) = 6 98.0 0.060000 0.980000
5 [536.00,661.00) = 1 99.0 0.010000 0.990000
6 [661.00,786.00) = 1 100.0 0.010000 1.000000
-------------------------------------Figure 2.17 clearly shows an exponential shape for the distribution.
Figure 2.17: Histogram of the Pharmacy Data
Similar to the analysis in Appendix B, the time series plot, Figure 2.18, and the ACF plot, Figure 2.19 do not indicate any issues with non-stationary behavior or with dependence within the observations.
Figure 2.18: Time Series Observation Plot for Pharmacy Data
Figure 2.19: ACF Plot for Pharmacy Data
Given this analysis, we can proceed with modeling the distribution and checking for the goodness of fit. The following KSL code will estimate the parameters of the default distributions within the KSL and recommend a candidate distribution. Notice that the shift parameter will be automatically estimated for this situation.
val results = d.estimateAndEvaluateScores()
println("PDF Estimation Results for each Distribution:")
println("------------------------------------------------------")
results.sortedScoringResults.forEach(::println)
val topResult = results.sortedScoringResults.first()
val scores = results.evaluationModel.alternativeScoresAsDataFrame("Distributions")
println(scores)
println()
val values = results.evaluationModel.alternativeValuesAsDataFrame("Distributions")
println(values)
println()
val distPlot = topResult.distributionFitPlot()
distPlot.showInBrowser("Recommended Distribution ${topResult.name}")
println()
println("** Recommended Distribution** ${topResult.name}")
println()The following table displays the distribution fitting scores for the Bayesian Information Criterion (BIC), Anderson-Darling (AD), Cramer Von Mises (CVM), and Q-Q plot correlation criteria.
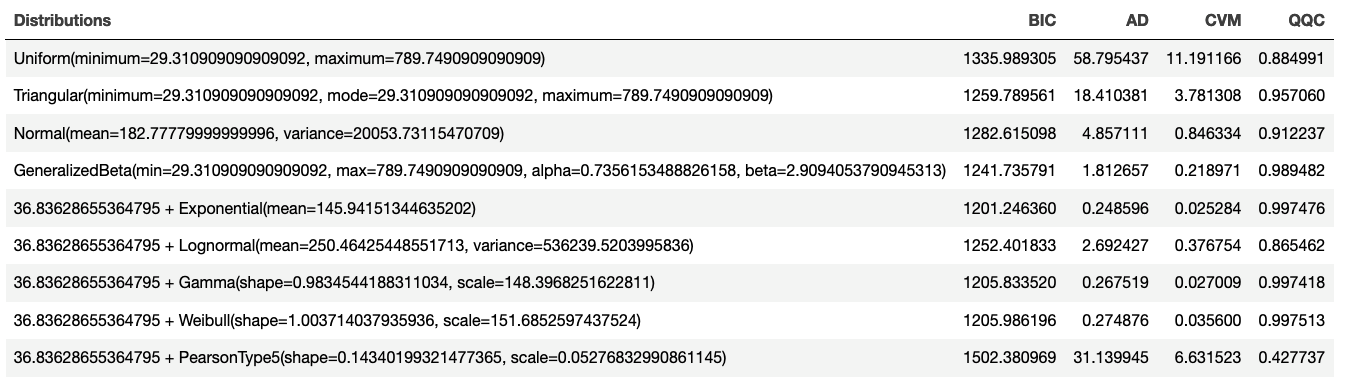
Figure 2.20: Scoring Model Results
By applying the value scoring model and sorting, we can see in Figure 2.21 that the top performing distribution is the exponential distribution with an overall value of 0.9484545. Thus, the recommended distribution is: 36.83628655364795 + Exponential(mean=145.94151344635202). Notice that the shift parameter was automatically estimated for this situation.
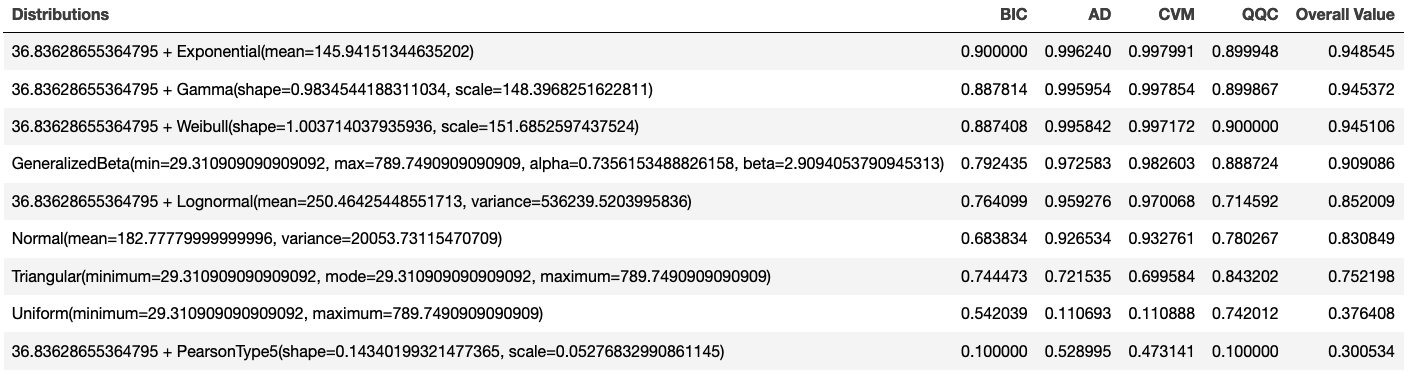
Figure 2.21: Overall Scoring Results
The KSL distribution recommendation framework also evaluates each distribution based on the rank obtained by each metric. The distribution that had the most first place ranks can be considered the top performing distribution. As shown in Figure 2.22, we again see that the exponential distribution is the top distribution based on rankings.
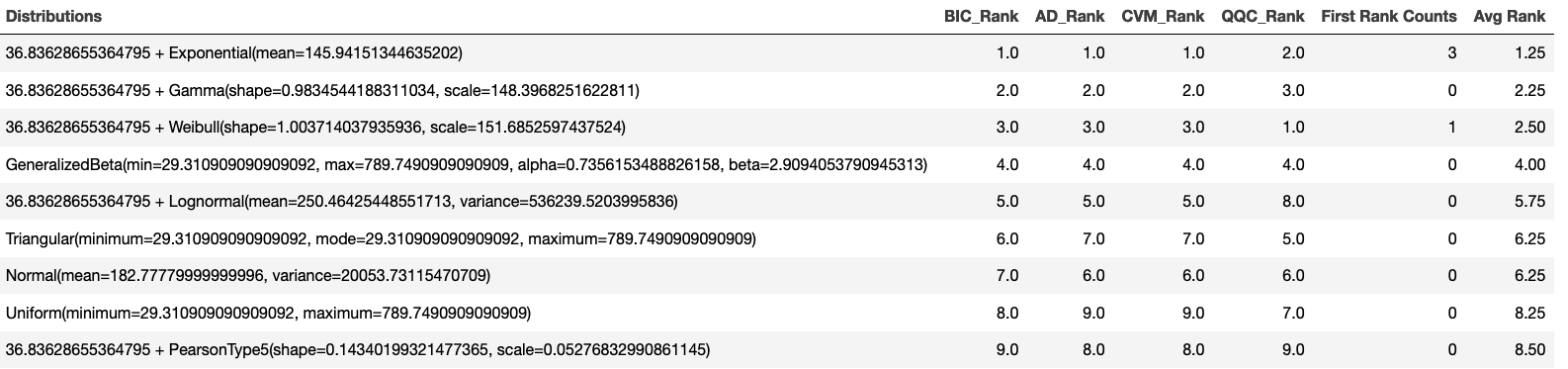
Figure 2.22: Overall Ranking Results
If you are unsure of the recommended distribution or you want to better understand the sensitivity of the recommendation, the PDFModeler companion object provides support for bootstrapping the distribution family recommendation. Assuming that the observations are in an array called data, the following code will repeatedly sample from the data using a bootstrapping approach to tabulate the frequency that each possible distribution is recommended by the framework.
Running the bootstrapping family frequency tabulation process on the pharamacy model data yields the following results.
Distribution Ranked First cum_count proportion cumProportion
0 Triangular 1.0 1.0 0.0025 0.002500
1 GeneralizedBeta 2.0 3.0 0.0050 0.007500
2 Exponential 321.0 324.0 0.8025 0.810000
3 Gamma 76.0 400.0 0.1900 1.000000Clearly, the exponential distribution is the most likely distribution to be recommended using the average scoring criterion. This process can be used before going through the PDF modeling process to suggest distributions to consider, or, as done here, it can be performed after the distribution recommendation process to provide some confidence in the recommended distribution.
After we are comfortable with the recommended distribution, we can use the following code to perform a goodness of fit analysis.
val gof = ContinuousCDFGoodnessOfFit(topResult.estimationResult.testData,
topResult.distribution,
numEstimatedParameters = topResult.numberOfParameters
)
println(gof)The results of the goodness of fit analysis clearly indicate that we should not reject the exponential distribution. Notice that the results are for the shifted distribution.
GOF Results for Distribution: Exponential(mean=145.94151344635202)
---------------------------------------------------------
Chi-Squared Test Results:
Bin Label P(Bin) Observed Expected
1 [ 0.00, 7.49) 0.050000 3 5.00000
2 [ 7.49,15.38) 0.050000 4 5.00000
3 [15.38,23.72) 0.050000 8 5.00000
4 [23.72,32.57) 0.050000 3 5.00000
5 [32.57,41.98) 0.050000 8 5.00000
6 [41.98,52.05) 0.050000 4 5.00000
7 [52.05,62.87) 0.050000 5 5.00000
8 [62.87,74.55) 0.050000 8 5.00000
9 [74.55,87.25) 0.050000 4 5.00000
10 [87.25,101.16) 0.050000 2 5.00000
11 [101.16,116.54) 0.050000 9 5.00000
12 [116.54,133.72) 0.050000 3 5.00000
13 [133.72,153.21) 0.050000 4 5.00000
14 [153.21,175.71) 0.050000 6 5.00000
15 [175.71,202.32) 0.050000 3 5.00000
16 [202.32,234.88) 0.050000 4 5.00000
17 [234.88,276.87) 0.050000 7 5.00000
18 [276.87,336.04) 0.050000 4 5.00000
19 [336.04,437.20) 0.050000 5 5.00000
20 [437.20,1596.00) 0.049982 6 4.99822 *** Warning: expected < 5 ***
Number of estimated parameters = 1
Number of intervals = 20
Degrees of Freedom = 18
Chi-Squared Test Statistic = 16.000784446070348
P-value = 0.5924925929222188
Hypothesis test at 0.05 level:
The p-value = 0.5924925929222188 is >= 0.05 : Do not reject hypothesis.
Goodness of Fit Test Results:
K-S test statistic = 0.0399213095618332
K-S test p-value = 0.9954253138552503
Anderson-Darling test statistic = 0.24859556182926212
Anderson-Darling test p-value = 0.9710833730000956
Cramer-Von-Mises test statistic = 0.025283543923658194
Cramer-Von-Mises test p-value = 0.9893094979248238Finally, we can review the distribution plot, Figure 2.23, and see that according the the P-P plot, Q-Q plot, histogram overlay, and empirical cumulative distribution overlay plot that the exponential distribution is an excellent probability model for this data.
Figure 2.23: Distribution Plot for Pharmacy Data
As a final note for this example, all of the previously illustrated analysis can be performed with a few lines of code:
val data = KSLFileUtil.scanToArray(myFile.toPath())
val d = PDFModeler(data)
d.showAllResultsInBrowser()The functionally for distribution modeling within the KSL is on par with what you can find within commercial software.