8.3 Generating Multi-Variate and Correlated Random Variates

The purpose of this section is to present the KSL constructs that facilitate the sampling from multi-variate distributions. In order to do this, we will discuss some of the common methods for generating correlated random variables. We will focus on those techniques that have implementations within the KSL. The presentation will be focused on the practical application of the methods rather than the theory. Because it will be instructive, we will start with generating from bi-variate distributions, specifically the bi-variate normal distribution.

8.3.1 Generating from a Bivariate Normal Distribution

A bivariate normal distribution is specified by the expected values, variances, and correlation between the random variables. For an excellent refresher on the mathematical basis for bivariate normal random variables, we refer the reader to (Pishro-Nik 2014) and specifically Section 5.3.2.

We specify a bivariate normal random variables as \((X_1, X_2) \sim BVN(\mu_1, \sigma^2_1,\mu_2, \sigma^2_2,\rho)\). The key result necessary for generating BVN random variables is the following procedure:

  1. Let \(Z_1\) and \(Z_2\) be independent \(N(0,1)\) random variables.
  2. Define \(X_1 = \sigma_1 Z_1 + \mu_1\) and \(X_2 = \sigma_2(\rho Z_1 + \sqrt{(1-\rho^2)} Z_2) + \mu_2\), where \(-1<\rho<1\).
  3. Then, \((X_1, X_2) \sim BVN(\mu_1, \sigma^2_1,\mu_12, \sigma^2_2,\rho)\)

An outline for the proof of this result can be found in (Pishro-Nik 2014), Section 5.3.2. Thus, if we can generate independent standard normal random variables, we can generate bivariate normal random variables via simple algebra. As can be seen in the following code, the KSL BivariateNormalRV class uses this procedure to generate an array that contains the bivariate normal sample.

class BivariateNormalRV(
    val mean1: Double = 0.0,
    val v1: Double = 1.0,
    val mean2: Double = 0.0,
    val v2: Double = 1.0,
    val corr: Double = 0.0,
    stream: RNStreamIfc = KSLRandom.nextRNStream(),
    name: String? = null
) : MVRVariable(stream, name) {
.
.
.
    override fun generate(array: DoubleArray) {
        require(array.size == dimension) { "The size of the array to fill does not match the sampling dimension!" }
        val z0 = Normal.stdNormalInvCDF(rnStream.randU01())
        val z1 = Normal.stdNormalInvCDF(rnStream.randU01())
        val s1 = sqrt(v1)
        val s2 = sqrt(v2)
        array[0] = mean1 + s1 * z0
        array[1] = mean2 + s2 * (corr * z0 + sqrt(1.0 - corr * corr) * z1)
    }

Figure 8.7 presents the key classes and interfaces involved in the generation of a BVN sample. Notice that the BivariateNormalRV class sub-classes from the MVRVariable class, which in turn implements the MVRVariableIfc and the MVSampleIfc interfaces. The key is the generate(array: DoubleArray) method, in which the generation algorithm must be implemented.

Key Classes for BVN Generation

Figure 8.7: Key Classes for BVN Generation

The functionality of the MVSampleIfc interface is especially noteworthy, with the following methods:

  • sample(): DoubleArray - generates an array that holds the sample
  • sample(array: DoubleArray) - fills the supplied array with the generated values
  • sample(sampleSize: Int): List<DoubleArray> - generates a list holding the randomly generated arrays. This can easily be converted to a 2-dimensional array that contains the samples as its rows.
  • sampleByColumn(sampleSize: Int): Array<DoubleArray> - generates a 2-dimensional array (matrix) where the columns contain the samples.
  • sample(values: Array<DoubleArray>) - fills the supplied array of arrays with randomly generated samples by rows.

The key property is the dimension property, which specifies the size of the array from the sample() method. In the case of the BVN random variable, the dimension is equal to 2. As you can see from Figure 8.7 the analogies with the one dimensional SampleIfc and RVariableIfc interfaces described in Section 2.2 should be clear. In addition, the MVRVariableIfcinterface implements the RNStreamControlIfc and RNStreamChangeIfc interfaces. As you may recall, the RNStreamControlIfc interface allows you to control the underlying stream of random numbers. The multi-dimensional case works the same as in the single variate case. Thus, sampling multi-variate distributions should be a straightforward step as long as you realize that you are generating arrays of data.

There are only two directly implemented bi-variate distributions the bivariate normal and the bivariate lognormal distribution. The implementation of the bivariate lognormal is conceptually similar to that of the bivariate normal. Since it can be shown that for the previously discussed bivariate normal procedure that the generated \(X_1\) and \(X_2\) are individually normally distributed then the algorithm for the generating from the bivariate lognormal distribution is straightforward because of the relationship between the two random variables. That is, if \(X \sim N(\mu, \sigma^2)\) then the random variable \(Y=e^X\) will be lognormally distributed \(LN(\mu_l,\sigma_{l}^{2})\), where

\[ E[Y] = \mu_l = e^{\mu + \sigma^{2}/2} \]

\[ \text{Var}[Y] = \sigma_{l}^{2} = e^{2\mu + \sigma^{2}}\left(e^{\sigma^{2}} - 1\right) \] Thus, in implemented the bivariate lognormal distribution, we just need to generate BVN random variable and apply \(Y=e^X\). This is shown in the generate() method of the BivariateLogNormalRV class.

    override fun generate(array: DoubleArray) {
        require(array.size == dimension) { "The size of the array to fill does not match the sampling dimension!" }
        myBVN.sample(array)
        // transform them to bi-variate lognormal
        array[0] = exp(array[0])
        array[1] = exp(array[1])
    }

Developing your own bivariate generation classes can readily be accomplished by following the pattern presented by the BivariateNormalRV and BivariateLogNormalRV classes and sub-classing from the MVRVariable abstract base class. In this section, we discussed the generation of bivariate normal random variables. The key concept to remember moving into the next section is that now we have a procedure for generating correlated random variables. While the generation of bivariate lognormal random variables used the fact that we can generate bivariate normal random variables, we will see that these ideas can be generalized.

8.3.2 Copulas and Multi-variate Generation Methods

In this section, we will discuss general approaches for generating multi-variate random variables. To reduce the burden of excessive notation, the presentation will focus on the 2-dimensional case. This should not limit the ideas because the concepts can be readily generalized to higher dimensions. One of the most useful concepts used in the generation of multi-variate random variates is that of a copula.

Definition 8.1 (Copula) A d-dimensional copula, \(C : [0,1]^d : \rightarrow [0,1]\) is a cumulative distribution function (CDF) with uniform marginals. That is, if we have a joint distribution of random variables, \((U_1, U_2,\cdots, U_d)\) where each \(U_i \sim U(0,1)\), then the copula is the joint CDF: \[ C(u_1, u_2, \cdots, u_d) = P\{U_1 \leq u_1, U_2 \leq u_2, \cdots, U_d \leq u_d\} \]

Note that in the definition of a copula, the \((U_1, U_2,\cdots, U_d)\) are not assumed to be independent. In fact, the whole point is for them to have a dependence structure. A definitive reference text on copulas, their properties and their uses can be found in (R. B. Nelson 1999). The main theorem concerning copulas that is relevant to our discussion is due to (Sklar 1959), see (R. B. Nelson 1999) for a proof and further discussion.

Theorem 8.1 (Sklar's Theorem) For any random variables, \((X_1, X_2, \cdots, X_d)\) with joint CDF: \[ F(x_1, x_2, \cdots, x_d) = P\{X_1 \leq x_1, X_2 \leq x_2, \cdots, X_d \leq x_d\} \] and marginals \(F_j(x) = P(X_j \leq x_j)\) for \(j=1, 2, \cdots, d\), there exists a copula, such that: \[ F(x_1, x_2, \cdots, x_d) = C(F_1(x_1),F_2(x_2), \cdots, F_d(x_d) ) \] If each \(F_j(x)\) is continuous, then the copula, \(C(\cdot)\) will be unique.

Because of Theorem 8.1, we can express the joint CDF, \(F(\cdot)\) in terms of a copula, \(C(\cdot)\) and a set of marginal distribution functions, \(F_j(x_j)\). This fact allows us to separate the marginals, \(F_j(x_j)\) from the dependence structure implied by the copula, \(C(\cdot)\). This is extremely useful because it allows us to generate dependent \((U_1, U_2,\cdots, U_d)\) and then use the inverse transform technique to generate from each marginal, \(F_j(x_j)\) so that the resulting \(X_j\) have a dependence structure implied by the specified copula.

There are many possible choices for specifying copulas. One way to specify a copula is to extract it from a known joint distribution \(F(\cdot)\) via an inverse transform operation:

\[ C(u_1, u_2, \cdots, u_d) = F(F_1^{-1}(u_1),F_2^{-1}(u_2), \cdots, F_d^{-1}(u_d) ) \] The resulting copula will then take on its name from the joint distribution, \(F\), assuming that the marginals are continuous.

An example of this is the so called Gaussian copula. Let \(\mathbf{X} \sim \text{MVN}_d(\vec{0}, \mathbf{P})\) be a multi-variate normal random variable, where \(\mathbf{P}\) is the correlation matrix of \(\mathbf{X}\). Then, the Gaussian copula is as follows:

\[ C^G_{\mathbf{P}}(u_1, u_2, \cdots, u_d) = \Phi_{\mathbf{P}}(\Phi_1^{-1}(u_1),\Phi_2^{-1}(u_2), \cdots, \Phi_d^{-1}(u_d) ) \] where \(\Phi(\cdot)\) is the standard normal CDF and \(\Phi_{\mathbf{P}}(\cdot)\) is the joint CDF of \(\mathbf{X}\).

To make this concrete, let’s consider the bivariate normal copula. Let \((X_1, X_2)\) be from a bivariate normal distribution such that \(\text{BVN}(\mu_1=0, \sigma^2_1=1,\mu_2 =0, \sigma^2_2 = 1,\rho)\). Now to generate from the Gaussian copula, we have the following algorithm:

  1. Generate \(Z_1 \sim N(0,1)\) and \(Z_2 \sim N(0,1)\)
    1. Generate \(V_1 \sim U(0,1)\) and \(V_2 \sim U(0,1)\)
    2. Let \(z_1 = \Phi^{-1}(v_1)\) and \(z_2 = \Phi^{-1}(v_2)\)
  2. Let \(x_1 = z_1\) and \(x_2 = \rho z_1 + z_2\sqrt{(1-\rho^2)}\).
  3. Let \(u_1 = \Phi(x_1)\) and \(u_2 = \Phi(x_2)\)
  4. Return \((u_1, u_2)\)

The bivariate random variate \((u_1, u_2)\) returned from this algorithm will be from a bivariate Gaussian copula. The random variables from this copula, \((U_1, U_2)\) will be correlated because the generated \((x_1, x_2)\) will have correlation \(\rho\). Thus, we can use the correlated random variables \((U_1, U_2)\) to generate other random variables that have a dependence structure that is implied by the correlation between \((U_1, U_2)\).

For example let \(\vec{Y} = (Y_1, Y_2)\) be a random vector and let \(F_{Y_1}(\cdot)\) and \(F_{Y_2}(\cdot)\) be the marginal distributions associated with \(Y_1\) and \(Y_2\). Then, we can generate \(\vec{Y}\) as follows:

\[ Y_1 = F^{-1}_{Y_1}(u_1) = F^{-1}_{Y_1}(\Phi(x_1))\\ Y_2 = F^{-1}_{Y_2}(u_1) = F^{-1}_{Y_2}(\Phi(x_2))\\ \] where \(x_1 = z_1\) with \(Z_1 \sim N(0,1)\) and \(x_2 = \rho z_1 + z_2\sqrt{(1-\rho^2)}\) with \(Z_2 \sim N(0,1)\). This will cause the vector, \(\vec{Y}\) to have the corresponding Gaussian BVN copula. The KSL BVGaussianCopulaRV class implements these ideas to generate bivariate correlated random variables. The user is required to supply the inverse CDF functions for the two marginals. Note that, in general, the two distributions, \(F_{Y_1}(\cdot)\) and \(F_{Y_2}(\cdot)\) do not have to be from the same family. In addition, as long as the inverse CDF function is available the distribution could be discrete or continuous.

class BVGaussianCopulaRV(
    val marginal1: InverseCDFIfc,
    val marginal2: InverseCDFIfc,
    val bvnCorrelation: Double,
    stream: RNStreamIfc = KSLRandom.nextRNStream()
) : MVRVariable(stream) {

    private val bvGaussianCopula = BVGaussianCopula(bvnCorrelation, stream)

    override val dimension: Int
        get() = bvGaussianCopula.dimension

    override fun generate(array: DoubleArray) {
        require(array.size == dimension) { "The length of the array was not the proper dimension" }
        // generate the uniforms
        val u = bvGaussianCopula.sample()
        // apply the inverse transform for each of the marginals
        array[0] = marginal1.invCDF(u[0])
        array[1] = marginal2.invCDF(u[1])
    }

This idea generalizes to the generation of random vectors of dimension, \(d\), if we use the \(d\)-dimensional Gaussian copula, \(C^G_{\mathbf{P}}(\cdot)\). Thus, because of Sklar’s Theorem the joint distribution of \(\vec{Y}\) can be written using the specified Gaussian copula. This is due to the invariance of copulas to monotonic transformations, which is discussed in (R. B. Nelson 1999).

There are many different kinds of copulas that have been developed which can be used to generate correlated random variables. The general procedure is as follows:

  1. Specify a copula and its parameters
  2. Generate \(\vec{U} = (u_1, u_2,\cdots, u_d)\) from the copula
  3. Generate \(\vec{Y} = (Y_1, Y_2, \cdots, Y_d)\), where \(Y_i = F^{-1}_i(u_i)\)

The generated vector \(\vec{Y}\) will have a dependence structure that is determined by the dependence structure of the vector \(\vec{U}\). It is important to realize that the dependence structures of these two random vectors will be related, but not necessarily the same. The key is to specify a copula that is easy to generate from and to understand how its dependence structure translates to the desired dependence structure. (Nelsen 2004) presents a survey of the properties of various copulas. In addition, a comprehensive compendium of copulas is available in (Nadarajah, Afuecheta, and Chan 2017).

The KSL supports the generation of random vectors due to its implementation of the multi-variate normal distribution. Thus, the Gaussian copula is available to KSL users. In addition, the formulas in (Nadarajah, Afuecheta, and Chan 2017) can be readily implemented for other copulas.

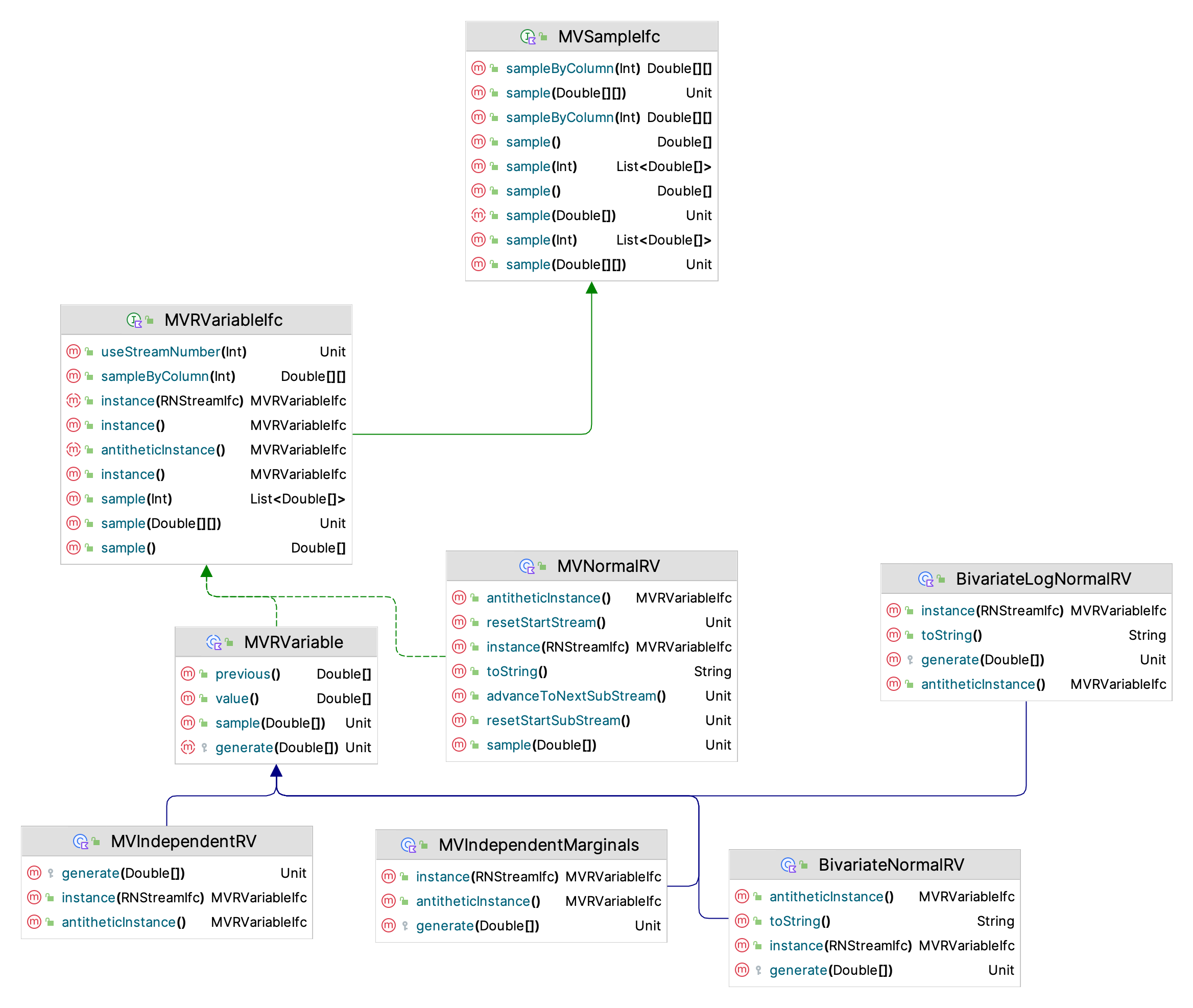
Key Classes for Multi-Variate Generation

Figure 8.8: Key Classes for Multi-Variate Generation

A d-dimensional multi-variate normal distribution is specified by a vector of means \(\vec{\mu} = (\mu_1, \mu_2, \cdots ,\mu_d)^{T}\) and a \(d \times d\) covariance matrix, \(\mathbf{\Sigma}\). The entries of \(\mathbf{\Sigma}\) are \(\text{COV}(X_i, X_j)\) and \(\mathbf{\Sigma}\) is symmetric and positive definite. Define \(\mathbf{C}\) a \(d \times d\) matrix representing the Cholesky decomposition of \(\mathbf{\Sigma}\), where \(\mathbf{\Sigma} =\mathbf{C}\mathbf{C}^{T}\). Then the algorithm for generating MVN random variables is just an extension to the method for generating BVN random variables:

  1. Generate \((Z_1, Z_2, \cdots, Z_d)\) as IID \(N(0,1)\) random variables
  2. For \(i=1,2,\cdots,d\), let \(X_i = \mu_i + \sum_{j=1}^{i}c_{ij}Z_j\), where \(c_ij\) is the \((i,j)\)th element of \(\mathbf{C}\), Return \((X_1, X_2, \cdots, X_d)\)

The KSL MVNormalRV implements this algorithm.

class MVNormalRV constructor(
    means: DoubleArray,
    covariances: Array<DoubleArray>,
    stream: RNStreamIfc = KSLRandom.nextRNStream()
) : MVRVariableIfc

An example for generating from a MVN is shown in the following code.

    val cov = arrayOf(
        doubleArrayOf(1.0, 1.0, 1.0, 1.0, 1.0),
        doubleArrayOf(1.0, 2.0, 2.0, 2.0, 2.0),
        doubleArrayOf(1.0, 2.0, 3.0, 3.0, 3.0),
        doubleArrayOf(1.0, 2.0, 3.0, 4.0, 4.0),
        doubleArrayOf(1.0, 2.0, 3.0, 4.0, 5.0)
    )
    val means = doubleArrayOf(10.0, 10.0, 10.0, 10.0, 10.0)
    val rv = MVNormalRV(means, cov)
    for (i in 1..5) {
        val sample: DoubleArray = rv.sample()
        println(KSLArrays.toCSVString(sample))
    }

This code produces the following output.

10.608312205708812, 12.427876158938025, 15.095818342789086, 13.895399804504395, 15.82457463544744
12.357092448543806, 12.093733136888977, 12.89119464537901, 12.45554505056937, 13.885758234303694
9.351088769471737, 9.08925546297716, 8.826393183582276, 9.972369809797016, 10.15999988875732
9.094163074400619, 8.983286878421879, 10.986502362541005, 10.212432226337382, 11.371691780443308
9.837869522611827, 9.038466912761681, 9.124068606401634, 9.590808967808215, 11.561395573689001

To generate \((U_1, U_2,\cdots, U_d)\) using a Gaussian copula, you can use the MVGaussianCopula class. This class requires the specification of the correlation matrix.

class MVGaussianCopula(
    correlation: Array<DoubleArray>,
    stream: RNStreamIfc = KSLRandom.nextRNStream()
) : MVRVariable(stream){

The following examples illustrates how to use the class.

    val cov = arrayOf(
        doubleArrayOf(1.0, 1.0, 1.0, 1.0, 1.0),
        doubleArrayOf(1.0, 2.0, 2.0, 2.0, 2.0),
        doubleArrayOf(1.0, 2.0, 3.0, 3.0, 3.0),
        doubleArrayOf(1.0, 2.0, 3.0, 4.0, 4.0),
        doubleArrayOf(1.0, 2.0, 3.0, 4.0, 5.0)
    )
    val rho = MVNormalRV.convertToCorrelation(cov)
    val rv = MVGaussianCopula(rho)
    for (i in 1..5) {
        val sample: DoubleArray = rv.sample()
        println(KSLArrays.toCSVString(sample))
    }

This produces the following output, which are all marginal uniform random variables.

0.7285097863655003, 0.9569891872203626, 0.9983698799092053, 0.9742745590896011, 0.9954039933624037
0.9907906696144968, 0.9306291228202694, 0.9524642953735563, 0.8902338139058006, 0.9588737889598452
0.2581978776398398, 0.2597897797244717, 0.24901831402144003, 0.49448874976678453, 0.5285216255173468
0.18251108664042276, 0.2360936451712804, 0.715511037152583, 0.542294556596819, 0.7302070177714262
0.4356015531081042, 0.24828181183321235, 0.3065268847809944, 0.4189440794684452, 0.757498112637931

The MVGaussianCopulaRV class puts all these components together to generate random vectors using the d-dimensional Gaussian copula by allowing the user to specify the inverse CDF functions for the marginal distributions.

class MVGaussianCopulaRV(
    val marginals: List<InverseCDFIfc>,
    correlation: Array<DoubleArray>,
    stream: RNStreamIfc = KSLRandom.nextRNStream()
) : MVRVariable(stream) {

    private val myCopula = MVGaussianCopula(correlation, stream)
.
.
    override fun generate(array: DoubleArray) {
        require(array.size == dimension) { "The length of the array was not the proper dimension" }
        // generate the uniforms
        val u = myCopula.sample()
        // apply the inverse transform for each of the marginals
        for (i in u.indices) {
            array[i] = marginals[i].invCDF(u[i])
        }
    }

Similar strategies can be implemented for other copula specifications.

8.3.3 Autocorrelated Generation

This section involves how to explicitly model dependence (autocorrelation) within random samples. An important application is to generate correlated values from simulation input models. In the fitting of input models, it was assumed and tested that the sample observations did not have correlation. But, what do you do if the data does have correlation? For example, let \(X_i\) be the service time of the \(i^{th}\) customer. What if the \(X_i\) have significant correlation? That is, the service times are correlated. Input processes might also correlated. That is, the time between arrivals might be correlated. Research has shown, see see (Patuwo, Disney, and Mcnickle 1993) and (Livny, Melamed, and Tsiolis 1993), that ignoring the correlation when it is in fact present can lead to gross underestimation of the actual performance estimates for the system.

The discussion here is based on the Normal-to-Anything Transformation as discussed in Banks et al. (2005), (Cario and Nelson 1998), (Cario and Nelson 1996), and (Biller and Nelson 2003). Suppose you have a \(N(0,1)\) random variable, \(Z_i\), and a way to compute the CDF, \(\Phi(z)\), of the normal distribution. Then, from the discussion of the inverse transform technique, the random variable, \(\Phi(Z_i)\) will have a U(0,1) distribution. Suppose that you wanted to generate a random variable \(X_i\) with CDF \(F(x)\), then you can use \(\Phi(Z_i)\) as the source of uniform random numbers in an inverse transform technique.

\[ X_i = F^{-1}(U_i) = F^{-1}((\Phi(Z_i))) \] This transform is called the normal-to-anything (NORTA) transformation. It can be shown that even if the \(Z_i\) are correlated (and thus so are the \(\Phi(Z_i)\) then the \(X_i\) will have the correct CDF and will also be correlated. Unfortunately, the correlation is not directly preserved in the transformation so that if the \(Z_i\) has correlation \(\rho_z\) the \(X_i\) will have \(\rho_x\) (not necessarily the same). Thus, in order to induce correlation in the \(X_i\) you must have a method to induce correlation in the \(Z_i\).

One method to induce correlation in the \(Z_i\) is to generate the \(Z_i\) from an stationary autoregressive time-series model of order 1, i.e. \(AR(1)\). A stationary \(AR(1)\) model with \(N(0,1)\) marginal distributions has the following form:

\[ Z_i = \phi(Z_{i-1}) + \varepsilon_i \]

where \(i = 1,2,3,\ldots\) and \(\varepsilon_i\) are IID \(N(0,1-\phi^2)\), \(i = 1,2,3,\ldots\), \(-1<\phi<1\), and \(Z_1 \sim N(0,1)\). Thus, it is relatively straightforward to generate this process by first generating \(Z_1\), then generating \(\varepsilon_i \sim N(0,1-\phi^2)\) and using \(Z_i = \phi(Z_{i-1}) + \varepsilon_i\) to compute the next \(Z_i\). It can be shown that this \(AR(1)\) process will have lag-1 correlation:

\[ \phi = \rho^1 = corr(Z_i, Z_{i+1}) \] Therefore, you can generate a random variable \(Z_i\) that has a desired correlation and through the NORTA transformation produce \(X_i\) that are correlated with the correlation being functionally related to \(\rho_z\). By changing \(\phi\) through trial and error one can get the correlation for the \(X_i\) that is desired. Procedures for accomplishing this are given in the previously mentioned references.

The implementation of this technique can be readily achieved in a general way within the KSL through the use of the AR1NormalRV class and already available constructs. The AR1CorrelatedRNStream class implements these ideas in the form of a stream that can be supplied to random variables and other constructs that require a stream.

class AR1CorrelatedRNStream(
    lag1Corr: Double,
    stream: RNStreamIfc = KSLRandom.nextRNStream(),
) : RNStreamIfc by stream {

    private val myAR1NormalRV = AR1NormalRV(lag1Corr = lag1Corr, stream = stream)
    private var myPrevU : Double = Double.NaN

    val ar1LagCorr
        get() = myAR1NormalRV.lag1Corr

    override val previousU: Double
        get() = myPrevU

    override fun randU01(): Double {
        val z = myAR1NormalRV.value
        val u = Normal.stdNormalCDF(z)
        myPrevU = u
        return u
    }
}

The AR1CorrelatedRNStream class overrides the randU01() method to implement the ARTA concept. To use this class just supply it as the stream for the random variable.

val e = ExponentialRV(mean=10.0, stream = AR1CorrelatedRNStream(lag1Corr = 0.85))

In the next section, we explore a general method for generating multi-variate samples using Markov Chain Monte Carlo methods.

8.3.4 Introduction to Markov Chain Monte Carlo Methods

In this section, we present the a brief overview of Markov Chain Monte Carlo (MCMC) methods, especially as they relate to the constructs available within the KSL. MCMC has a deep and important history of both theoretical and practical applications. This overview provides a minimal amount of theory and then presents the related KSL classes. For tutorials on MCMC the reader should consult the following references, (Brooks 1998), (Robert and Changye, n.d.), (Geyer 2011), (Van Ravenzwaaij and Brown 2018), and (Speagle 2020). For textbook treatments within the context of simulation, the reader might consult (S. M. Ross 2023), (G. Fishman 2006), or (Rubinstein and Kroese. 2017).

MCMC is a numerical simulation technique that facilitates the approximate generation of random variates from arbitrary distributions. The distributions need only be specified up to a multiplicative constant, which is very useful in Bayesian applications. In addition, the theory works for multi-variate distributions, which allows for the generation of random vectors from arbitrary joint probability distributions. Because MCMC facilitates the generation of samples from multi-variate distributions it often has applications in estimating complex multi-dimensional integrals and has applications in the optimization of multi-variate functions.

Recall that the application of the Monte Carlo method, basically comes down to solving problems of the form for \(\vec{x} \in \mathbb{R}^d\) and integration limit set, \(S\), such that \(S \subseteq \mathbb{R}^d\):

\[ \theta = \int\limits_S g(\vec{x}) \mathrm{d}\vec{x} \]

We estimated \(\theta\) by generating random samples of \(\vec{X}_i\) according to some probability distribution \(w(\vec{x})\) over the limiting set, \(S\), and averaging over the \(Y_i\), where

\[ Y_i = \frac{g(\vec{X}_i)}{w(\vec{X}_i)} \]

which is justified because

\[ E[Y] = E_{\vec{X}}\bigg[\frac{g(\vec{X})}{w(\vec{X})}\bigg]=\int\limits_{S} g(\vec{x}) \mathrm{d}\vec{x} =\theta \]

When we discussed importance sampling, we noted that \(g(\vec{x})\) can be factorized as follows \(g(\vec{x}) = h(\vec{x})w(\vec{x})\) where \(w(\vec{x})\) is a probability distribution with \(\vec{x} \in S \subseteq \mathbb{R}^d\). Thus, an estimate of \(\theta\) is

\[ \hat{\theta} = \bar{Y}(n) = \frac{1}{n}\sum_{i=1}^{n}Y_i=\frac{1}{n}\sum_{i=1}^{n}\frac{g(\vec{X}_i)}{w(\vec{X}_i)}=\frac{1}{n}\sum_{i=1}^{n}h(\vec{X}_i) \]

We know that independent \(\vec{X}_i\) ensures that the law of large numbers has, \(\hat{\theta} \rightarrow \theta\) as \(n \rightarrow \infty\) with probability 1. But what happens if the \(\vec{X}_i\) are dependent? Under some technical conditions, it can still be shown that \(\hat{\theta} \rightarrow \theta\). Thus, sequences of dependent \(\vec{X}_i\) could be used. One method for generating depended \(\vec{X}_i\) would be from a Markov chain that has \(w(\vec{X})\) as its stationary limiting distribution. In the Markov Chain literature, \(w(\vec{X})\) is often denoted as \(\pi(\vec{X})\).

For simplicity in what follows, we will focus on the univariate case, with the understanding that the presentation can be extended to a multi-dimensional setting. Because it should make it easier to conceptualize the approach, we will first present some basic concepts using discrete Markov Chains.

A Markov Chain is a collection of random variables \(\{X_1,X_2,\cdots\}\) where we interpret the \(X_n\) as the state of the process at time step \(n\). For simplicity, suppose the state space is finite and labeled \(\{1,2,\cdots,N\}\). Let \(P\{X_{n+1} =j | X_n =i, X_{n-1} =k, \cdots,X_0 = l \}\) be the probability that the process transitions to state \(j\) at time \(n+1\) given all previous state visits. If this probability only depends on the previous state, then we have a Markov Chain. Thus, if the following is true

\[ P\{X_{n+1} =j | X_n =i, X_{n-1} =k, \cdots,X_0 = l \} = P\{X_{n+1} =j | X_n =i\} \] We call \(P\{X_{n+1} =j | X_n =i\}\) the single step transition probabilities, \(p_{ij}\), and the process \(\{X_n\}\) is a Markov Chain. Notice that the \(p_{ij}\) form a conditional probability distribution across the states \(j=1, 2,\cdots, N\) for a given state \(i\). Thus, we have that

\[ \sum_{j=1}^N p_{ij}= \sum_{j=1}^NP\{X_{n+1} =j | X_n =i\}=1 \] Therefore the process must be in some state \(j \in \{1,2,\cdots,N\}\) after it transitions from state \(i\). To simulate \(k\) transitions of a discrete state Markov Chain, we can perform the following algorithm:

  1. initialize \(X_0=i\) and \(n=0\)

for n = 1 to k;

  1. generate \(j \sim P\{X_{n+1}| X_n =i\}\)
  2. let \(X_n = j\) and \(i=j\)

end for;

The KSL DMarkovChain class in the ksl.utilities.random.markovchain package facilitates the simulation of simple discrete state Markov Chains.

Example 8.7 (Simulating a Markov Chain) An ergodic Markov Chain is setup and simulated with statistics collected on the probability of being within the states.

    val p = arrayOf(
        doubleArrayOf(0.3, 0.1, 0.6),
        doubleArrayOf(0.4, 0.4, 0.2),
        doubleArrayOf(0.1, 0.7, 0.2)
    )

    val mc = DMarkovChain(1, p)
    val f = IntegerFrequency()

    for (i in 1..100000) {
        f.collect(mc.nextState())
    }
    println("True Steady State Distribution")
    println("P{X=1} = " + 238.0 / 854.0)
    println("P{X=2} = " + 350.0 / 854.0)
    println("P{X=3} = " + 266.0 / 854.0)
    println()
    println("Observed Steady State Distribution")
    println(f)

This code results in the following output.

True Steady State Distribution
P{X=1} = 0.2786885245901639
P{X=2} = 0.4098360655737705
P{X=3} = 0.3114754098360656

Observed Steady State Distribution
Frequency Tabulation ID_2
----------------------------------------
Number of cells = 3
Lower limit = -2147483648
Upper limit = 2147483647
Under flow count = 0
Over flow count = 0
Total count = 100000.0
Minimum value observed = 1
Maximum value observed = 3
----------------------------------------
Value    Count   Proportion
1    27812.0     0.27812
2    41138.0     0.41138
3    31050.0     0.3105
----------------------------------------

As we can see from the output, the distribution of the observations from the chain are converging to the steady state limiting distribution.

There are many issues related to the analysis of Markov Chains that are discussed in some of the aforementioned textbooks. The main property of concern here is that a Markov Chain is said to be irreducible if for each pair of states \(i\) and \(j\), there exists a probability of starting in state \(i\) that eventually allows state \(j\) to be visited. For an irreducible Markov Chain that is also aperiodic, there will exist a limiting distribution across the states, \(\pi_j = \underset{n \rightarrow \infty}{\text{lim}}P\{X_n = j\}\), which represents the steady state probability that the process is in state \(j\) or sometimes called the long run proportion of time that the process is in state \(j\). Suppose now that we have a Markov Chain such that \(\pi_j\) exists, then it can be shown that for any function \(h(\cdot)\) on \(X_n\), that:

\[ \underset{n \rightarrow \infty}{\text{lim}}\frac{1}{n}\sum_{i=1}^{n}h(X_i)=\sum_{j=1}^{N}h(j)\pi_j \quad \text{w.p.} \, 1 \] This result is the motivation for MCMC.

In MCMC, we want to generate random variables, \(X \sim P(X=j)\), for \(j=1,2,\cdots,N\) and estimate \(E[h(X)]= \sum_{j=1}^{N}h(j)p_j\). Thus, why not set up a Markov Chain with limiting probability \(\pi_j = p_j\), then \(X_n\) will have approximately the distribution of \(X\) after a sufficiently large number of steps \(n\) of the Markov Chain. Thus, we can estimate \(E[h(X)]\) by \(\frac{1}{n}\sum_{i=1}^{n}h(X_i)\) for large \(n\). The key requirement is to be able to set up a Markov Chain such that \(\pi_j = p_j\) is true. You might ask, if we have \(p_j\), why not just use:

\[ E[h(X)] =\sum_{j=1}^{N}h(j)p_j \] In many cases, especially in the continuous case, \(p_j\) is not known or is known only up to a multiplicative constant. This is when MCMC become useful. In traditional Markov Chain theory, we are typically interested in determining the steady state distribution, \(\pi_j\) from a given transition matrix, \(\mathbf{P}\), assuming that it is irreducible and aperiodic. The key MCMC result, turns this problem around: Given a desired \(\pi_j\) what \(\mathbf{P}\) should we construct to get the desired \(\pi_j\). The Metropolis-Hastings algorithm prescribes a method to address this problem.

The basic idea behind the Metropolis-Hastings algorithm is to use an arbitrary transition matrix \(\mathbf{Q}\) and accept or reject proposed state changes in such a manner that the resulting observations will come from a transition matrix \(\mathbf{P}\) that has the desired \(\pi_j\). The steps are as follows:

  1. When \(X_n = i\), generate random variable \(Y \sim P(Y=j) = q_{ij}\), \(j \in S\)
  2. If \(Y=j\), let \(X_{n+1} = j\) with probability \(\alpha_{ij}\) or \(i\) with probability \(1-\alpha_{ij}\), where \(\alpha_{ij} = min\bigg[\frac{\pi_jq_{ji}}{\pi_iq_{ij}},1\bigg]\)

The resulting Markov Chain, \(X_n\) will have one step transition probabilities:

\[ p_{ij}= \begin{cases} q_{ij}\alpha_{ij} & \text{if} \, i \ne j\\ 1 - \sum_{k\ne i}q_{ik}\alpha_{ik} & \text{if} \, i = j \end{cases} \] and the Markov Chain will have the desired stationary probabilities \(\pi_j\). The proof of this result can be found in (S. M. Ross 2023). This seems like a lot of work given that we have to know \(\pi_j\); however, close examination of \(\alpha_{ij}\) indicates that we need only know \(\pi_j\) up to proportionality constant, e.g. \(\pi_j = b_i/C\) because of the ratio form of \(\alpha_{ij}\).

The payoff is when we want to generate samples from some arbitrary multi-dimensional pdf, \(f(\vec{x})\). The theory can be generalized to this case by generalizing from a discrete Markov Chain to a continuous Markov Chain. This is done by defining a probability transition function \(q(\vec{x},\vec{y})\) which is called the proposal function. The proposal function proposes the next state and is acting as the arbitrary transition matrix \(\mathbf{Q}\). With that in mind, it is really a conditional probability density function \(q(\vec{y}|\vec{x})\) which represents the probability of generating \(\vec{Y}\) given we are in state \(\vec{x}\). The \(\alpha_{ij}\) is generalized to a function, \(\alpha(\vec{x},\vec{y})\), which is called the acceptance probability function. The general Metropolis-Hastings algorithm is:

Let \(f(\vec{x})\) be the target distribution.

Let \(q(\vec{y}|\vec{x})\) be the proposal distribution.

Let \(\rho(\vec{x},\vec{y})\) be the acceptance ratio, where

\[ \rho(\vec{x},\vec{y}) = \frac{ q(\vec{x}|\vec{y})\times f(\vec{y})}{ q(\vec{y}|\vec{x}) \times f(\vec{x})} \] Let \(\alpha(\vec{x},\vec{y}) = min[\rho(\vec{x},\vec{y}),1 ]\) be the acceptance function.

  1. Set \(t=0\)
  2. Set \(X_0\)

for t = 1 to ?;

  1. \(Y \sim q(\vec{y}|\vec{x})\)
  2. \(U \sim U(0,1)\)
  3. if \(U \leq \alpha(\vec{x},\vec{y})\) then \(X_{t+1} = Y\) else \(X_{t+1} = X_t\)

end for;

When applying the Metropolis-Hastings algorithm, you obviously need the distribution from which you intend to generate random variates, \(f(\vec{x})\). The function \(f(\vec{x})\) can be the distribution function specified up to a proportionality constant. The second key function is the proposal distribution (or proposal function), \(q(\vec{x},\vec{y}) = q(\vec{y}|\vec{x})\). There are many possible forms for this function and those forms specify the type of sampler for the MCMC.

Figure 8.9 presents the main classes and interfaces for the Metropolis-Hastings implementation within the KSL. The MetropolisHastingsMV class is supported by two interfaces: 1) FunctionMVIfc and 2) ProposalFunctionMVIfc.. Let’s examine these two classes before reviewing the the Metropolis-Hastings implementation.

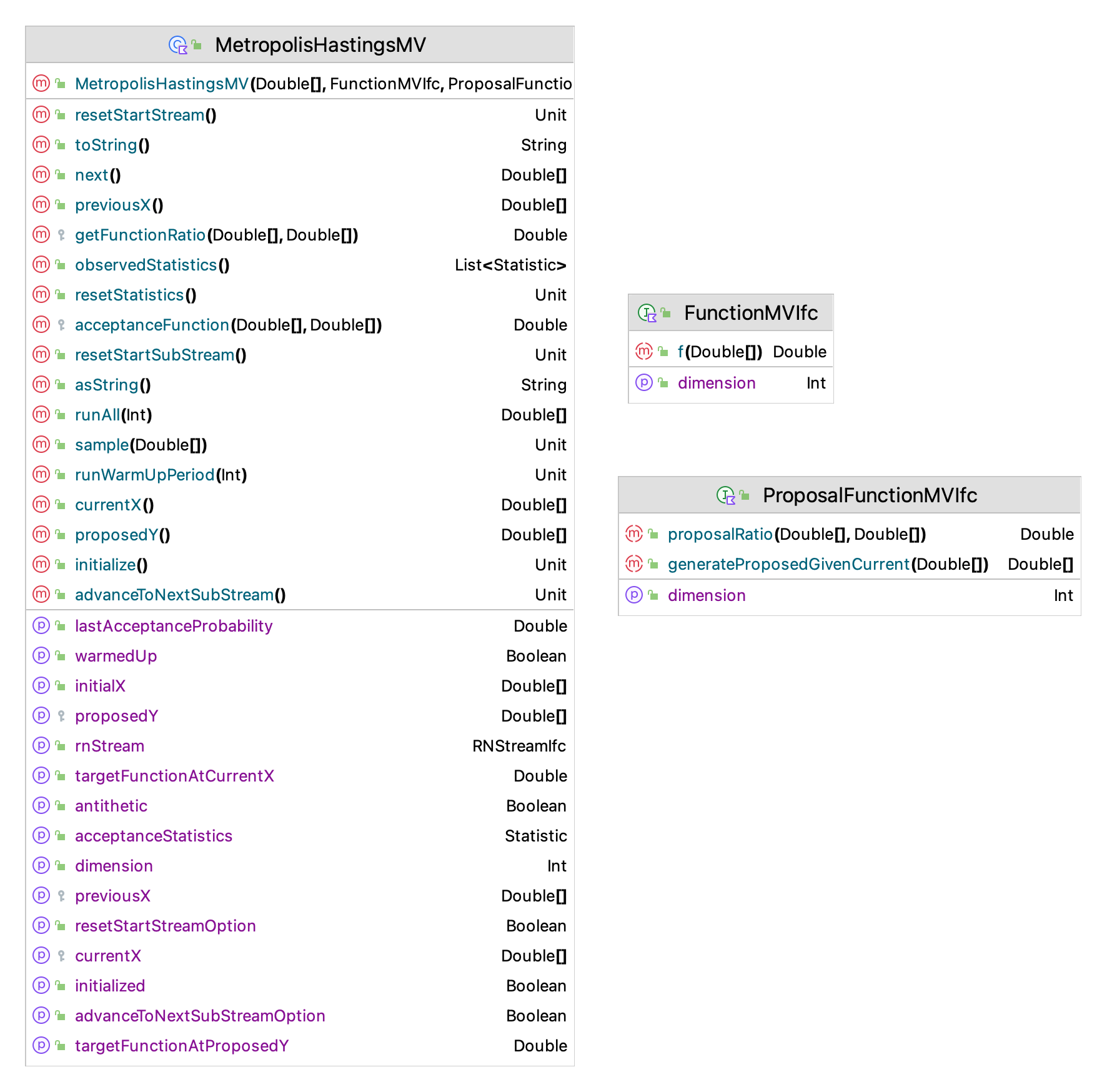
Key Classes and Interfaces for MCMC

Figure 8.9: Key Classes and Interfaces for MCMC

The purpose of the FunctionMVIfc interface is to represent the desired multi-variate distribution, \(f(\vec{x})\). This is the probability density of the distribution from which you want the random vectors. This interface requires the dimension of the function and the method to represent the functional transformation.

interface FunctionMVIfc {

    /**
     *
     * the expected size of the array
     */
    val dimension: Int

    /**
     * Returns the value of the function for the specified variable value.
     * The implementor of f(x) should check if the array size is the
     * same as the dimension of the function
     */
    fun f(x: DoubleArray): Double
}

The second interface is the ProposalFunctionMVIfc interface which represents proposal density function \(q(\vec{y}|\vec{x})\) with the generateProposedGivenCurrent() function and the proposal function’s contribution to the computation of the acceptance ratio function, \(\rho(\vec{x},\vec{y})\) via the proposalRatio() function. The examples that follow will illustrate this function. The generateProposedGivenCurrent() function takes in the current state as its parameter and returns a possible next state.

interface ProposalFunctionMVIfc {

    /**
     *
     * the expected size of the array
     */
    val dimension: Int

    /** The ratio of g(y,x)/g(x,y).  The ratio of the proposal function
     * evaluated at x = current and y = proposed, where g() is some
     * proposal function of x and y. The implementor should ensure
     * that the returned ratio is a valid double
     *
     * @param current the x to evaluate
     * @param proposed the y to evaluate
     * @return the ratio of the proposal function
     */
    fun proposalRatio(current: DoubleArray, proposed: DoubleArray): Double

    /**
     *
     * @param current the current state value of the chain (i.e. x)
     * @return the generated possible state (i.e. y) which may or may not be accepted
     */
    fun generateProposedGivenCurrent(current: DoubleArray): DoubleArray
}

Let’s consider a couple of common samplers. The first to consider is the independence sampler. For the independence sampler, the probability of going to \(\vec{y}\) from state \(\vec{x}\) is independent of \(\vec{x}\). Thus, the proposal function, \(q(\vec{y}|\vec{x})\) is simply a function of \(\vec{y}\). That is, \(q(\vec{y}|\vec{x}) = q(\vec{y})\). This causes the acceptance ratio to be:

\[ \rho(\vec{x},\vec{y}) = \frac{ q(\vec{x}|\vec{y})\times f(\vec{y})}{ q(\vec{y}|\vec{x}) \times f(\vec{x})} = \frac{ q(\vec{x})\times f(\vec{y})}{ q(\vec{y}) \times f(\vec{x})} \] Similar in some respects as the acceptance-rejection method, good proposal functions \(q(\vec{y})\) should have similar shape as \(f(\vec{x})\). Even though the name of this sampler suggests independence, this independence is in the proposal function, not in the resulting Markov Chain and its state values. That is, the generated \(\vec{X}_i\) will be dependent because they come from the underlying Markov Chain implied by the proposal function.

Another common sampler is the random walk sampler. For a random walk sampler, the proposal function is symmetric. Because of symmetry, \(q(\vec{y}|\vec{x}) = q(\vec{x}|\vec{y})\). This causes the acceptance ratio to be:

\[ \rho(\vec{x},\vec{y}) = \frac{ q(\vec{x}|\vec{y})\times f(\vec{y})}{ q(\vec{y}|\vec{x}) \times f(\vec{x})} = \frac{f(\vec{y})}{f(\vec{x})} \] Typical implementations have, \(\vec{Y} = \vec{x} + \vec{W}\), where \(\vec{W} \sim G(\vec{W})\) and the distribution \(G(\cdot)\) is symmetric, such as the multi-variate normal distribution, \(\textbf{MVN}(\vec{0}, \mathbf{\Sigma})\). Let’s look at an example to put these ideas into practice.

Example 8.8 (MCMC Sampler Example) Suppose that the random variable \(X_1\) is the zinc content of an ore sample with a range of values in \([0.5, 1.5]\) and the random variable \(X_2\) is the iron content of the ore with values in \([20.0, 35.0]\). The joint distribution density function for the random variables has been modeled as:

\[ f(x_1, x_2) = \begin{cases} \frac{39}{400} - \frac{17(x_1 - 1)^2}{50} - \frac{(x_2 - 25)^2}{10000} & \, 0.5 \leq x_1 \leq 1.5; \, 20 \leq x_2 \leq 35\\ 0.0 & otherwise \end{cases} \]

  1. Develop a MCMC independent sampler to generate \((X_1, X_2)\) from this distribution.
  2. Develop a MCMC random walk sampler to generate \((X_1, X_2)\) from this distribution.

The key issue is developing a suitable proposal function. Recall that for an independence sampler, we have \(q(\vec{y}|\vec{x}) = q(\vec{y})\). The function, \(q(\vec{y})\) is a probability density function and it must be a function of \(\vec{y} = (y_1, y_2)^T\). That is, \(q(y_1, y_2)\) is a joint density function for random variables \(Y_1\) and \(Y_2\). Now, it might be more readily apparent as to the reason an independence sampler is common. Notice that the general proposal function \(q(\vec{y}|\vec{x})\) would be a conditional distribution of the form \(q(y_1,y_2|X_1=x_1,X_2=x_2)\). Thus, an independence sampler avoids having to develop a function that includes \(X_1=x_1,X_2=x_2\) in its functional form. So, we need a joint density function that will generate, \((Y_1, Y_2)\).

The proposed random vector, \(\vec{Y}\), needs to be within the set of possible values for \(\vec{X}\). There is no requirement that the joint density have a correlation structure. Thus, it is acceptable to specify the distributions for \(Y_1\) and \(Y_2\) as independent marginals. Therefore to keep things simple for illustrative purposes, we will specify \(Y_1 \sim beta(\alpha_1 = 2, \alpha_2=5, min = 0.5, max=1.5)\) and \(Y_2 \sim beta(\alpha_1 = 2, \alpha_2=5, min = 20.0, max=35.0)\). Both of these distributions are not symmetric and cover the ranges for \(Y_1\) and \(Y_2\).

We make no claim that these distributions are better than any other distributions for the range of \(\vec{X}\) for the purposes of MCMC. They simply meet the requirement. Thus, letting \(g_{Y_1}(y_1)\) be the generalized beta PDF for \(Y_1\) and \(g_{Y_2}(y_2)\) be the generalized beta PDF for \(Y_2\), we have that the joint density \(q(y_1, y_2) = g_{Y_1}(y_1) \times g_{Y_2}(y_2)\) because of the assumption of independence between \(Y_1\) and \(Y_2\).

Now we can specify the acceptance ratio function:

\[ \rho(\vec{x},\vec{y}) = \frac{ q(\vec{x}|\vec{y})\times f(\vec{y})}{ q(\vec{y}|\vec{x}) \times f(\vec{x})} = \frac{ q(\vec{x})\times f(\vec{y})}{ q(\vec{y}) \times f(\vec{x})} = \frac{ g_{Y_1}(x_1) \times g_{Y_2}(x_2)\times f(y_1, y_2)}{ g_{Y_1}(y_1) \times g_{Y_2}(y_2) \times f(x_1, x_2)} \] Notice that \(\rho(\vec{x},\vec{y})\) is simply a function of \(x_1,x_2,y_1,y_2\). We are evaluating the probability density functions at the points \(x_1,x_2,y_1,y_2\). Thus, \(\rho(\vec{x},\vec{y})\) is essentially a likelihood ratio. In implementing the Metropolis-Hastings algorithm it is useful to define the acceptance ratio, \(\rho(\vec{x},\vec{y})\), in terms of the proposal ratio, \(p_r(\vec{x},\vec{y})\), and the function ratio, \(f_r(\vec{x},\vec{y})\), where:

\[ p_r(\vec{x},\vec{y}) = \frac{ q(\vec{x}|\vec{y})}{ q(\vec{y}|\vec{x})} \] and,

\[ f_r(\vec{x},\vec{y}) = \frac{ f(\vec{y})}{f(\vec{x})} \] which yields, \(\rho(\vec{x},\vec{y}) = p_r(\vec{x},\vec{y}) \times f_r(\vec{x},\vec{y})\). The proposalRatio() function of the ProposalFunctionMVIfc interface implements \(p_r(\vec{x},\vec{y})\).

To implement the Metropolis-Hastings algorithm for this sampler we need to implement the FunctionMVIfc interface to implement the distribution of interest. Here is the KSL code for the example problem.

object Function : FunctionMVIfc {
    override val dimension: Int
        get() = 2

    override fun f(x: DoubleArray): Double {
        val x0p = 17.0 * (x[0] - 1.0) * (x[0] - 1.0) / 50.0
        val x1p = (x[1] - 25.0) * (x[1] - 25.0) / 10000.0
        return (39.0 / 400.0) - x0p - x1p
    }
}

In addition, we need to implement the ProposalFunctionMVIfc interface, which requires the proposal ratio, \(p_r(\vec{x},\vec{y})\) and the proposal function \(q(\vec{x}|\vec{y})\). The KSL code for the suggested independence sampler is as follows. The code used the GeneralizedBeta class from the ksl.utilities.distributions package because the distributions package contains the implementations for the probability density function.

object ExampleIndependencePF : ProposalFunctionMVIfc {

    private val myY1Dist = GeneralizedBeta(alphaShape = 2.0, betaShape = 5.0, minimum = 0.5, maximum = 1.5)
    private val myY2Dist = GeneralizedBeta(alphaShape = 2.0, betaShape = 5.0, minimum = 20.0, maximum = 35.0)
    private val myY1RV = myY1Dist.randomVariable
    private val myY2RV = myY2Dist.randomVariable

    override val dimension: Int
        get() = 2

    override fun proposalRatio(currentX: DoubleArray, proposedY: DoubleArray): Double {
        //g(y|x) = g(x,y)
        // proposal ratio = g(x|y)/g(y|x) = g(y,x)/g(x,y)
        // for independent sampler the proposal ratio is g(x)/g(y)
        val gx = myY1Dist.pdf(currentX[0]) * myY2Dist.pdf(currentX[1])
        val gy = myY1Dist.pdf(proposedY[0]) * myY2Dist.pdf(proposedY[1])
        return (gx / gy)
    }

    override fun generateProposedGivenCurrent(currentX: DoubleArray): DoubleArray {
        return doubleArrayOf(myY1RV.value, myY2RV.value)
    }
}

To run the simulation and generate the random vectors, we use the MetropolisHastingsMV class as illustrated in the following code. Because the function in the example is relatively simple, the expected values of the marginals can be readily computed. In this case, \(E[X_1] = 1.0\) and \(E[X_2] = 27.5\), which were used as the initial state of the chain. The initial starting point can be some arbitrary state as long as it is a legal. This code warms the chain up by 10000 steps and attaches an observer to the generation process to capture the generated values to a file.

    val f = Function
    val q = ExampleIndependencePF
    val x0 = doubleArrayOf(1.0, 27.5)
    val m = MetropolisHastingsMV(x0, f, q)
    m.runWarmUpPeriod(10000)
    m.attachObserver(WriteData("IndData.csv"))
    m.runAll(10000)
    println(m)

The results are only illustrative of the type of default results that are available.

MetropolisHastings1D
Initialized Flag = true
Burn In Flag = true
Initial X =[0.9594860880833775, 28.12096270621112]
Current X = [0.906954110208565, 26.987110000370624]
Previous X = [1.1256323226794631, 30.436063687178418]
Last Proposed Y= [0.906954110208565, 26.987110000370624]
Last Prob. of Acceptance = 0.04051986694353263
Last f(Y) = 0.09416157659823556
Last f(X) = 0.08917853778826954
Acceptance Statistics
Statistic{name='Acceptance Statistics', n=10000.0, avg=0.3430999999999989, sd=0.4747682913728006, ci=[0.3337935942370735, 0.3524064057629243]}
BatchStatistic{name='X_1', n=39.0, avg=0.9967017932134693, sd=0.15875667093683876, ci=[0.9452388337522397, 1.0481647526746989], lag-1 corr=0.496713378422824, Total number observed = 10000.0}
BatchStatistic{name='X_2', n=39.0, avg=26.081192452184705, sd=1.3778407004302573, ci=[25.63454816510158, 26.52783673926783], lag-1 corr=0.23746016384798618, Total number observed = 10000.0}

The MetropolisHastingsMV class automatically estimates the probability of acceptance for the generation process. Generally, the higher the better for efficiency and other characteristics of the chain. In general, achieving a high probability of acceptance may be quite difficult. Probability of acceptance values in the range from 20-50% are not uncommon. Notice that the statistics collected on the marginal output are close to what is expected. The default results use the BatchStatistic class because of the correlation that is typically present in MCMC output. The correlation reported is for the batch means, not the state observations. The raw observation statistics based on the Statistic class can be obtained via the observedStatistics() method of the MetropolisHastingsMV class. Keep in mind that the confidence intervals reported from the Statistic class assume independent observations. Thus, they will have bias as discussed in Section 5.6.3.

We can see from some of the initial data that the state vector can repeat in the sampling. Large lengths of runs for repeated observations indicates that the Markov Chain is not mixing very well. This can be a common occurrence for independence samplers. We leave it as an exercise for the reader to improve the sampling.

0.6351363119853689, 26.352266492202997
0.5982875748975195, 23.90232944372732
0.6190352791846846, 21.02435324965421
0.9193784433785976, 21.682499716304555
0.9193784433785976, 21.682499716304555
0.9193784433785976, 21.682499716304555
0.931177812433096, 24.40013423216797
0.931177812433096, 24.40013423216797
0.931177812433096, 24.40013423216797
0.931177812433096, 24.40013423216797
0.931177812433096, 24.40013423216797
0.5712462807702627, 30.282898990787338

We will reexamine the example, in order to illustrate a random walk sampler. For a random walk sampler, we need to have a symmetric distribution. The random variable \(X\) has a symmetric distribution if and only if there is a number \(c\) such that \(P(X < c − k)=P(X > c+k)\), for all \(k\). A partial list of symmetric distributions can be found on this Wikipedia page. The most commonly used distributions in random walk samplers are the uniform and the normal distributions.

The main challenge that we face in this example is that the proposal distribution, \(q(\vec{x}|\vec{y})\) should have the same set of possible values as the multi-variate distribution function \(f(\vec{x})\). In the example \(f(\vec{x})\) is bounded within the limits, \(0.5 \leq x_1 \leq 1.5\) and \(20 \leq x_2 \leq 35\). We avoided this issue in the independence sampler implementation because of the choice of the beta distributions for the marginals of the sampler.

As previously noted, typical implementations have, \(\vec{Y} = \vec{x} + \vec{W}\), where \(\vec{W} \sim G(\vec{W})\) and \(G(\cdot)\) is symmetric. Because the proposed value \(\vec{x} + \vec{W}\) may “walk” outside the bounds, we need to handle this situation. One possible choice would be to use the truncated normal distribution \(N_{[a,b]}(\mu = x, \sigma^2)\), where \([a,b]\) is specified by our limits on \(\vec{X}\). We leave this possibility as an exercise for the reader. In this example, we will use the uniform distribution \(U(x-c,x+c)\) where \(c > 0\) is some typically small positive constant. We will handle the boundary situation within the implementation.

The implementation for \(f(\vec{x})\) remains the same. The proposal ratio and proposal function are implemented in the following code. Here we specify the intervals for each of the dimensions, the small constants, \(c_i\) for each dimension, and the random variable, \(e_i \sim U(-c_i, c_i)\) for each dimension. In this case the proposal ratio is always 1.0.

object ExampleRandomWalkPF : ProposalFunctionMVIfc {
    private val y1Interval = Interval(0.5, 1.5)
    private val y2Interval = Interval(20.0, 35.0)
    private val y1c = 1.0
    private val y2c = 5.0
    private val e1rv = UniformRV(-y1c, y1c)
    private val e2rv = UniformRV(-y2c, y2c)

    override val dimension: Int
        get() = 2

    override fun proposalRatio(currentX: DoubleArray, proposedY: DoubleArray): Double {
        //g(y|x) = g(x|y) proposal ratio = g(x|y)/g(y|x) = 1.0
        return (1.0)
    }

    private fun genYGivenX(interval: Interval, rv: UniformRV, x: Double): Double {
        var yp: Double
        do {
            val e = rv.value
            yp = x + e
        } while (!interval.contains(yp))
        return yp
    }
    
    override fun generateProposedGivenCurrent(currentX: DoubleArray): DoubleArray {
        val y1 = genYGivenX(y1Interval, e1rv, currentX[0])
        val y2 = genYGivenX(y2Interval, e2rv, currentX[1])
        return doubleArrayOf(y1, y2)
    }
}

A small private function genYGivenX() is used to sample a value \(x_i + e_i\) until the values are within the desired intervals. To setup and run this case, we have the following code, which is similar to previous run simulation code, except for the use of the random walk sampler.

    val f = Function
    val q = ExampleRandomWalkPF
    val x0 = doubleArrayOf(1.0, 27.5)
    val m = MetropolisHastingsMV(x0, f, q)
    m.runWarmUpPeriod(10000)
    m.attachObserver(WriteData("RWData.csv"))
    m.runAll(10000)
    println(m)

The results could be considered a bit better than the independence sampler results. Clearly, the acceptance probability is significantly better for this sampler.

MetropolisHastings1D
Initialized Flag = true
Burn In Flag = true
Initial X =[0.773680150259463, 25.06436933842605]
Current X = [1.393917079069964, 20.76389519938342]
Previous X = [1.1538567477857675, 25.59456469111667]
Last Proposed Y= [1.393917079069964, 20.76389519938342]
Last Prob. of Acceptance = 0.48031020870117797
Last f(Y) = 0.04294751544959516
Last f(X) = 0.08941620367747521
Acceptance Statistics
Statistic{name='Acceptance Statistics', n=10000.0, avg=0.785899999999997, sd=0.41021703743479404, ci=[0.7778589276061466, 0.7939410723938475]}
BatchStatistic{name='X_1', n=39.0, avg=0.999193515968228, sd=0.0159560164316252, ci=[0.9940211737797846, 1.0043658581566715], lag-1 corr=0.10751413994760596, Total number observed = 10000.0}
BatchStatistic{name='X_2', n=39.0, avg=27.370099404669936, sd=0.6779873978358747, ci=[27.150321314312187, 27.589877495027686], lag-1 corr=-0.11710134097028374, Total number observed = 10000.0}

As we can see from the sampled vectors, there appears to be more mixing.

0.7114637098246581, 23.334752715575693
1.3918884893683938, 27.582854620937724
1.0234882610125577, 28.761501219684373
1.0234882610125577, 28.761501219684373
1.0234882610125577, 28.761501219684373
1.022818982310043, 28.05859569138944
0.6279823315850492, 30.684331865598743
1.2590803294191133, 25.866338857499585
0.9952174851225053, 21.43482917651085
0.9882686966013114, 24.419256539368444
0.9882686966013114, 24.419256539368444
0.5990339635411173, 20.575702628065457

This section provided an introduction to Markov Chain Monte Carlo methods. The topic of MCMC is vast and the proliferation of research and applications has been enormously active in the past 20 years. This introduction was meant to only illustrate some of the key concepts that you need to understand when applying the technique using the KSL. There are many additional issues that we did not address, including:

  • warm up period determination - This has similar characteristics as to that discussed in Section 5.6.1 but because of the structure of Markov Chains, there are some additional theoretical results that could be explored.

  • statistical analysis - As noted in the implementation discussion, the KSL automatically use batch statistics when reporting the MCMC results. There are other procedures, such as standardized time series and others that may be of interest for MCMC.

  • design of efficient samplers - As the example noted, the design of samplers can be challenging work. We did not discuss the Gibbs sampler and I encourage the interested reader to review the suggested references for more details and other samplers.

G References

Banks, J., J. Carson, B. Nelson, and D. Nicol. 2005. Discrete-Event System Simulation. 4th ed. Prentice Hall.
Biller, B., and B. L. Nelson. 2003. “Modeling and Generating Multivarate Time- Series Input Processes Using a Vector Autogressive Technique.” Assoc. Comput. Mach. Trans. Modeling and Comput. Simul. 13: 211–37.
Brooks, Stephen. 1998. “Markov Chain Monte Carlo Method and Its Application.” Journal of the Royal Statistical Society: Series D (The Statistician) 47 (1): 69–100.
Cario, M. C., and B. L. Nelson. 1996. “Autoregressive to Anything: Time Series Input Processes for Simulation.” Operations Research Letters 19: 51–58.
———. 1998. “Numerical Methods for Fitting and Simulating Autoregressive-to-Anything Processes.” INFORMS Journal of Computing 10: 72–81.
Fishman, George. 2006. A First Course in Monte Carlo. Thomson Brooks/Cole.
Geyer, Charles. 2011. “Handbook of Markov Chain Monte Carlo.” In, edited by Galin Jones Steve Brooks Andrew Gelman and Xiao-Li Meng. Vol. 20116022. CRC Handbooks of Modern Statistical Methods. Chapman & Hall.
Livny, M., B. Melamed, and A. K. Tsiolis. 1993. “The Impact of Autocorrelation on Queueing Systems.” Management Science 39 (3): 322–39.
Nadarajah, Saralees, Emmanuel Afuecheta, and Stephen Chan. 2017. “A Compendium of Copulas.” Statistica 77 (4): 279–328. https://doi.org/10.6092/issn.1973-2201/7202.
Nelsen, Roger B. 2004. “Properties and Applications of Copulas : A Brief Survey.” In. https://api.semanticscholar.org/CorpusID:2508363.
Nelson, Roger B. 1999. An Introduction to Copulas. ISBN o-387-98623-5. New York: Springer-Verlag.
Patuwo, B. E., R. L. Disney, and D. C. Mcnickle. 1993. “The Effect of Correlated Arrivals on Queues.” IIE Transactions 25 (3): 105–10.
Pishro-Nik, H. 2014. Introduction to Probability, Statistics, and Random Processes. Kappa Research LLC.
Robert, Christian P., and Wu Changye. n.d. “Markov Chain Monte Carlo Methods, a Survey with Some Frequent Misunderstandings.” http://arxiv.org/abs/2001.06249.
Ross, Sheldon M. 2023. Simulation (6th Edition). Elsevier.
Rubinstein, R., and D. Kroese. 2017. Simulation and the Monte Carlo Method. John Wiley & Sons Inc.
Sklar, A. 1959. “Fonctions de r ́Epartition a ́ n Dimensions Et Leurs Marges.” Publ. Inst. Statist. Univ. Paris 8: 229–31.
Speagle, Joshua S. 2020. “A Conceptual Introduction to Markov Chain Monte Carlo Methods.” 2020. http://arxiv.org/abs/1909.12313.
Van Ravenzwaaij, Pete Cassey, Don, and Scott D. Brown. 2018. “A Simple Introduction to Markov Chain Monte–Carlo Sampling.” Psychonomic Bulletin & Review 25 (1): 143–54.