5.1 Types of Statistical Variables
A simulation experiment occurs when the modeler sets the input parameters to the model and executes the simulation. This causes events to occur and the simulation model to evolve over time. During the execution of the simulation, the behavior of the system is observed and various statistical quantities computed. When the simulation reaches its termination point, the statistical quantities are summarized in the form of output reports.
A simulation experiment may be for a single replication of the model or may have multiple replications. A replication is the generation of one sample path which represents the evolution of the system from its initial conditions to its ending conditions. If you have multiple replications within an experiment, each replication represents a different sample path, starting from the same initial conditions and being driven by the same input parameter settings. Because the randomness within the simulation can be controlled, the underlying random numbers used within each replication of the simulation can be made to be independent. Thus, as the name implies, each replication is an independently generated “repeat” of the simulation.
Within a single sample path (replication), the statistical behavior of the model can be observed.
Definition 5.1 (Within Replication Statistic) The statistical quantities collected during a replication are called within replication statistics.
Definition 5.2 (Across Replication Statistic) The statistical quantities collected across replications are called across replication statistics. Across replication statistics are collected based on the observation of the final values of within replication statistics.
Within replication statistics are collected based on the observation of the sample path and include observations on entities, state changes, etc. that occur during a sample path execution. The observations used to form within replication statistics are not likely to be independent and identically distributed. Since across replication statistics are formed from the final values of within replication statistics, one observation per replication is available. Since each replication is considered independent, the observations that form the sample for across replication statistics are likely to be independent and identically distributed. The statistical properties of within and across replication statistics are inherently different and require different methods of analysis. Of the two, within replication statistics are the more challenging from a statistical standpoint.
As we saw in section 4.3 of Chapter 4, there are two primary
types of observations: tally and time-persistent. Tally data
represent a sequence of equally weighted data values that do not persist
over time. This type of data is associated with the duration or interval of time that an object is in a particular state or how often the object is in a particular state. As such it is observed by marking
(tallying) the time that the object enters the state and the time that
the object exits the state. Once the state change takes place, the
observation is over (it is gone, it does not persist, etc.). If we did
not observe the state change, then we would have missed the observation.
The time spent in queue, the count of the number of customers served,
whether or not a particular customer waited longer than 10 minutes are
all examples of tally data. We have used the KSL Response class to collect this type of data.
Time-persistent observations represent a sequence of values that persist
over some specified amount of time with that value being weighted by the
amount of time over which the value persists. These observations are
directly associated with the values of the state variables within the
model. The value of a time-persistent observation persists in time. For
example, the number of customers in the system is a common state
variable. If we want to collect the average number of customers in the
system over time, then this will be a time-persistent statistic. While
the value of the number of customers in the system changes at discrete
points in time, it holds (or persists with) that value over a duration
of time. This is why it is called a time-persistent variable. We have used the KSL TWResponse class to collect this type of data.
Figure 5.1 illustrates a single sample path for the number of customers in a queue over a period of time. From this sample path, events and subsequent statistical quantities can be observed.
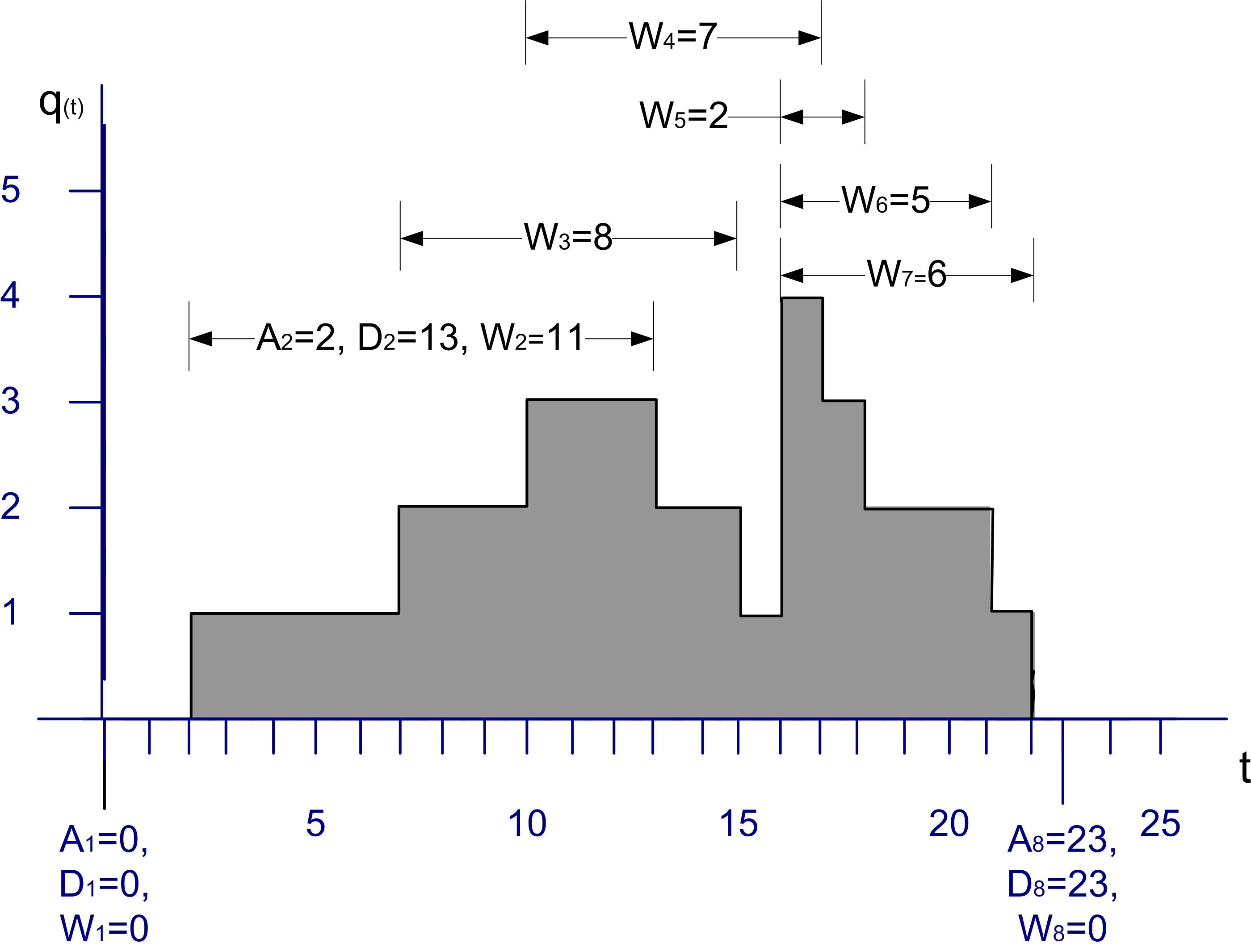
Figure 5.1: Sample Path for Tally and Time-Persistent Data
Let \(A_i \; i = 1 \ldots n\) represent the time that the \(i^{th}\) customer enters the queue
Let \(D_i \; i = 1 \ldots n\) represent the time that the \(i^{th}\) customer exits the queue
Let \(W_i = D_i - A_i \; i = 1 \ldots n\) represent the time that the \(i^{th}\) customer spends in the queue
Thus, \(W_i \; i = 1 \ldots n\) represents the sequence of wait times for the queue, each of which can be individually observed and tallied. This is tally type data because the customer enters a state (the queued state) at time \(A_i\) and exits the state at time \(D_i\). When the customer exits the queue at time \(D_i\), the waiting time in queue, \(W_i = D_i - A_i\) can be observed or tallied. \(W_i\) is only observable at the instant \(D_i\). This makes \(W_i\) tally based data and, once observed, its value never changes again with respect to time. Tally data is most often associated with an entity that is moving through states that are implied by the simulation model. An observation becomes available each time the entity enters and subsequently exits the state.
With tally data it is natural to compute the sample average as a measure of the central tendency of the data. Assume that you can observe \(n\) customers entering and existing the queue, then the average waiting time across the \(n\) customers is given by:
\[\bar{W}(n) = \dfrac{1}{n} \sum_{i=1}^{n} W_{i}\]
Many other statistical quantities, such as the minimum, maximum, and sample variance, etc. can also be computed from these observations. Unfortunately, within replication data is often (if not always) correlated with respect to time. In other words, within replication observations like, \(W_i \, i = 1 \ldots n\), are not statistically independent. In fact, they are likely to also not be identically distributed. Both of these issues will be discussed when the analysis of infinite horizon or steady state simulation models is presented.
The other type of statistical variable encountered within a replication is based on time-persistent observations. Let \(q(t), t_0 < t \leq t_n\) be the number of customers in the queue at time \(t\). Note that \(q(t) \in \lbrace 0,1,2,\ldots\rbrace\). As illustrated in Figure 5.1, \(q(t)\) is a function of time (a step function in this particular case). That is, for a given (realized) sample path, \(q(t)\) is a function that returns the number of customers in the queue at time \(t\).
In simulation, we compute the time-average:
\[\bar{L}_q(n) = \frac{1}{t_n - t_0} \int_{t_0}^{t_n} q(t) \mathrm{d}t\]
This function represents the average with respect to time of the given state variable. This type of statistical variable is called time-persistent because \(q(t)\) is a function of time (i.e. it persists over time).
Tally-based statistics and time-persistent statistics both are collected during a replication and form within replication statistical quantities. When we compute statistics across the replications, we call these statistics across replication statistics.
Now that we understand the type of data that occurs within a replication, we need to develop an understanding for the types of simulation situations that require specialized statistical analysis. The next section introduces this important topic.