5.4 Capturing Output for a Simple Finite Horizon Simulation

In this section, we will build a model for a simple finite horizon simulation with a couple of new modeling issues to handle. However, the primary focus of this section is to illustrate how to capture and report statistical results using the KSL. Let’s start with an outline of the example system to be modeled.

Example 5.1 (Pallet Processing Work Center) A truckload of pallets arrives overnight to a facility. Within the truck there are a random number of pallets. The number of pallets can be modeled with a binomial random variable with mean of 80 and a variance of 16. This translates to parameters \(n=100\) and \(p=0.8\). Each individual pallet is unloaded and transported to a work center for processing, one at a time, sequentially until all pallets are delivered. The unloading and transport time is exponentially distributed with a mean of 5 minutes. Once a pallet arrives at the workcenter it requires 1 of 2 workers to be processed. If a worker is available, the pallet is immediately processed by a worker. If no workers are available, the pallet waits in a FIFO line until a worker becomes available. The time to process the pallet involves breaking down and processing each package on the pallet. The time to process an entire pallet can be modeled with a triangular distribution with a minimum time of 8 minutes, a most likely time of 12 minutes, and a maximum time of 15 minutes. The work at the workcenter continues until all pallets are processed for the day. The facility manager is interested in how long the pallets wait at the workcenter and how long it takes for all pallets to be completed on a given day. In addition, the manager is interested in the probability that there is overtime. That is, the chance that the total time to process the pallets is more than 480 minutes.

This example is a finite horizon simulation because there are a finite (but random) number of pallets to be processed such that the simulation will run until all pallets are processed. The system starts with an arrival of a random number of pallets, that are then processed until all pallets are completed. Therefore there is a well defined starting and ending point for the simulation. Although we do no know when the simulation will end, there is a well-specified condition (all pallets processed) that governs the ending of the simulation. Thus, while the time horizon may be random, it is still finite. Conceptually, this modeling situation is very similar to the pharmacy model discussed in Section 4.4.4. Thus, the implementation of the model will be very similar to the pharmacy model example, but with a couple of minor differences to handle the finite number of pallets that arrive and to capture statistics about the total processing time. The full code is available with the examples. This presentation focuses on new concepts.

As for previous modeling, we define and use random variables to represent the randomness within the model.

class PalletWorkCenter(
    parent: ModelElement,
    numWorkers: Int = 2,
    numPallets: RandomIfc = BinomialRV(0.8, 100, 1),
    transportTime: RandomIfc = ExponentialRV(5.0, 2),
    processingTime: RandomIfc = TriangularRV(8.0, 12.0, 15.0, 3)
) :
    ModelElement(parent, theName = null) {
    
    init {
        require(numWorkers >= 1) { "The number of workers must be >= 1" }
    }
    
    private val myProcessingTimeRV: RandomVariable = RandomVariable(this, processingTime)
    val processingTimeRV: RandomSourceCIfc
        get() = myProcessingTimeRV
    private val myTransportTimeRV: RandomVariable = RandomVariable(parent, transportTime)
    val transportTimeRV: RandomSourceCIfc
        get() = myTransportTimeRV
    private val myNumPalletsRV: RandomVariable = RandomVariable(parent, numPallets)
    val numPalletsRV: RandomSourceCIfc
        get() = myNumPalletsRV

Notice that we defined the random variables as default parameters of the constructor and assign them to relevant properties within the class body. To capture the total time to process the pallets and the probability of overtime, we define two response variables. Notice that the probability of overtime is implemented as an IndicatorResponse that observes the total processing time.

    private val myTotalProcessingTime = Response(this, "Total Processing Time")
    val totalProcessingTime: ResponseCIfc
        get() = myTotalProcessingTime
    private val myOverTime: IndicatorResponse = IndicatorResponse({ x -> x >= 480.0 }, myTotalProcessingTime, "P{total time > 480 minutes}")
    val probOfOverTime: ResponseCIfc
        get() = myOverTime

The main logic of arrivals to the work center and completions of the pallets is essentially the same as previously discussed. The main difference here is that there is a finite number of pallets that need to be created. While there are many ways to represent this situation (e.g. use an EventGenerator), this presentation keeps it simple. The first two lines of this code snippet, capture the functional references for the end of service and end of transport event actions. We have seen this kind of code before. Then, a variable, numToProcess, is defined. This variable will hold the randomly generated number of pallets to process and is assigned in the initialize() method. Within the initialize() method, the transport of the first pallet is scheduled with the provided transport time random variable.

    private val endServiceEvent = this::endOfService
    private val endTransportEvent = this::endTransport
    
    var numToProcess: Int = 0
    
    override fun initialize() {
        numToProcess = myNumPalletsRV.value.toInt()
        schedule(endTransportEvent, myTransportTimeRV)
    }

    private fun endTransport(event: KSLEvent<Nothing>) {
        if (numToProcess >= 1) {
            schedule(endTransportEvent, myTransportTimeRV)
            numToProcess = numToProcess - 1
        }
        val pallet = QObject()
        arrivalAtWorkCenter(pallet)
    }

The endTransport event action checks to see if there are more pallets to transport and if so schedules the end of the next transport. In addition, it creates a QObject that is sent to the work center for processing via the arrivalAtWorkCenter method. As shown in the following code, the arrival and end of service actions are essentially the same as in the previous pharmacy example.

    private fun arrivalAtWorkCenter(pallet: QObject) {
        myNS.increment() // new pallet arrived
        myPalletQ.enqueue(pallet) // enqueue the newly arriving pallet
        if (myNumBusy.value < numWorkers) { // server available
            myNumBusy.increment() // make server busy
            val nextPallet: QObject? = myPalletQ.removeNext() //remove the next pallet
            // schedule end of service, include the pallet as the event's message
            schedule(endServiceEvent, myProcessingTimeRV, nextPallet)
        }
    }

    private fun endOfService(event: KSLEvent<QObject>) {
        myNumBusy.decrement() // pallet is leaving server is freed
        if (!myPalletQ.isEmpty) { // queue is not empty
            val nextPallet: QObject? = myPalletQ.removeNext() //remove the next pallet
            myNumBusy.increment() // make server busy
            // schedule end of service
            schedule(endServiceEvent, myProcessingTimeRV, nextPallet)
        }
        departSystem(event.message!!)
    }

Finally, we have the statistical collection code. The departSystem method captures the time in the system and the number of pallet processed. Howevever, we see something new within a method called replicationEnded()

    private fun departSystem(completedPallet: QObject) {
        mySysTime.value = (time - completedPallet.createTime)
        myNS.decrement() // pallet left system
        myNumProcessed.increment()
    }

    override fun replicationEnded() {
        myTotalProcessingTime.value = time
    }

Recall the overview of how the underlying simulation code is processed from Section 4.4.2.2 of Chapter 4. Step 2(e) of that discussion notes that the actions associated with the end of replication logic is automatically executed. Just like the initialize() method every model element has a replicationEnded() method. This method is called automatically for every model element infinitesimally before the end of the simulation replication. Thus, statistical collection can be implemented without the concern that the statistical accumulators will be cleared after the replication. Thus, observations within the replicationEnded() method are still within the replication (i.e. they produce within replication data). In the above code snippet, the Response myTotalProcessingTime is assigned the current simulation time, which happens to be the time at which the processing of the pallets was completed. This occurs because after the appropriate number of transports are scheduled, no further pallets arrive to be processed at the work center. Thus, eventually, there will be no more events to process, and according to Step 2(d) of Section 4.4.2.2, this will cause the execution of the current replication to stop and proceed with any end of replication model logic. Thus, this logic captures the total time to process the pallets. In addition, because an IndicatorResponse was also attached to myTotalProcessingTime the collection of the probability of over time will also be captured. The basic results of the model are as follows:

Statistical Summary Report

Name Count Average Half-Width
NumBusyWorkers 10.0 1.9174709267367938 0.04615844720276659
PalletQ:NumInQ 10.0 7.397061723049351 2.18200524048673
PalletQ:TimeInQ 10.0 44.65967086387171 12.756611150942986
Num Pallets at WC 10.0 9.314532649786145 2.2091925024424928
System Time 10.0 56.32044792861602 12.742871337228127
Total Processing Time 10.0 489.20830013021094 16.326885695752644
P{total time > 480 minutes} 10.0 0.6 0.369408717216522
Num Processed 10.0 80.4 2.5054518188054615

If you are paying attention to the presentation of previous summary statistics, you will notice that the last summary report is presented in a nice tabular format. This output was actually generated by the KSL class SimulationReporter, which can make MarkDown output. This and additional output capturing will be discussed in the next section.

5.4.1 KSL Functionality for Capturing Statistical Results

This section presents a number of methods that can be used to capture and report the results from a KSL model. The following topics will be covered:

  • Automatically capturing within and across replication results to comma separated value files
  • Capturing replication data via the ReplicationDataCollector class
  • Tracing a response variable via the ResponseTrace class
  • Using the SimulationReporter class to output results in MarkDown and adjusting the confidence level of the reports
  • Capturing all simulation results to a database using the KSLDatabaseObserver class and illustrating how to get results from the database

These topics will be discussed within the context of the pallet example of the previous section. The main method for running the pallet example was expanded to illustrate additional data collection functionality. It is unlikely that you will want to capture results both as comma separated value files and using a database, but both approaches are illustrated. If you are familiar with database technologies, then using the database will likely serve most if not all of your needs.

fun main() {
    val model = Model("Pallet Processing", autoCSVReports = true)
    model.numberOfReplications = 10
    model.experimentName = "Two Workers"
    // add the model element to the main model
    val palletWorkCenter = PalletWorkCenter(model)

    // demonstrate how to capture a trace of a response variable
    val trace = ResponseTrace(palletWorkCenter.numInSystem)

    // demonstrate capture of replication data for specific response variables
    val repData = ReplicationDataCollector(model)
    repData.addResponse(palletWorkCenter.totalProcessingTime)
    repData.addResponse(palletWorkCenter.probOfOverTime)

    // demonstrate capturing data to database with an observer
    val kslDatabaseObserver = KSLDatabaseObserver(model)

    // simulate the model
    model.simulate()

    // demonstrate that reports can have specified confidence level
    val sr = model.simulationReporter
    sr.printHalfWidthSummaryReport(confLevel = .99)

    // show that report can be written to MarkDown as a table in the output directory
    var out = model.outputDirectory.createPrintWriter("hwSummary.md")
    sr.writeHalfWidthSummaryReportAsMarkDown(out)
    println()

    //output the collected replication data to prove it was captured
    println(repData)

    // use the database to create a Kotlin DataFrame
    val dataFrame = kslDatabaseObserver.db.acrossReplicationViewStatistics
    println(dataFrame)

    model.experimentName = "Three Workers"
    palletWorkCenter.numWorkers = 3
    model.simulate()

    out = model.outputDirectory.createPrintWriter("AcrossExperimentResults.md")
    kslDatabaseObserver.db.writeTableAsMarkdown("ACROSS_REP_VIEW", out)
}

Let’s start with automatically collecting responses within comma separated value (CSV) files and how to find them in the file system.

The first thing to note is how the output from a KSL simulation is organized. The KSL model class allows the user to specify the output directory for the model results. If the user does not specify an output directory, the default directory will be within a folder called kslOutput that will be created within the same folder that the model was executed. That is, the current working directory for the user. Within the kslOutput directory all KSL related work will be stored. In particular, a unique directory derived from the name of the simulation will be created to hold all the results from a particular simulation model’s execution. These locations can be changed, but the defaults are well-specified and useful.

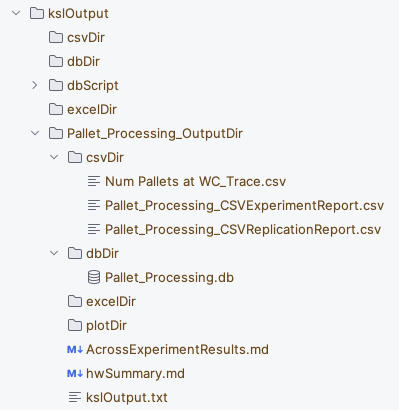
Organization of KSL Output Directories

Figure 5.2: Organization of KSL Output Directories

Figure 5.2 illustrates the output directory after running the pallet model. You should see the kslOutput directory and a directory called Pallet_Processing_OutputDir. Within the Pallet_Processing_OutputDir directory there are folders called db and excel. These folders are the default directories for holding database related files and Excel related output files. Within the db folder there is a file called MainModel.db, which is an SQLite database that was created to hold the KSL simulation results. Then, there are two files called hwSummary.md and kslOutput.txt. There are also three CSV files, two labeled with _ExperimentReport.csv and _ReplicationReport.csv, and one labeled with _Trace.csv. This labeling scheme is the default and is derived from the context of the item. The setting of the autoCSVReports option to true when creating the model is what caused the two files labeled with _ExperimentReport.csv and with _ReplicationReport.csv to be produced. The following table is from Pallet_Processing_CSVReplicationReport.csv.

Table 4.3: Table 5.1: First 8 columns and 5 Rows of Pallet_Processing_CSVReplicationReport.csv.
SimName ModelName ExpName RepNum ResponseType ResponseID ResponseName Statistic.Name
Pallet Processing MainModel Two Workers 1 TWResponse 7 NumBusyWorkers NumBusyWorkers
Pallet Processing MainModel Two Workers 1 TWResponse 9 PalletQ:NumInQ PalletQ:NumInQ
Pallet Processing MainModel Two Workers 1 Response 10 PalletQ:TimeInQ PalletQ:TimeInQ
Pallet Processing MainModel Two Workers 1 TWResponse 11 Num Pallets at WC Num Pallets at WC
Pallet Processing MainModel Two Workers 1 Response 12 System Time System Time
Pallet Processing MainModel Two Workers 1 Response 14 Total Processing Time Total Processing Time

As can be seen in the previous table, the replication report has information about the simulation, model, experiment, replication number, response type, and name. In total, the replication report has 19 columns and will contain every replication observation for every response variable in the model. Notice that the experiment name is the string (“Two Workers”) that was provided for the experiment’s name on line 4 of the main method.

The following table illustrates columns 8 through 12 of the file.

Table 4.5: Table 5.1: Next 5 columns and 5 Rows of Pallet_Processing_CSVReplicationReport.csv.
Statistic.Name Count Average Minimum Maximum
NumBusyWorkers 79 1.889149 0.00000 2.00000
PalletQ:NumInQ 150 3.288616 0.00000 7.00000
PalletQ:TimeInQ 76 20.874804 0.00000 41.56455
Num Pallets at WC 152 5.177765 0.00000 9.00000
System Time 76 32.866354 12.61226 52.43014
Total Processing Time 1 482.417201 482.41720 482.41720

This data can be easily processed by other of statistical programs such as R or opened directly within Excel. The following table is from Pallet_Processing_CSVExperimentReport.csv and represents the across replication summary statistics for the responses and counters in the model.

Table 4.7: Table 5.2: Columns 7-15 and 9 Rows of Pallet_Processing_CSVExperimentReport.csv.
Statistic.Name Count Average Standard.Deviation Standard.Error Half.width Confidence.Level Minimum Maximum
NumBusyWorkers 10 1.917471 0.0645251 0.0204046 0.0461584 0.95 1.772891 1.990707
PalletQ:NumInQ 10 7.397062 3.0502330 0.9645684 2.1820052 0.95 3.288616 11.554069
PalletQ:TimeInQ 10 44.659671 17.8325128 5.6391357 12.7566112 0.95 20.874804 68.107389
Num Pallets at WC 10 9.314533 3.0882382 0.9765867 2.2091925 0.95 5.177765 13.529605
System Time 10 56.320448 17.8133058 5.6330619 12.7428713 0.95 32.866354 79.752513
Total Processing Time 10 489.208300 22.8234125 7.2173967 16.3268857 0.95 461.544205 534.281150
P{total time > 480 minutes} 10 0.600000 0.5163978 0.1632993 0.3694087 0.95 0.000000 1.000000
Num Processed 10 80.400000 3.5023801 1.1075498 2.5054518 0.95 75.000000 87.000000
NumBusyWorkers 10 2.239980 0.1880656 0.0594716 0.1345340 0.95 1.864706 2.553376

As can be noted in the table, this is essentially the same information as reported in the output summary statistics. Again, these responses are automatically captured by simply setting the autoCSVReports option to true when creating the model.

A user may want to trace the values of specific response variables to files for post processing or display. This can be accomplished by using the ResponseTrace class. This code snippet, attaches an instance of the ResponseTrace class to the number in system response variable (palletWorkCenter.numInSystem) via the property that exposes the response to clients of the class. The user needs either an instance of the response variable or the exact name of the variable. This is one reason why the public property numInSystem was supplied.

    // demonstrate how to capture a trace of a response variable
    val trace = ResponseTrace(palletWorkCenter.numInSystem)

Attaching an instance of the ResponseTrace class to a response causes the trace to observe any value changes of the variable.

Table 4.9: Table 5.3: First 10 rows of Num Pallets at WC_Trace.csv.
n t x(t) t(n-1) x(t(n-1)) w r nr sim model exp
1 0.000000 0 0.000000 0 0.0000000 1 1 Pallet Processing MainModel Two Workers
2 7.126878 1 0.000000 0 7.1268782 1 2 Pallet Processing MainModel Two Workers
3 19.739140 0 7.126878 1 12.6122616 1 3 Pallet Processing MainModel Two Workers
4 26.281530 1 19.739140 0 6.5423903 1 4 Pallet Processing MainModel Two Workers
5 32.059599 2 26.281530 1 5.7780694 1 5 Pallet Processing MainModel Two Workers
6 33.697050 3 32.059599 2 1.6374507 1 6 Pallet Processing MainModel Two Workers
7 34.220684 4 33.697050 3 0.5236344 1 7 Pallet Processing MainModel Two Workers
8 38.888641 5 34.220684 4 4.6679570 1 8 Pallet Processing MainModel Two Workers
9 40.431432 4 38.888641 5 1.5427903 1 9 Pallet Processing MainModel Two Workers
10 46.112274 5 40.431432 4 5.6808427 1 10 Pallet Processing MainModel Two Workers
11 46.776521 4 46.112274 5 0.6642467 1 11 Pallet Processing MainModel Two Workers

In the output, \(x(t)\) is the value of the variable at time \(t\). Also, \(t_{n-1}\) is the previous time and \(x(t_{n-1})\) is the value of the variable at the previous time. This facilitates plotting of the variable values over time. The column \(r\) represents the replication number and the column \(nr\) represents the number of observations in the current replication. These files can become quite large. Thus, it is recommended that you take the trace off when not needed and limit your trace coverage.

Before discussing the KSL database, note that the previously mentioned MarkDown functionality is implemented with the following code:

    // show that report can be written to MarkDown as a table in the output directory
    val out = model.outputDirectory.createPrintWriter("hwSummary.md")
    sr.writeHalfWidthSummaryReportAsMarkDown(out)

This code uses the model’s output directory property to create a file based on a PrintWriter in the directory and then uses the PrintWriter instance via the SimulationReporter class. The KSL has a utility class found in the ksl.io package called MarkDown that facilitates simple construction of MarkDown text constructs, especially tables and rows within tables.

The Functionality of the SimulationReporter Class

Figure 5.3: The Functionality of the SimulationReporter Class

As shown in Figure 5.3, the SimualationReporter class has functionality to write simulation results in a number of formats. If you are a LaTeX user, you may want to try the functionality to create LaTeX tables. Besides reporting functionality, there is some limited ability to create copies of the underlying statistical objects. But, to directly get raw data, you should use the ReplicationDataCollector class or the KSL database.

The ReplicationDataCollector class and the ExperimentDataCollector class (not discussed here) are observers that can be attached to the model that will hold replication data and across experiment data, respectively. The collection can be limited to specific responses or all responses. The classes will hold the data observed from the simulation in memory (via arrays). These arrays can be accessed to perform post processing within code as needed.

    // demonstrate capture of replication data for specific response variables
    val repData = ReplicationDataCollector(model)
    repData.addResponse(palletWorkCenter.totalProcessingTime)
    repData.addResponse(palletWorkCenter.probOfOverTime)

This code creates a ReplicationDataCollector instance and configures the instance to collect the replication data for the total processing time and probability of over time responses. A simple output of the first 10 values of the data arrays is shown here.

   Total Processing Time P{total time > 480 minutes}
 0            482.417201                         1.0
 1            461.544205                         0.0
 2            521.417293                         1.0
 3            476.025297                         0.0
 4            534.281150                         1.0
 5            485.735690                         1.0
 6            477.468018                         0.0
 7            482.557886                         1.0
 8            499.628817                         1.0
 9            471.007443                         0.0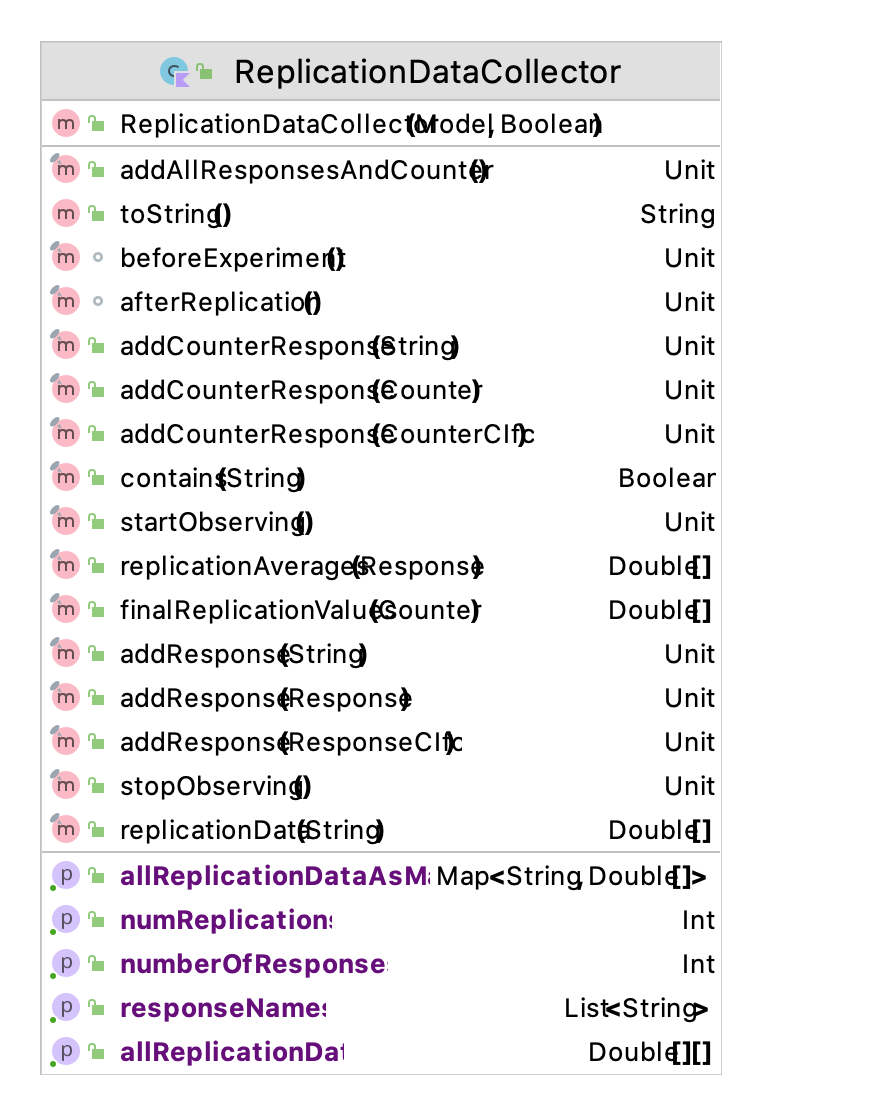
The Functionality of the ReplicationDataCollector Class

Figure 5.4: The Functionality of the ReplicationDataCollector Class

The most notable functionality shown in Figure 5.4 is the allReplicationDataAsMap property. The map is indexed by the name of the response as the key and the replication data as a DoubleArray. Thus, any response data that you need can be readily access within memory. The ExperimentDataCollector class (not discussed here) has similar functionality but will capture the data across different experiments. Experiment functionality will be discussed in a later chapter.

Now, let’s discuss the most useful KSL functionality for capturing simulation data, the KSLDatabase class. The following code creates an observer of the model in the form of a KSLDatabaseObserver. This class can be attached to a model and then will collect and insert all response and counter related statistical quantities into a well-structured database. The default database is an SQLite database but other database engines will also work. There is built in functionality for creating Derby and PostgreSQL based databases.

The Functionality of the KSLDatabase Class

Figure 5.5: The Functionality of the KSLDatabase Class

Figure 5.5 presents the functionality of the KSLDatabase class. This class is built on top of functionality within the KSL ksl.utilities.io.dbutil package for creating databases via the DatabaseIfc interface and the Database class. Here our focus is on how the data from a KSL simulation is captured and stored. The capturing occurs because the user attaches an instance of a KSLDatabaseObserver to a model as shown in this code snippet.

    // demonstrate capturing data to database with an observer
    val kslDatabaseObserver = KSLDatabaseObserver(model)

This code creates an observer that accesses the simulation data after each replication and stores it within a database. The database will be stored within the dbDir folder of the simulation model’s output directory. Note that if you execute any simulation that has the same name as a previously executed simulation then the previous database will be deleted and recreated. This might cause you to lose previous simulation results. This behavior is the default because generally, when you re-run your simulation you want the results of that run to be written into the database. However, it is possible to not overwrite the database and store additional experiments within the same database. To do this, get an instance of an existing KSL database before creating the KSLDatabaseObserver. In addition, by changing the name of the experiment associated with the model, then the results from different experiments can be stored in the same database. This approach is useful when comparing results across simulation configurations.

The database will have the table structure shown in Figure 5.6.

KSL Database Tables

Figure 5.6: KSL Database Tables

The KSL database consists of six tables that capture information and data concerning the execution of a simulation and resulting statistical quantities. Figure 5.6 presents the database diagram for the KSL_DB database schema.

  • SIMULATION_RUN – contains information about the simulation runs that are contained within the database. Such information as the name of the simulation, model, and experiment are captured. In addition, time stamps of the start and end of the experiment, the number of replications, the replication length, the length of the warm up period and options concerning stream control.
  • MODEL_ELEMENT contains information about the instances of ModelElement that were used within the execution of the simulation run. A model element has an identifier that is considered unique to the simulation run. That is, the simulation run ID and the model element ID are the primary key of this table. The name of the model element, its class type, the name and ID of its parent element are also held for each entity in MODEL_ELEMENT. The parent/child relationship permits an understanding of the model element hierarchy that was present when the simulation executed.
  • WITHIN_REP_STAT contains information about within replication statistical quantities associated with TWResponse and Response instances from each replication of a set of replications of the simulation. The name, count, average, minimum, maximum, weighted sum, sum of weights, weighted sum of squares, last observed value, and last observed weight are all captured.
  • WITHIN_REP_COUNTER_STAT contains information about with replication observations associated with Counters used within the model. The name of the counter and the its value at the end of the replication are captured for each replication of a set of replications of the simulation.
  • ACROSS_REP_STAT contains information about the across replication statistics associated with TWResponse, Response, and Counter instances within the model. Statistical summary information across the replications is automatically stored.
  • BATCH_STAT contains information about the batch statistics associated with TWResponse, Response, and Counter instances within the model. Statistical summary information across the batches is automatically stored.
  • HISTOGRAM contains the results from HistogramResponse instances when they are used within a model.
  • FREQUENCY contains the results from IntegerFrequencyResponse instances when they are used within a model.
  • EXPERIMENT holds information across experimental runs. This is illustrate in Section 5.8 and Section D.9 of Appendix D.
  • CONTROL holds the controls associated with a model as discussed in Section 5.8.1.
  • RV_PARAMETER holds the random variables and their parameters as discussed in Section 5.8.2.

In addition to the base tables, the KSL database contains views of its underlying tables to facilitate simpler data extraction. Figure 5.7 presents the pre-defined views for the KSL database. The views, in essence, reduce the amount of information to the most likely used sets of data for the across replication, batch, and within replication captured statistical quantities. In addition, the PW_DIFF_WITHIN_REP_VIEW holds all pairwise differences for every response variable, time weighted variable, or counter from across all experiments within the database. This view reports (\(A - B\)) for every within replication ending average, where \(A\) is a simulation run that has higher simulation ID than \(B\) and they represent an individual performance measure. From this view, pairwise statistics can be computed across all replications. Since simulation IDs are assigned sequentially within the database, the lower the ID the earlier the simulation was executed.

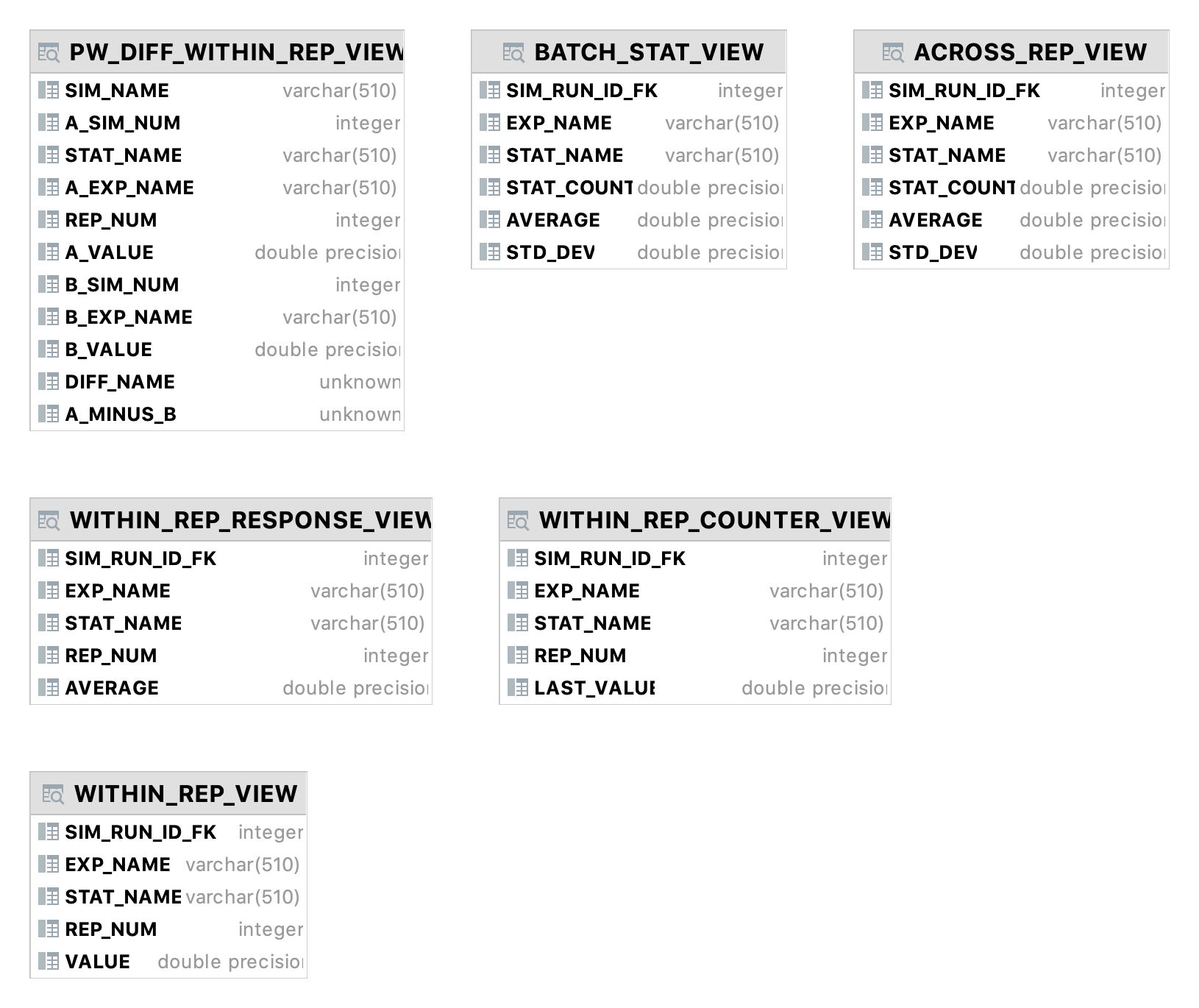
KSL Database Views

Figure 5.7: KSL Database Views

The information within the SIMULATION_RUN, MODEL_ELEMENT, WITHIN_REP_STAT, and WITHIN_REP_COUNTER_STAT tables are written to the database at the end of each replication. The ACROSS_REP_STAT and BATCH_STAT tables are filled after the entire experiment is completed. Even though the ACROSS_REP_STAT table could be constructed directly from the data captured within the tables holding with replication data, this is not done. Instead, the across replication statistics are directly written from the simulation after all replications of an experiment are completed.

As an illustration consider running a simulation multiple times within the same program execution but with different parameters. The following code illustrates how this might be achieved. Please note the following code at the bottom of the main execution routine.

    model.experimentName = "Three Workers"
    palletWorkCenter.numWorkers = 3
    model.simulate()

    out = model.outputDirectory.createPrintWriter("AcrossExperimentResults.md")
    kslDatabaseObserver.db.writeTableAsMarkdown("ACROSS_REP_VIEW", out)

In this code, the experiment name has been updated to “Three Workers” and the number of workers property changed. The model was simulated again. The underlying KSL database was accessed to write out the across replication view statistics. As shown in the following table, the database retained the data from the first execution and added the data from the second execution. This only occurred because the name of the experiment was changed between calls to the simulate() method. In the results, we see that adding a worker causes the chance of overtime to become zero.

Table: ACROSS_REP_VIEW

SIM_ID EXP_NAME STAT_NAME COUNT AVERAGE STD_DEV
1 Two Workers Num Pallets at WC 10.0 9.3145 3.0882
2 Three Workers Num Pallets at WC 10.0 3.2083 0.7035
1 Two Workers Num Processed 10.0 80.4 3.5023
2 Three Workers Num Processed 10.0 79.1 4.1217
1 Two Workers NumBusyWorkers 10.0 1.9174 0.0645
2 Three Workers NumBusyWorkers 10.0 2.2399 0.1881
1 Two Workers PalletQ:NumInQ 10.0 7.3971 3.0502
2 Three Workers PalletQ:NumInQ 10.0 0.9683 0.5725
1 Two Workers PalletQ:TimeInQ 10.0 44.6596 17.8325
2 Three Workers PalletQ:TimeInQ 10.0 4.9261 2.6231
1 Two Workers P{total time > 480 minutes} 10.0 0.6 0.5163
2 Three Workers P{total time > 480 minutes} 10.0 0.0 0.0
1 Two Workers System Time 10.0 56.32044792861602 17.8133
2 Three Workers System Time 10.0 16.5628 2.6346
1 Two Workers Total Processing Time 10.0 489.2083 22.8234
2 Three Workers Total Processing Time 10.0 412.6305 28.1443

A KSLDatabase instance is constructed to hold the data from any KSL simulation. As such, a simulation execution can have many observers and thus could have any number of KSLDatabase instances that collect data from the execution. The most common case for multiple databases would be the use of an embedded database as well as a database that is stored on a remote database server.

Once you have a database that contains the schema to hold KSL based data, you can continue to write results to that database as much as you want. If your database is on a server, then you can easily collect data from different simulation executions that occur on different computers by referencing the database on the server. Therefore, if you are running multiple simulation runs in parallel on different computers or in the “cloud”, you should be able to capture the data from the simulation runs into one database.

5.4.2 Additional Remarks

The functionality of the KSL database depends upon how Response, TWResponse, and Counter instances are named within a KSL model. A KSL model is organized into a tree of ModelElement instances with the instance of the Model at the top of the tree. The Model instance for the simulation model contains instances of ModelElement, which are referred to as children of the parent model element. Each model element instance can have zero or more children, and those children can have children, etc. Each ModelElement instance must have a unique integer ID and a unique name. The unique integer ID is automatically provided when a ModelElement instance is created. The user can supply a name for a ModelElement instance when creating the instance. The name must be unique within the simulation model.

A recommended practice to ensure that model element names are unique is to use the name of the parent model element as part of the name. If the parent name is unique, then all children names will be unique relative to any other model elements. For example, in the following code name references the name of the current model element (an instance of Queue), which is serving as the parent for the children model element (responses) declared within the constructor body. Unfortunately, this approach may lead to very long names if the model element hierarchy is deep.

    protected val myNumInQ: TWResponse = TWResponse(this, name = "${name}:NumInQ")
    override val numInQ : TWResponseCIfc
        get() = myNumInQ

    protected val myTimeInQ: Response = Response(this, name = "${name}:TimeInQ")
    override val timeInQ : ResponseCIfc
        get() = myTimeInQ

The name supplied to the TWResponse and Response constructors will cause the underlying statistic to have the indicated names. The response’s name cannot be changed once it is set. The statistic name is important for referencing statistical data within the KSL database.

One complicating factor involves using the KSL database to analyze the results from multiple simulation models. In order to more readily compare the results of the same performance measure between two different simulation models, the user should try to ensure that the names of the performance measures are the same. If the above recommended naming practice is used, the names of the statistics may depend on the order in which the model element instances are created and added to the model element hierarchy. If the model structure never changes between different simulation models then this will not present an issue; however, if the structure of the model changes between two different simulation models (which can be the case), the statistic names may be affected. If this issue causes problems, you can always name the desired output responses or counters exactly what you want it to be and use the same name in other simulation models, as long as you ensure unique names.

Since the model element ID is assigned automatically based on the number of model elements created within the model, the model element numbers between two instances of the same simulation model will most likely be different. Thus, there is no guarantee that the IDs will be the same and using the model element ID as part of queries on the KSL database will have to take this into account. You can assume that the name of the underlying statistic is the same as its associated model element and since it is user definable, it is better suited for queries based on the KSL database.

5.4.3 Querying the KSL Database

The KSL database is a database and thus it can be queried from within Kotlin or from other programs. If you have an instance of the KSLDatabase, you can extract information about the simulation run using the methods of the KSLDatabase class. Since the underlying data is stored in a relational database, SQL queries can be used on the database. The discussion of writing and executing SQL queries is beyond the scope of this text. To facilitate output when using the KSL, the KSL has a few methods to be aware of, including:

  • exportAllTablesAsCSV() – writes all the tables to separate CSV files
  • exportDbToExcelWorkbook() – writes all the tables and views to a single Excel workbook
  • multipleComparisonAnalyzerFor(set of experiment name, response name) – returns an instance of the MultipleComparisonAnalyzer class in order to perform a multiple comparison analysis of a set of experiments on a specific response name.
  • a number of properties that return Kotlin data frames of the underlying database tables.

The data frame functionality was illustrated in the following code from the main execution method:

    // use the database to create a Kotlin DataFrame
    val dataFrame = kslDatabaseObserver.db.acrossReplicationViewStatistics
    println(dataFrame)

NOTE! The Kotlin data frames library has excellent capabilities for processing data within a tablular format. The KSL has additional functionality for processing files via its utilities as described in Section D.4 of Appendix D. Also, you might want to explore the extensions for data frames described in Section D.5 of Appendix D.

Once you have the data frame you can employ whatever data wrangling and extraction methods that you need. Finally, because the KSL database is a database, it can be accessed via R or other software programs such as IntelliJ’s DataGrip or DBeaver and additional analysis performed on the KSL simulation data.

Based on the discussion in this section, the KSL has very useful functionality for working with the data generated from your simulation models.