7.3 Examples of Advanced Event Models

This section will illustrate situations where combining event based modeling and process modeling is useful. In addition, we will exam how to simulate an inventory system using the event view.

7.3.1 Modeling Balking and Reneging

This situation has multiple types of customers with different priorities, different service times, and in the case of one type of customer, the desire (or ability) to renege from the system. You can find the completed model file for this section in the chapter files under the name, WalkInHealthClinic.

Example 7.8 (Walk-in Health Care Clinic) A walk-in care clinic has analyzed their operations and they have found that they can classify their walk-in patients into three categories: high priority (urgent need of medical attention), medium priority (need standard medical attention), and low priority (non-urgent need of medical attention). On a typical day during the period of interest there are about 15 arrivals per hour with (25% being high priority, 60% being medium priority, and the remaining being low priority). The clinic is interested in understanding the waiting time for patients at the clinic. Upon arrival to the clinic the patients are triaged by a nurse into one of the three types of patients. This takes only 2-3 minutes uniformly distributed. Then, the patients wait in the waiting room based on their priority. Patients with higher priority are placed at the front of the line. Patients with the same priority are ordered based on a first-come first served basis. The service time distributions of the customers are given as follows.

Priority Service Time Distribution (in minutes)
High Lognormal(\(\mu = 38\), \(\sigma = 8\))
Medium Triangular(16, 22, 28)
Low Lognormal(\(\mu = 12\), \(\sigma = 2\))

The clinic has 4 doctors on staff to attend to the patients during the period of interest. They have found through a survey that if there are more than 10 people waiting for service an arriving low priority patient will exit before being triaged. Finally, they have found that the non-urgent (low priority) patients may depart if they have to wait longer than \(15 \pm 5\) minutes after triage. That is, a non-urgent patient may enter the clinic and begin waiting for a doctor, but if they have to wait more than \(15 \pm 5\) minutes (uniformly distributed) they will decide to renege and leave the clinic without getting service. The clinic would like to estimate the following:

  1. the average system time of each type of patient

  2. the probability that low priority patients balk

  3. the probability that low priority patients renege

Solution to Example 7.8

For this problem, the system is the walk-in clinic, which includes doctors and a triage nurse who serve three types of patients. The system must know how the patients arrive (time between arrival distribution), how to determine the type of the patient, the triage time, the service time by type of patient, and the amount of time that a low priority patient is willing to wait. The following code defines the random variables needed for the modeling as well as the resources. Notice that this code explicitly defines the queue to hold the requests for the doctor. This is done to permit direct access to the reference for the queue during the implementation of reneging.

class WalkInHealthClinic(parent: ModelElement, name: String? = null) : ProcessModel(parent, name) {

    private val myTBArrivals: RVariableIfc = ExponentialRV(6.0, 1)

    private val triageRV = RandomVariable(this, UniformRV(2.0, 3.0, 2))
    private val highRV = RandomVariable(this, LognormalRV(38.0, 8.0 * 8.0, 3))
    private val mediumRV = RandomVariable(this, TriangularRV(16.0, 22.0, 28.0, 4))
    private val lowRV = RandomVariable(this, LognormalRV(12.0, 2.0 * 2.0, 5))

    private val renegeTimeRV = RandomVariable(this, UniformRV(10.0, 20.0, 6))

    private val doctorQ: RequestQ = RequestQ(this, "DoctorQ", discipline = Queue.Discipline.RANKED)
    private val doctorR: ResourceWithQ = ResourceWithQ(this, capacity = 5, queue = doctorQ, name = "Doctors")

    private val triageNurseR: ResourceWithQ = ResourceWithQ(this, capacity = 1, name = "TriageNurse")

    var balkCriteria = 10
        set(value) {
            require(value > 0) { "The balk criteria must be > 0" }
            field = value
        }

In the following code fragment, we use a DEmpiricalList to hold the service distribution for the types of patients. In addition, a map is defined to model the relationship between the type of patient and the priority.

    // set up the service distribution and the random selection
    private val distributions = listOf(highRV, mediumRV, lowRV)
    private val distributionCDF = doubleArrayOf(0.25, 0.85, 1.0)
    private val serviceRV = REmpiricalList(this, distributions, distributionCDF)
    private val typeMap = mapOf(highRV to 1, mediumRV to 2, lowRV to 3)

We will use these constructs within the patient processes. In the following code, we use the serviceRV to randomly assign the service time distribution for the patient and then use the map to assign the patient’s priority based on the service setting. The clinicProcess starts with a test to see if the low priority patient that arrives will balk if the doctor’s waiting queue has too many people. If so, we collect statistics on the balking and exit the process.

    private inner class Patient : Entity() {
        private val service = serviceRV.element

        init {
            priority = typeMap[service]!!
        }

        val clinicProcess = process {
            if ((priority == 3) && (doctorQ.size >= balkCriteria)) {
                // record balking
                balkingProb.value = 1.0
                numBalked.increment()
                return@process
            }
            if (priority == 3){
                balkingProb.value = 0.0
            }
            use(triageNurseR, delayDuration = triageRV)
            // only low priority renege
            if (priority == 3) {
                schedule(this@Patient::renegeAction, renegeTimeRV, message = this@Patient)
            }
            val a = seize(doctorR)
            delay(service)
            release(a)
            if (priority == 3){
                renegingProb.value = 0.0
            }
            val st = time - this@Patient.createTime
            timeInSystem.value = st
            sysTimeMap[priority]?.value = st
            numServed.increment()
        }

Patients that get past the balking logic complete the rest of the process and thus do not balk. A response variable is used to collect this statistic. Then, the patient uses the triage nurse. After using the triage nurse, the low priority patient might need to renege. Thus, the low priority patient schedules the reneging action. All patients proceed to used the doctor. After using the doctor, if the patient is a low priority patient, then the patient must not have reneging and statistics are collected. Finally, statistics are collected upon departure from the process. Let’s take a closer look at the reneging action logic.

        private fun renegeAction(event: KSLEvent<Patient>) {
            val request: ProcessModel.Entity.Request? = doctorQ.find { it.entity == event.message }
            if (request != null) {
                doctorQ.removeAndTerminate(request)
                // reneging statistics
                renegingProb.value = 1.0
                numReneged.increment()
            }
        }

The low priority patient schedules its possible reneging. One can think of this as the patient, setting an alarm clock (the event scheduled by the entity) for when to renege. This must be done because once the low priority patient seizes the doctor it may be suspended and cannot proceed (by itself) to exit the queue after a period of time. Thus, an event is scheduled at the time of the reneging (essentially when the patient’s patience runs out). The above code is the event action. Here, the doctor queue (doctorQ) is searched to find the same entity that scheduled the event. If that entity’s request is found then the request is removed from the doctor queue and reneging statistics are collected. If a request is not found, there is nothing to do because the patient has already started seeing the doctor.

Notice that the removal of the entity from the queue uses the removeAndTerminate() method of the RequestQ class. Since the entity is suspended within the process and is being held in the queue, we must remove the entity’s request from the queue and terminate its process. For more complex termination situations, the user can supply a function to be invoked after the process is terminated via a parameter of the removeAndTerminate() method. For example, such a function could allow for the sending of the removed entity to further processing.

The results from simulating the clinic for 30 days of operation are as follows.

Walk-in Clinic Statistical Summary Report

Name Count Average Half-Width
DoctorQ:NumInQ 30 0.93 0.232
DoctorQ:TimeInQ 30 4.79 1.078
Doctors:InstantaneousUtil 30 0.779 0.026
Doctors:NumBusyUnits 30 3.897 0.129
Doctors:ScheduledUtil 30 0.779 0.026
Doctors:WIP 30 4.828 0.339
TriageNurse:InstantaneousUtil 30 0.421 0.016
TriageNurse:NumBusyUnits 30 0.421 0.016
TriageNurse:ScheduledUtil 30 0.421 0.016
TriageNurse:WIP 30 0.575 0.037
TriageNurse:Q:NumInQ 30 0.154 0.022
TriageNurse:Q:TimeInQ 30 0.889 0.107
Walk-In Clinic:TimeInSystem 30 33.165 1.445
Walk-In Clinic:TimeInSystemHigh 30 43.77 0.851
Walk-In Clinic:TimeInSystemMedium 30 31.47 1.626
Walk-In Clinic:TimeInSystemLow 30 17.188 0.653
Walk-In Clinic:ProbBalking 30 0 0
Walk-In Clinic:ProbReneging 30 0.293 0.075
Doctors:SeizeCount 30 94.733 2.442
TriageNurse:SeizeCount 30 101.233 3.791
Walk-In Clinic:NumServed 30 90.633 2.273
Walk-In Clinic:NumBalked 30 0 0
Walk-In Clinic:NumReneged 30 4.367 1.325

Notice that a fairly high (28%) of the low priority patients renege before seeing the doctor. This may or may not be acceptable in light of the other performance measures for the system. The reader is asked to further explore this model in the exercises. While some analytical work has been done for queuing systems involving balking and reneging, simulation allows for the modeling of more realistic types of queueing situations as well as even more complicated systems. The next subsection will explore such a situation.

7.3.2 Modeling a Reorder Point, Reorder Quantity Inventory Policy

In an inventory system, there are units of an item (e.g. computer printers, etc.) for which customers make demands. If the item is available (in stock) then the customer can receive the item and depart. If the item is not on hand when a demand from a customer arrives then the customer may depart without the item (i.e. lost sales) or the customer may be placed on a list for when the item becomes available (i.e. back ordered). In a sense, the item is like a resource that is consumed by the customer. Unlike the previous notions of a resource, inventory can be replenished. The proper control of the replenishment process is the key to providing adequate customer service. There are two basic questions that must be addressed when controlling the inventory replenishment process: 1) When to order? and 2) How much to order?. If the system does not order enough or does not order at the right time, the system not be able to fill customer demand in a timely manner. Figure 7.9 illustrates a simple inventory system.

A simple reorder point, reorder quantity inventory system

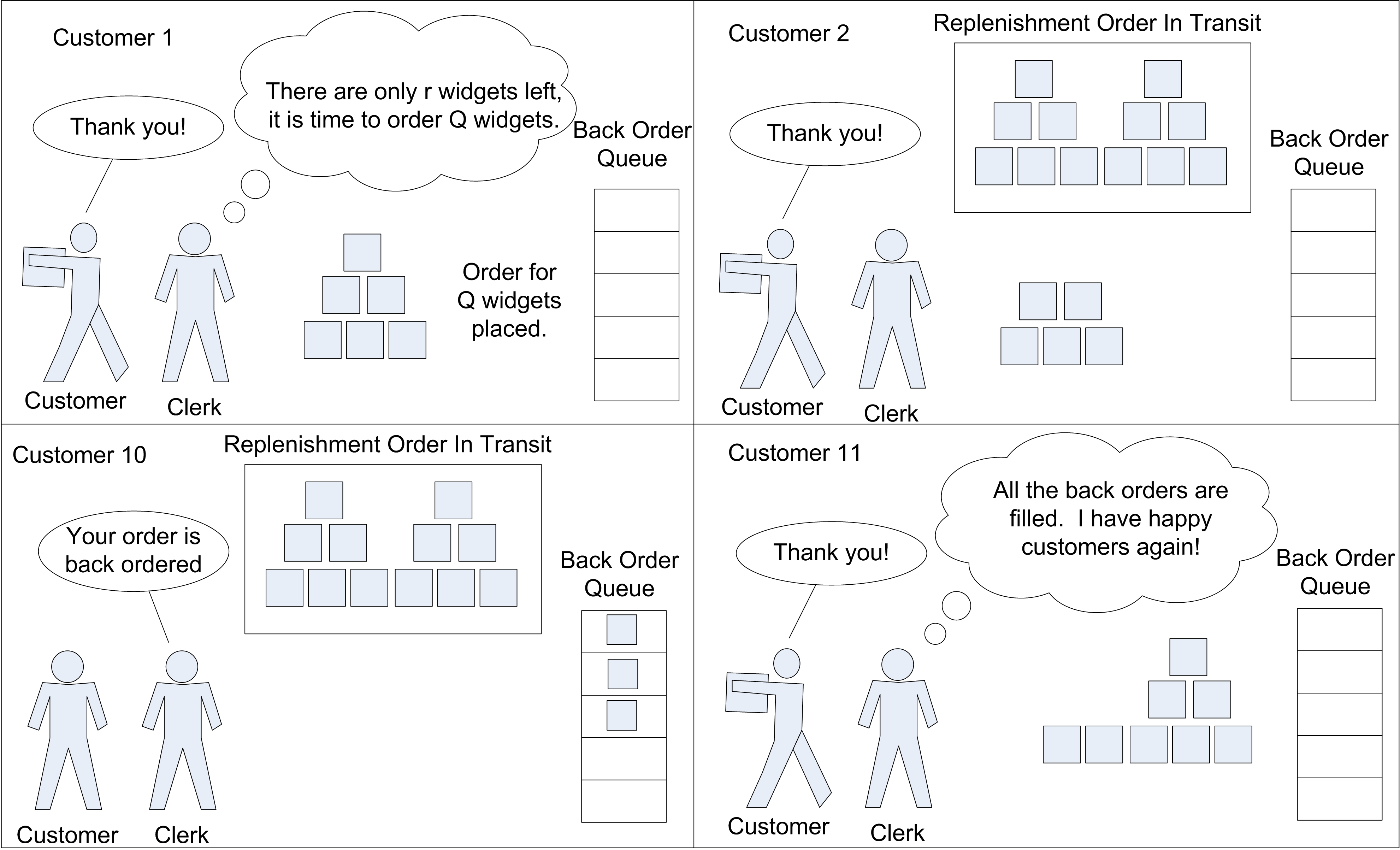
Figure 7.9: A simple reorder point, reorder quantity inventory system

There are a number of different ways to manage the replenishment process for an inventory item. These different methods are called inventory control policies. An inventory control policy must determine (at the very least) when to place a replenishment order and how much to order. This section examines the use of a reorder point (\(r\)), reorder quantity (\(Q\)) inventory policy. This is often denoted as an \((r, Q)\) inventory policy. The modeling of a number of other inventory control policies will be explored as exercises. After developing a basic understanding of how to model an \((r, Q)\) inventory system, the modeling can be expanded to study supply chains. A supply chain can be thought of as a network of locations that hold inventory in order to satisfy end customer demand.

The topic of inventory systems has been well studied. A full exposition of the topic of inventory systems is beyond the scope of this text, but the reader can consult a number of texts within the area, such as (Hadley and Whitin 1963), (Axsäter 2006), Silver, Pyke, and Peterson (1998), or (Zipkin 2000) for more details. The reader interested in supply chain modeling might consult (Nahmias 2001), (Askin and Goldberg 2002), (Chopra and Meindl 2007), or (Ballou 2004).

Within this section we will develop a model of a continuous review \((r, Q)\) inventory system with back-ordering. In a continuous review \((r, Q)\) inventory control system, demand arrives according to some stochastic process. When a demand (customer order) occurs, the amount of the demand is determined, and then the system checks for the availability of stock. If the stock on-hand is enough for the order, the demand is filled and the quantity on-hand is decreased. On the other hand, if the stock on-hand is not enough to fill the order, the entire order is back-ordered. The back-orders are accumulated in a queue and they will be filled after the arrival of a replenishment order. Assume for simplicity that the back-orders are filled on a first come first served basis. The inventory position (inventory on-hand plus on-order minus back-orders) is checked each time after a regular customer demand and the occurrence of a back-order. If the inventory position reaches or falls under the reorder point, a replenishment order is placed. The replenishment order will take a possibly random amount of time to arrive and fill any back-orders and increase the on-hand inventory. The time from when a replenishment order is placed until the time that it arrives to fill any back-orders is often called the lead time for the item.

There are three key state variables that are required to model this situation. Let \(I(t)\), \(\mathit{IO}(t)\), and \(\mathit{BO}(t)\) be the amount of inventory on hand, on order, and back-ordered, respectively at time \(t\). The net inventory, \(\mathit{IN}(t) = I(t) - \mathit{BO}(t)\), represents the amount of inventory (positive or negative). Notice that if \(I(t) > 0\), then \(\mathit{BO}(t) = 0\), and that if \(\mathit{BO}(t) > 0\), then \(I(t) = 0\). These variables compose the inventory position, which is defined as:

\[\mathit{IP}(t) = I(t) + \mathit{IO}(t) - \mathit{BO}(t)\]

The inventory position represents both the current amount on hand, \(I(t)\), the amounted back ordered, \(\mathit{BO}(t)\), and the amount previously ordered, \(\mathit{IO}(t)\). Thus, when placing an order, the inventory position can be used to determine whether or not a replenishment order needs to be placed. Since, \(\mathit{IO}(t)\), is included in \(\mathit{IP}(t)\), the system will only order, when outstanding orders are not enough to get \(\mathit{IP}(t)\) above the reorder point.

In the continuous review \((r, Q)\) policy, the inventory position must be checked against the reorder point as demands arrive to be filled. After filling (or back-ordering) a demand, either \(I(t)\) or \(\mathit{BO}(t)\) will have changed (and thus \(\mathit{IP}(t)\) will change). If \(\mathit{IP}(t)\) changes, it must be checked against the reorder point. If \(\mathit{IP}(t) \leq r\), then an order for the amount \(Q\) is placed.

The key performance measures for this type of system are the average amount of inventory on hand, the average amount of inventory back-ordered, the percentage of time that the system is out of stock, and the average number of orders made per unit time.

Let’s discuss these performance measures before indicating how to collect them within a simulation. The average inventory on hand and the average amount of inventory back-ordered can be defined as follows:

\[\begin{aligned} \bar{I} & = \frac{1}{T}\int_0^T I(t)\mathrm{d}t \\ \overline{\mathit{BO}} & = \frac{1}{T}\int_0^T \mathit{BO}(t)\mathrm{d}t\end{aligned}\]

As can be seen from the definitions, both \(I(t)\) and \(\mathit{BO}(t)\) are time-persistent variables and their averages are time averages. Under certain conditions as \(T\) goes to infinity, these time averages will converge to the steady state performance for the \((r, Q)\) inventory model. The percentage of time that the system is out of stock can be defined based on \(I(t)\) as follows:

\[SO(t) = \begin{cases} 1 & I(t) = 0\\ 0 & I(t) > 0 \end{cases}\]

\[\overline{\mathit{SO}} = \frac{1}{T}\int_0^T \mathit{SO}(t)\mathrm{d}t\]

Thus, the variable \(SO(t)\) indicates whether or not there is no stock on hand at any time. A time average value for this variable can also be defined and interpreted as the percentage of time that the system is out of stock. One minus \(\overline{\mathit{SO}}\) can be interpreted as the proportion of time that the system has stock on hand. Under certain conditions (but not always), this can also be interpreted as the fill rate of the system (i.e. the fraction of demands that can be filled immediately). Let \(Y_i\) be an indicator variable that indicates 1 if the \(i^{th}\) demand is immediately filled (without back ordering) and 0 if the \(i^{th}\) demand is back ordered upon arrival. Then, the fill rate is defined as follows.

\[\overline{\mathit{FR}} = \frac{1}{n} \sum_{i=1}^{n} Y_i\]

Thus, the fill rate is just the average number of demands that are directly satisfied from on hand inventory. The variables \(\overline{\mathit{SO}}\) and \(\overline{\mathit{FR}}\) are measures of customer service.

To understand the cost of operating the inventory policy, the average number of replenishment orders made per unit time or the average order frequency needs to be measured. Let \(N(t)\) be the number of replenishment orders placed in \((0,t]\), then the average order frequency over the period \((0,t]\) can be defined as:

\[\overline{\mathit{OF}} = \frac{N(T)}{T}\]

Notice that the average order frequency is a rate (units/time).

In order to determine the best settings of the reorder point and reorder quantity, we need an objective function that trades-off the key performance measures within the system. This can be achieved by developing a total cost equation on a per time period basis. Let \(h\) be the holding cost for the item in terms of $/unit/time. That is, for every unit of inventory held, we accrue \(h\) dollars per time period. Let \(b\) be the back order cost for the item in terms of $/unit/time. That is, for every unit of inventory back ordered, we accrue \(b\) dollars per time period. finally, let \(k\) represent the cost in dollars per order whenever an order is placed. The settings of the reorder point and reorder quantity depend on these cost factors. For example, if the cost per order is very high, then we should not want to order very often. However, this means that we would need to carry a lot of inventory to prevent a high chance of stocking out. If we carry more inventory, then the inventory holding cost is high.

The average total cost per time period can be formulated as follows:

\[\overline{\mathit{TC}} = k\overline{\mathit{OF}} + h\bar{I} + b\overline{\mathit{BO}}\]

A discussion of the technical issues and analytical results related to these variables can be found in Chapter 6 of (Zipkin 2000). Let’s take a look at an example that illustrates an inventory situation and simulates it using the KSL.

Example 7.9 (Reorder Point, Reorder Quantity Inventory Model) An inventory manager is interested in understanding the cost and service trade-offs related to the inventory management of computer printers. Suppose customer demand occurs according to a Poisson process at a rate of 3.6 units per month and the lead time is 0.5 months. The manager has estimated that the holding cost for the item is approximately $0.25 per unit per month. In addition, when a back-order occurs, the estimate cost will be $1.75 per unit per month. Every time that an order is placed, it costs approximately $0.15 to prepare and process the order. The inventory manager has set the reorder point to 1 units and the reorder quantity to 2 units. Develop a simulation model that estimates the following quantities:

  1. Average inventory on hand and back ordered

  2. Average frequency at which orders are placed

  3. Probability that an arriving customer does not have their demand immediately filled.

The examples associated with this chapter provide for a framework to model this kind of situation as well as to expand to model other inventory policies. We start the modeling by first defining an interface to represent something that can fill demand.

interface InventoryFillerIfc {
    /**
     * Represents an arrival of demand to be provided by the filler
     *
     * @param demand
     */
    fun fillInventory(demand: Int)
}

Then, we implement an abstract base class to represent different kinds of inventory situations. The class Inventory represents the key state variables of on-hand, on-order, and amount back ordered as time weighted response variables. The class requires the specification of the initial amount of inventory on-hand and a reference to an instance of an class that implements the InventoryFillerIfc interface. This instance is responsible for resupplying the inventory when it places a replenishment order.

abstract class Inventory(parent: ModelElement, initialOnHand: Int = 1, replenisher: InventoryFillerIfc, name: String?) :
    ModelElement(parent, name), InventoryFillerIfc {

    var replenishmentFiller: InventoryFillerIfc = replenisher

    protected val myAmountBackOrdered = TWResponse(this, "${this.name}:AmountBackOrdered")
    val amountBackOrdered: Int
        get() = myAmountBackOrdered.value.toInt()

    protected val myOnOrder = TWResponse(this, "${this.name}:OnOrder")
    val onOrder: Int
        get() = myOnOrder.value.toInt()

    protected val myOnHand = TWResponse(this, theInitialValue = initialOnHand.toDouble(), name = "${this.name}:OnHand")
    val onHand: Int
        get() = myOnHand.value.toInt()

    fun setInitialOnHand(amount: Int){
        require(amount>= 0) {"The initial amount on hand must be >= 0"}
        myOnHand.initialValue = amount.toDouble()
    }

The base class also defines some additional responses and a queue to hold demands that must be back ordered because they cannot be immediately filled from stock on-hand. Then, it defines three abstract methods that must be implemented by sub-classes. There must be a way to define the initial policy parameters of the inventory control policy, a method for placing replenishment orders, and a method to check the inventory position.

    val onHandResponse: TWResponseCIfc
        get() = myOnHand

    init {
        myOnHand.attachIndicator({ x -> x > 0 }, name = "${this.name}:PTimeWithStockOnHand")
    }

    val inventoryPosition: Int
        get() = onHand + onOrder - amountBackOrdered

    protected val myBackOrderQ: Queue<Demand> = Queue(this, "${this.name}:BackOrderQ")
    protected val myFirstFillRate = Response(this, "${this.name}:FillRate")

    inner class Demand(val originalAmount: Int = 1, var amountNeeded: Int) : QObject()

    abstract fun setInitialPolicyParameters(param: DoubleArray)

    abstract fun replenishmentArrival(orderAmount: Int)

    protected abstract fun checkInventoryPosition()

The base class defines what must happen to fill a demand, how to back order demand, and how to fill waiting back orders. The following code presents the default implementations. The fill demand method implements what happens when demand is fully filled. The back order demand method indicates what should be done for the amount that must be back ordered.

    protected open fun fillDemand(demand: Int) {
        myFirstFillRate.value = 1.0
        myOnHand.decrement(demand.toDouble())
    }

    protected open fun backOrderDemand(demand: Int) {
        myFirstFillRate.value = 0.0
        // determine amount to be back ordered
        val amtBO: Int = demand - onHand
        // determine the amount to give
        val amtFilled: Int = onHand
        // give all that can be given
        myOnHand.decrement(amtFilled.toDouble())
        myAmountBackOrdered.increment(amtBO.toDouble())
        // create a demand for the back order queue
        val d = Demand(demand, amtBO)
        myBackOrderQ.enqueue(d)
    }

The fillBackOrders() method can be called after a replenishment order comes in to fill requests that are waiting for inventory. In the default implementation, the amount to fill is determined and it is allocated to the waiting demand. If the demand is filled in full, it is removed from the queue; otherwise, its amount needed is reduced and it continues to wait.


    protected open fun fillBackOrders() {
        var amtToFill: Int = minOf(amountBackOrdered, onHand)
        myAmountBackOrdered.decrement(amtToFill.toDouble())
        myOnHand.decrement(amtToFill.toDouble())
        // now we have to give the amount to those waiting in the backlog queue
        // we assume filling is from first waiting until all of amtToFill is used
        while (myBackOrderQ.isNotEmpty) {
            val d = myBackOrderQ.peekNext()!!
            if (amtToFill >= d.amountNeeded) {
                amtToFill = amtToFill - d.amountNeeded
                d.amountNeeded = 0
                myBackOrderQ.removeNext()
            } else {
                d.amountNeeded = d.amountNeeded - amtToFill
                amtToFill = 0
            }
            if (amtToFill == 0) {
                break
            }
        }
    }

    protected open fun requestReplenishment(orderAmt: Int) {
        myOnOrder.increment(orderAmt.toDouble())
        replenishmentFiller.fillInventory(orderAmt)
    }

Finally, the requestReplenishment() method increments the amount on order and calls the registered replenishment filler to fill the order. Thus, an instance of Inventory acts like a filler of inventory via its implementation of the InventoryFillerIfc interface and the fact that it uses an instance of such a class to meet its own replenishment requirements. Now, we are ready to explore the concrete implementation for the reorder point, reorder quantity inventory policy situation. This is implemented within the RQInventory class.

class RQInventory(
    parent: ModelElement,
    reOrderPoint: Int = 1,
    reOrderQuantity: Int = 1,
    initialOnHand : Int = reOrderPoint + reOrderQuantity,
    replenisher: InventoryFillerIfc,
    name: String?
) : Inventory(parent, initialOnHand, replenisher, name){

    init {
        require(reOrderQuantity > 0) {"The reorder quantity must be > 0"}
        require(reOrderPoint >= -reOrderQuantity){"reorder point ($reOrderPoint) must be >= - reorder quantity ($reOrderQuantity)"}
    }

    private var myInitialReorderPt = reOrderPoint

    private var myInitialReorderQty = reOrderQuantity

    private var myReorderPt = myInitialReorderPt

    private var myReorderQty = myInitialReorderQty

    fun setInitialPolicyParameters(reorderPt: Int = myInitialReorderPt, reorderQty: Int = myInitialReorderQty) {
        require(reorderQty > 0) { "reorder quantity must be > 0" }
        require(reorderPt >= -reorderQty) { "reorder point must be >= - reorder quantity" }
        myInitialReorderPt = reorderPt
        myInitialReorderQty = reorderQty
    }

    override fun setInitialPolicyParameters(param: DoubleArray) {
        require(param.size == 2) { "There must be 2 parameters" }
        setInitialPolicyParameters(param[0].toInt(), param[1].toInt())
    }

Notice that the constructor for the class requires the reorder point and reorder quantity parameters and provides for the setting of the parameters. The class is a subclass of Inventory, which is a subclass of ModelElement. We need to have an initialize() method. Notice that the initialization resets the reorder point and reorder quantity and checks the inventory position. The check of the inventory position is required because the inventory on-hand at the start of the replication might trigger the need for a replenishment at time 0.0.

    override fun initialize() {
        super.initialize()
        myReorderPt = myInitialReorderPt
        myReorderQty = myInitialReorderQty
        checkInventoryPosition()
    }

To fill the inventory, we simply need to check if the amount on hand is sufficient, if so, the amount is filled, if not the amount to back order is determined. Because the filling of demand or the back ordering of demand may cause the change of the inventory position, the inventory position must be checked to see if a replenishment is required.

    override fun fillInventory(demand: Int) {
        require(demand > 0) { "arriving demand must be > 0" }
        if (onHand >= demand) { // fully filled
            fillDemand(demand)
        } else { // some is back ordered
            backOrderDemand(demand)
        }
        checkInventoryPosition()
    }

The check of the inventory position for a \((r, q)\) inventory policy checks to see if the inventory position has falled below the reorder point, \(r\), and if so, an order must be placed. Because the amount below the reorder point may be large due to random demand, batch multiples of the reorder quantity may be required to be ordered in order to get above the reorder position.

    override fun checkInventoryPosition() {
         if (inventoryPosition <= myReorderPt) {
            // determine the amount to order and request the replenishment
            // need to place an order, figure out the amount below reorder point
            if (inventoryPosition == myReorderPt) { // hit reorder point exactly
                requestReplenishment(myReorderQty)
            } else {
                val gap = (myReorderPt - inventoryPosition).toDouble()
                // find number of batches to order
                val n = ceil(gap / myReorderQty).toInt()
                requestReplenishment(n * myReorderQty)
            }
        }
    }

The requestReplenishment method is used to place the order. When the replenishment order arrives, we must increase the amount on-hand, decrease the amount ordered, and process any back ordered demand.

    override fun replenishmentArrival(orderAmount: Int) {
        myOnOrder.decrement(orderAmount.toDouble())
        myOnHand.increment(orderAmount.toDouble())
        // need to fill any back orders
        if (amountBackOrdered > 0) { // back orders to fill
            fillBackOrders()
        }
        checkInventoryPosition()
    }

Now we are ready to model the inventory situation described in the problem. In the following code, we encapsulate the problem within a class called RQInventorySystem. The key aspects of this model are the use of an event generator to generate the demand and the use of an inner class to provide a warehouse to fill the replenishment orders.

class RQInventorySystem(
    parent: ModelElement,
    reorderPt: Int = 1,
    reorderQty: Int = 1,
    name: String? = null
) : ModelElement(parent, name) {

    private var leadTimeRV = RandomVariable(this, ConstantRV(10.0))
    val leadTime: RandomSourceCIfc
        get() = leadTimeRV

    private var timeBetweenDemand: RandomVariable = RandomVariable(parent, ExponentialRV(365.0 / 14.0))
    val timeBetweenDemandRV: RandomSourceCIfc
        get() = timeBetweenDemand

    private val demandGenerator = EventGenerator(this, this::sendDemand, timeBetweenDemand, timeBetweenDemand)

    private val inventory: RQInventory = RQInventory(
        this, reorderPt, reorderQty, replenisher = Warehouse(), name = "Item"
    )

    fun setInitialOnHand(amount: Int){
        inventory.setInitialOnHand(amount)
    }

    fun setInitialPolicyParameters(reorderPt: Int, reorderQty: Int){
        inventory.setInitialPolicyParameters(reorderPt, reorderQty)
    }

    private fun sendDemand(generator: EventGenerator) {
        inventory.fillInventory(1)
    }

    inner class Warehouse : InventoryFillerIfc {
        override fun fillInventory(demand: Int) {
            schedule(this::endLeadTimeAction, leadTimeRV, message = demand)
        }

        private fun endLeadTimeAction(event: KSLEvent<Int>) {
            inventory.replenishmentArrival(event.message!!)
        }
    }
}

The implementation of the warehouse simply schedules a delay to represent the lead time and then calls the inventory with the amount of the replenishment after the lead time interval. In this implementation, we assume that the demand occurs in units of one. The exercises will ask the reader to generalize on this situation. Finally, we create an instance that represents the problem and perform the simulation.

fun main() {
    val m = Model()
    val reorderPoint = 1
    val reorderQty = 2
    val rqModel = RQInventorySystem(m, reorderPoint, reorderQty, "RQ Inventory Model")
    rqModel.initialOnHand = 0
    rqModel.timeBetweenDemand.initialRandomSource = ExponentialRV(1.0 / 3.6)
    rqModel.leadTime.initialRandomSource = ConstantRV(0.5)

    m.lengthOfReplication = 110000.0
    m.lengthOfReplicationWarmUp = 10000.0
    m.numberOfReplications = 40
    m.simulate()
    m.print()
    val r = m.simulationReporter
    val out = m.outputDirectory.createPrintWriter("R-Q Inventory Results.md")
    r.writeHalfWidthSummaryReportAsMarkDown(out, df = MarkDown.D3FORMAT)
}

The results for this simulation match the theoretical expected analytical results for this situation.

Inventory Model Statistical Summary Report

Name Count Average Half-Width
RQ Inventory Model:Item:OnHand 40 1.804 0.001
RQ Inventory Model:Item:PTimeWithStockOnHand 40 0.72 0
RQ Inventory Model:Item:AmountBackOrdered 40 0.104 0
RQ Inventory Model:Item:OnOrder 40 1.801 0.001
RQ Inventory Model:Item:BackOrderQ:NumInQ 40 0.104 0
RQ Inventory Model:Item:BackOrderQ:TimeInQ 40 0.153 0
RQ Inventory Model:Item:FillRate 40 0.811 0
RQ Inventory Model:Item:OrderingFrequency 40 1.801 0.001
RQ Inventory Model:Item:TotalCost 40 3.709 0.001
RQ Inventory Model:Item:OrderingCost 40 1.801 0.001
RQ Inventory Model:Item:HoldingCost 40 1.804 0.001
RQ Inventory Model:Item:BackorderCost 40 0.104 0
RQ Inventory Model:Item:NumReplenishmentOrders 40 180060.8 100.105

This example should give you a solid basis for developing more sophisticated inventory models. While analytical results are available for this example, small changes in the assumptions necessitate the need for simulation. For example, what if the lead times are stochastic or the demand is not in units of 1. In the latter case, the filling of the back-order queue should be done in different ways. For example, suppose customers wanting 5 and 3 items respectively were waiting in the queue. Now suppose a replenishment of 4 items comes in. Do you give 4 units of the item to the customer wanting 5 units (partial fill) or do you choose the customer wanting 3 units and fill their entire back-order and give only 1 unit to the customer wanting 5 units. The more realism needed, the less analytical models can be applied, and the more simulation becomes useful.

G References

Askin, R. G., and J. B. Goldberg. 2002. Design and Analysis of Lean Production Systems. John Wiley & Sons.
Axsäter, S. 2006. Inventory Control. Springer Science + Business Media.
Ballou, R. H. 2004. Business Logistics/Supply Chain Management: Planning, Organizing, and Controlling the Supply Chain. 5th ed. Prentice-Hall.
Chopra, S., and Meindl. 2007. Supply Chain Management: Strategy, Planning, and Operations. 3rd ed. Prentice-Hall.
Hadley, G., and T. M. Whitin. 1963. Analysis of Inventory Systems. Prentice Hall.
Nahmias, S. 2001. Production and Operations Analysis. 4th ed. McGraw-Hill.
Silver, E. A., D. F. Pyke, and R. Peterson. 1998. Inventory Management and Production Planning and Scheduling. 3rd ed. John Wiley & Sons.
Zipkin, P. H. 2000. Foundations of Inventory Management. McGraw-Hill.