6.5 Modeling a STEM Career Mixer
In this section, we model the operation of a STEM Career Fair mixer during a six-hour time period. The purpose of the example is to illustrate the following concepts:
Probabilistic flow of entities
Collecting statistics on observational (tally) and time-persistent data using the KSL responses
Using the
seize(),delay(),andrelease()functions of theKSLProcessBuilderclass
Example 6.8 (STEM Career Mixer System) Students arrive to a STEM career mixer event according to a Poisson process at a rate of 0.5 student per minute. The students first go to the name tag station, where it takes between 15 and 45 seconds uniformly distributed to write their name and affix the tag to themselves. We assume that there is plenty of space at the tag station, as well has plenty of tags and markers, such that a queue never forms.
After getting a name tag, 50% of the students wander aimlessly around, chatting and laughing with their friends until they get tired of wandering. The time for aimless students to wander around is triangularly distributed with a minimum of 15 minutes, a most likely value of 20 minutes, and a maximum value of 45 minutes. After wandering aimlessly, 90% decide to buckle down and visit companies and the remaining 10% just are too tired or timid and just leave. Those that decide to buckle down visit the MalWart station and then the JHBunt station as described next.
The remaining 50% of the original, newly arriving students (call them non-aimless students), first visit the MalWart company station where there are 2 recruiters taking resumes and chatting with applicants. At the MalWart station, the student waits in a single line (first come first served) for 1 of the 2 recruiters. After getting 1 of the 2 recruiters, the student and recruiter chat about the opportunities at MalWart. The time that the student and recruiter interact is exponentially distributed with a mean of 3 minutes. After visiting the MalWart station, the student moves to the JHBunt company station, which is staffed by 3 recruiters. Again, the students form a single line and pick the next available recruiter. The time that the student and recruiter interact at the JHBunt station is also exponentially distribution, but with a mean of 6 minutes. After visiting the JHBunt station, the student departs the mixer.
The organizer of the mixer is interested in collecting statistics on the following quantities within the model:
number of students attending the mixer at any time t
number of students wandering at any time t
utilization of the recruiters at the MalWart station
utilization of the recruiters at the JHBunt station
number of students waiting at the MalWart station
number of students waiting at the JHBunt station
the waiting time of students waiting at the MalWart station
the waiting time of students waiting at the JHBunt station
total time students spend at the mixer broken down in the following manner
all students regardless of what they do and when they leave
students that wander and then visit recruiters
students that do not wander
The STEM mixer organizer is interested in estimating the average time students spend at the mixer (regardless of what they do).
6.5.1 Conceptualizing the System
When developing a simulation model, whether you are an experienced analyst or a novice, you should follow a modeling recipe. I recommend developing answers to the following questions:
What is the system?
What are the elements of the system?
What information is known by the system?
What are the required performance measures?
What are the entity types?
What information must be recorded or remembered for each entity instance?
How are entities (entity instances) introduced into the system?
What are the resources that are used by the entity types?
- Which entity types use which resources and how?
What are the process flows? Sketch the process or make an activity flow diagram
Develop pseudo-code for the situation
Implement the model
We will apply each of these questions to the STEM mixer example. The first set of questions: What is the system? What information is known by the system? are used to understand what should be included in the modeling and what should not be included. In addition, understanding the system to be modeled is essential for validating your simulation model. If you have not clearly defined what you are modeling (i. e. the system), you will have a very difficult time validating your simulation model.
The first thing that I try to do when attempting to understand the system is to draw a picture. A hand drawn picture or sketch of the system to be modeled is useful for a variety of reasons. First, a drawing attempts to put down “on paper” what is in your head. This aids in making the modeling more concrete and it aids in communicating with system stakeholders. In fact, a group stakeholder meeting where the group draws the system on a shared whiteboard helps to identify important system elements to include in the model, fosters a shared understanding, and facilitates model acceptance by the potential end-users and decision makers.
You might be thinking that the system is too complex to sketch or that it is impossible to capture all the elements of the system within a drawing. Well, you are probably correct, but drawing an idealized version of the system helps modelers to understand that you do not have to model reality to get good answers. That is, drawing helps to abstract out the important and essential elements that need to be modeled. In addition, you might think, why not take some photographs of the system instead of drawing? I say, go ahead, and take photographs. I say, find some blueprints or other helpful artifacts that represent the system and its components. These kinds of things can be very helpful if the system or process already exists. However, do not stop at photographs, drawing facilitates free flowing ideas, and it is an active/engaging process. Do not be afraid to draw. The art of abstraction is essential to good modeling practice.
Alright, have I convinced you to make a drawing? So, your next question is, what should my drawing look like and what are the rules for making a drawing? Really? My response to those kinds of questions is that you have not really bought into the benefits of drawing and are looking for reasons to not do it. There are no concrete rules for drawing a picture of the system. I like to suggest that the drawing can be like one of your famous kindergarten pictures you used to share with your grandparents. In fact, if your grandparents could look at the drawing and be able to describe back to you what you will be simulating, you will be on the right track! There are not really any rules.
Well, I will take that back. I have one rule. The drawing should not look like an engineer drew it. Try not to use engineering shapes, geometric shapes, finely drawn arrows, etc. You are not trying to make a blueprint. You are not trying to reproduce the reality of the system by drawing it to perfect scale. You are attempting to conceptualize the system in a form that facilitates communication. Don’t be afraid to put some labels and text on the drawing. Make the drawing a picture that is rich in the elements that are in the system. Also, the drawing does not have to be perfect, and it does not have to be complete. Embrace the fact that you may have to circle back and iterate on the drawing as new modeling issues arise. You have made an excellent drawing if another simulation analyst could take your drawing and write a useful narrative description of what you are modeling.
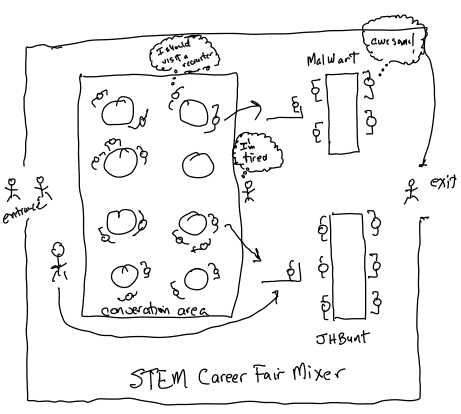
Figure 6.12: Rich picture system drawing of STEM Career Mixer
Figure 6.12 illustrates a drawing for the STEM mixer problem. As you can see in the drawing, we have students arriving to a room that contains some tables for conversation between attendees. In addition, the two company stations are denoted with the recruiters and the waiting students. We also see the wandering students and the timid students’ paths through the system. At this point, we have a narrative description of the system (via the problem statement) and a useful drawing of the system. We are ready to answer the following questions:
What are the elements of the system?
What information is known by the system?
When answering the question “what are the elements?”, your focus should be on two things: 1) the concrete structural things/objects that are required for the system to operate and 2) the things that are operated on by the system (i.e. the things that flow through the system).
What are the elements?
students (non-wanderers, wanderers, timid)
recruiters: 2 for MalWart and 3 for JHBunt
waiting lines: one line for MalWart recruiters, one line for JHBunt recruiters
company stations: MalWart and JHBunt
The paths that students may take.
Notice that the answers to this question are mostly things that we can point at within our picture (or the real system).
When answering the question “what information is known at the system level?”, your focus should be identifying facts, input parameters, and environmental parameters. Facts tend to relate to specific elements identified by the previous question. Input parameters are key variables, distributions, etc. that are typically under the control of the analyst and might likely be varied during the use of the model. Environmental parameters are also a kind of input parameter, but they are less likely to be varied by the modeler because they represent the operating environment of the system that is most likely not under control of the analyst to change. However, do not get hung up on the distinction between input parameters and environmental parameters, because their classification may change based on the objectives of the simulation modeling effort. Sometimes innovative solutions come from questioning whether or not an environmental parameter can really be changed.
What information is known at the system level?
students arrive according to a Poisson process with mean rate 0.5 students per minute or equivalently the time between arrivals is exponentially distributed with a mean of 2 minutes
time to affix a name tag ~ uniform(15, 45) seconds
50% of students are go-getters and 50% are wanderers
time to wander ~ triangular(15, 20, 45) minutes
10% of wanderers become timid/tired, 90% visit recruiters
number of MalWart recruiters = 2
time spent chatting with MalWart recruiter ~ exponential(3) minutes
number of JHBunt recruiters = 3
time spent chatting with JHBunt recruiter ~ exponential(6) minutes
A key characteristic of the answers to this question is that the information is “global”. That is, it is known at the system level. We will need to figure out how to represent the storage of this information when implementing the model within software.
The next question to address is “What are the required performance measures?“ For this situation, we have been given as part of the problem a list of possible performance measures, mostly related to time spent in the system and other standard performance measures related to queueing systems. In general, you will not be given the performance measures. Instead, you will need to interact with the stakeholders and potential users of the model to identify the metrics that they need in order to make decisions based on the model. Identifying the metrics is a key step in the modeling effort. If you are building a model of an existing system, then you can start with the metrics that stakeholders typically use to character the operating performance of the system. Typical metrics include cost, waiting time, utilization, work in process, throughput, and probability of meeting design criteria.
Once you have a list of performance measures, it is useful to think about how you would collect those statistics if you were an observer standing within the system. Let’s pretend that we need to collect the total time that a student spends at the career fair and we are standing somewhere at the actual mixer. How would you physically perform this data collection task? In order to record the total time spent by each student, you would need to note when each student arrived and when each student departed. Let \(A_{i}\) be the arrival time of the \(i^{\text{th}}\) student to arrive and let \(D_{i}\) be the departure time of the \(i^{\text{th}}\) student. Then, the system time (T) of the \(i^{\text{th}}\) student is \({T_{i} = D}_{i} - A_{i}\). How could we keep track of \(A_{i}\) for each student? One simple method would be to write the time that the student arrived on a sticky note and stick the note on the student’s back. Hey, this is pretend, right? Then, when the student leaves the mixer, you remove the sticky note from their back and look at your watch to get \(D_{i}\) and thus compute, \(T_{i}\). Easy! We will essentially do just that when implementing the collection of this statistic within the simulation model. Now, consider how you would keep track of the number of students attending the mixer. Again, standing where you can see the entrance and the exit, you would increment a counter every time a student entered and decrement the counter every time a student left. We will essentially do this within the simulation model.
Thus, identifying the performance measures to collect and how you will collect them will answer the 2nd modeling question. You should think about and document how you would do this for every key performance measure. However, you will soon realize that simulation modeling languages, like Arena, have specific constructs that automatically collect common statistical quantities such as resource utilization, queue waiting time, queue size, etc. Therefore, you should concentrate your thinking on those metrics that will not automatically be collected for you by the simulation software environment. In addition to identifying and describing the performance measures to be collected, you should attempt to classify the underlying data needed to compute the statistics as either observation-based (tally) data or time-persistent (time-weighted) data. This classification will be essential in determining the most appropriate constructs to use to capture the statistics within the simulation model. The following table summarizing the type of each performance measure requested for the STEM mixer simulation model.
| Performance Measure | Type |
|---|---|
| Average number of students attending the mixer at any time t | Time persistent |
| Average number of students wandering within the mixer at any time t | Time persistent |
| Average utilization of the recruiters at the MalWart station | Time persistent |
| Average utilization of the recruiters at the MalWart station | Time persistent |
| Average utilization of the recruiters at the JHBunt station | Time persistent |
| Average number of students waiting at the MalWart station | Time persistent |
| Average number of students waiting at the JHBunt station | Time persistent |
| Average waiting time of students waiting at the MalWart station | Tally |
| Average waiting time of students waiting at the JHBunt station | Tally |
| Average system time for students regardless of what they do | Tally |
| Average system time for students that wander and then visit recruiters | Tally |
| Average system time for students that do not wander | Tally |
Now, we are ready to answer the rest of the questions. When performing a process-oriented simulation, it is important to identify the entity types and the characteristics of their instances. An entity type is a classification or indicator that distinguishes between different entity instances. If you are familiar with object-oriented programming, then an entity type is a class, and an entity instance is an object of that class. Thus, an entity type describes the entity instances (entities) that are in its class. An entity instance (or just entity) is something that flows through the processes within the system. Entity instances (or just entities) are realizations of objects within the entity type (class). Different entity types may experience different processes within the system. The next set of questions are about understanding entity types and their instances: What are the entity types? What information must be recorded or remembered for each entity (entity instance) of each entity type? How are entities (entity instances) for each entity type introduced into the system?
Clearly, the students are a type of entity. We could think of having different sub-types of the student entity type. That is, we can conceptualize three types of students (non-wanderers, wanderers, and timid/tired). However, rather than defining three different classes or types of students, we will just characterize one general type of entity called a Student and denote the different types with an attribute that indicates the type of student. An attribute is a named property of an entity type and can have different values for different instances. We will use the attributes to indicate whether the student wanders or not and whether the wandering student leaves without visiting recruiters. Then, we will these attributes to help in determining the path that a student takes within the system and when collecting the required statistics.
We are basically told how the students (instances of the student entity type) are introduced to the system. That is, we are told that the arrival process for students is Poisson with a mean rate of 0.5 students per minute. Thus, we have that the time between arrivals is exponential with a mean of 2 minutes. What information do we need to record or be remembered for each student? The answer to this question identifies the attributes of the entity. Recall that an attribute is a named property of an entity type which can take on different values for different entity instances. Based on our conceptualization of how to collect the total time in the system for the students, it should be clear that each entity (student) needs to remember the time that the student arrived. That is our sticky note on their backs. In addition, since we need to collect statistics related to how long the different types of students spend at the STEM fair, we need each student (entity) to remember what type of student they are (non-wanderer, wanderer, and timid/tired).
After identifying the entity types, you should think about identifying the resources. Resources are system elements that entity instances need in order to proceed through the system. The lack of a resource causes an entity to wait (or block) until the resource can be obtained. By the way, if you need help identifying entity types, you should identify the things that are waiting in your system. It should be clear from the picture that students wait in either of two lines for recruiters. Thus, we have two resources: MalWart Recruiters and JHBunt Recruiters. We should also note the capacity of the resources. The capacity of a resource is the total number of units of the resource that may be used. Conceptually, the 2 MalWart recruiters are identical. There is no difference between them (as far as noted in the problem statement). Thus, the capacity of the MalWart recruiter resource is 2 units. Similarly, the JHBunt recruiter resource has a capacity of 3 units.
In order to answer the “and how” part of the question, I like to summarize the entities, resources and activities experienced by the entity types in a table. Recall that an activity is an interval of time bounded by two events. Entities experience activities as they move through the system. The following table summarizes the entity types, the activities, and the resources. This will facilitate the drawing of an activity diagram for the entity types.
| Entity Type | Activity | Resource Used |
|---|---|---|
| Student (all) | time to affix a name tag ~ UNIF(15, 45) seconds | None |
| Student (wanderer) | Wandering time ~ TRIA(15, 15, 45) minutes | None |
| Student (not timid) | Talk with MalWart ~ EXPO(3) minutes | 1 of the 2 MalWart recruiters |
| Student (not timid) | Talk with JHBunt ~ EXPO(6) minutes | 1 of the 3 JHBunt recruiters |
Now we are ready to document the processes experienced by the entities. A good way to do this is through an activity flow diagram. As previously described, an activity diagram will have boxes that show the activities, circles to show the queues and resources, and arrows, to show the paths taken. Figure 6.13 presents the activity diagram for this situation.
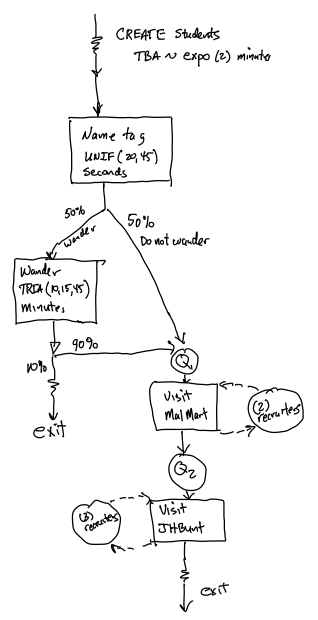
Figure 6.13: Activity diagram for STEM Career Mixer
In Figure 6.13, we see that the students are created according to a time between arrival (TBA) process that is exponentially distributed with a mean of 2 minutes and they immediately experience the activity associated with affixing the name tag. Note that the activity does not require any resources and thus has no queue in front of it. Then, the students follow one of two paths, with 50% becoming “non-wanderers” and 50% becoming “wanderers”. The wandering students, wander aimlessly, for period of time, which is represented by another activity that does not require any resources. Then, the 90% of the students follow the non-wanderer path and the remaining 10% of the students, the timid/tired students, leave the system. The students that decide to visit the recruiting stations, first visit the MalWart station, where in the diagram we see that there is an activity box for their talking time with the recruiter. During this talking time, they require one of the recruiters and thus we have a resource circle indicating the usage of the resource. In addition, we have a circle with a queue denoted before the activity to indicate that the students visiting the station may need to wait. The JHBunt station is represented in the same fashion. After visiting the JHBunt station, the students depart the mixer. Now, we are ready to represent to start representing this system in KSL code.
6.5.2 Implementing the STEM Mixer Model
The first thing that should be done is to prepare to use a process model by defining the model element that will contain the system. So, we start the modeling by defining a class that is a subclass of ProcessModel:
We will place the model elements needed within this class. We have already identified the need for many random variables. So, let’s add those next.
class StemFairMixer(
parent: ModelElement,
name: String? = null
) : ProcessModel(parent, name) {
private val myTBArrivals: RVariableIfc = ExponentialRV(2.0, 1)
private val myNameTagTimeRV = RandomVariable(this, UniformRV((15.0/60.0), (45.0/60.0), 2))
private val myWanderingTimeRV = RandomVariable(this, TriangularRV(15.0, 20.0, 45.0, 3),
name = "WanderingT")
private val myTalkWithJHBunt = RandomVariable(this, ExponentialRV(6.0, 4))
private val myTalkWithMalMart = RandomVariable(this, ExponentialRV(3.0, 5))
private val myDecideToWander = RandomVariable(this, BernoulliRV(0.5, 6))
private val myDecideToLeave = RandomVariable(this, BernoulliRV(0.1, 7))Notice that I have converted the time for performing the name tag activity to minutes and that all other time units are in minutes. Also, the random variables have specific stream numbers specified.
We know that we need to collect statistics. So, using the KSL Response and TWResponse classes these KSL constructs can be added next.
class StemFairMixer(
parent: ModelElement,
name: String? = null
) : ProcessModel(parent, name) {
private val myTBArrivals: RVariableIfc = ExponentialRV(2.0, 1)
private val myNameTagTimeRV = RandomVariable(this, UniformRV((15.0 / 60.0), (45.0 / 60.0), 2))
private val myWanderingTimeRV = RandomVariable(this, TriangularRV(15.0, 20.0, 45.0, 3),
name = "WanderingT")
private val myTalkWithJHBunt = RandomVariable(this, ExponentialRV(6.0, 4))
private val myTalkWithMalMart = RandomVariable(this, ExponentialRV(3.0, 5))
private val myDecideToWander = RandomVariable(this, BernoulliRV(0.5, 6))
private val myDecideToLeave = RandomVariable(this, BernoulliRV(0.1, 7))
private val myOverallSystemTime = Response(this, "OverallSystemTime")
private val mySystemTimeNW = Response(this, "NonWanderSystemTime")
private val mySystemTimeW = Response(this, "WanderSystemTime")
private val mySystemTimeL = Response(this, "LeaverSystemTime")
private val myNumInSystem = TWResponse(this, "NumInSystem")Finally, we are ready to add the elements necessary for the process model.
class StemFairMixer(
parent: ModelElement,
name: String? = null
) : ProcessModel(parent, name) {
private val myTBArrivals: RVariableIfc = ExponentialRV(2.0, 1)
private val myNameTagTimeRV = RandomVariable(this, UniformRV((15.0/60.0), (45.0/60.0), 2))
private val myWanderingTimeRV = RandomVariable(this, TriangularRV(15.0, 20.0, 45.0, 3),
name = "WanderingT")
private val myTalkWithJHBunt = RandomVariable(this, ExponentialRV(6.0, 4))
private val myTalkWithMalMart = RandomVariable(this, ExponentialRV(3.0, 5))
private val myDecideToWander = RandomVariable(this, BernoulliRV(0.5, 6))
private val myDecideToLeave = RandomVariable(this, BernoulliRV(0.1, 7))
private val myOverallSystemTime = Response(this, "OverallSystemTime")
private val mySystemTimeNW = Response(this, "NonWanderSystemTime")
private val mySystemTimeW = Response(this, "WanderSystemTime")
private val mySystemTimeL = Response(this, "LeaverSystemTime")
private val myNumInSystem = TWResponse(this, "NumInSystem")
private val myJHBuntRecruiters: ResourceWithQ = ResourceWithQ(this,
capacity = 3, name = "JHBuntR")
val jhBuntRecruiters : ResourceWithQCIfc
get() = myJHBuntRecruiters
private val myMalWartRecruiters: ResourceWithQ = ResourceWithQ(this,
capacity = 2, name = "MalWartR")
val malWartRecruiters : ResourceWithQCIfc
get() = myMalWartRecruiters
private val generator = EntityGenerator(::Student, myTBArrivals, myTBArrivals)Well, actually, we cannot really add the EntityGenerator until we have defined the class Student. This is done as an inner class of StemFairMixer. Because it is an inner class of StemFairMixer, it will have access to all the previously defined random variables, resources, and statistical responses.
In the following code, two attributes, isWanderer and isLeaver are defined as properties of Student. Notice how the values of these properties are assigned upon creation using the random variables and how the values of 1.0 or 0.0 are converted to boolean values. This is performed by using an extension function found in the ksl.utilities.random.rvariable package within the KSLRandom class file. It is very convenient for use with if statements. It is important to note that individual instances of the Student class will get different values for their isWanderer and isLeaver properties. When the object instance is created, the assignment to the property occurs. At that time, a new random value is generated, converted from 1.0 or 0.0 to true or false and then assigned to the created student object.
private inner class Student : Entity() {
private val isWanderer = myDecideToWander.value.toBoolean()
private val isLeaver = myDecideToLeave.value.toBoolean()
val stemFairProcess = process(isDefaultProcess = true) {
myNumInSystem.increment()
delay(myNameTagTimeRV)
if (isWanderer) {
delay(myWanderingTimeRV)
if (isLeaver) {
departMixer(this@Student)
return@process
}
}
val mw = seize(myMalWartRecruiters)
delay(myTalkWithMalMart)
release(mw)
val jhb = seize(myJHBuntRecruiters)
delay(myTalkWithJHBunt)
release(jhb)
departMixer(this@Student)
}The process followed by each student is defined in the process property called stemFairProcess. Notice how we first increment the number in the system and start the delay for the name tag activity. If the student is a wandering student, we experience the delay for wandering. And, if the student is a wandering student that leaves early, then the departingMixer() function is called. As we will see in a moment, this function will be used to collect statistics on departing students.
Now we have something new, we have a return statement within a process. As previously noted, Kotlin flow of control statements are available within coroutines and return is a flow of control statement. Because the return statement is within a process builder, we need to be more specific about the return label. This can be specified by the name of the builder function. In this case process. Kotlin also allows you to explicitly label the return. This return statement will cause the normal exit from the process routine for those students that leave without visiting recruiters.
The students that visit the recruiter (seize-delay-release) the related resources and then depart. The following code shows the departMixer() function. In this function, we decrement the number in the system and collect the system time statistics. Notice how we use the attributes within the boolean conditions of the if statements to get the correct system time response variables.
private fun departMixer(departingStudent: Student) {
myNumInSystem.decrement()
val st = time - departingStudent.createTime
myOverallSystemTime.value = st
if (isWanderer) {
mySystemTimeW.value = st
if (isLeaver) {
mySystemTimeL.value = st
}
} else {
mySystemTimeNW.value = st
}
}
}The results of this simulation indicate that the JHBunt recruiters have the highest utilization.
Half-Width Statistical Summary Report - Confidence Level (95.000)%
Name Count Average Half-Width
------------------------------------------------------------------------------
OverallSystemTime 400 34.3985 0.8019
NonWanderSystemTime 400 22.3367 0.8123
WanderSystemTime 400 47.1614 0.7897
LeaverSystemTime 400 27.0096 0.2321
NumInSystem 400 16.9105 0.4610
JHBuntR:InstantaneousUtil 400 0.8411 0.0065
JHBuntR:NumBusyUnits 400 2.5232 0.0195
JHBuntR:ScheduledUtil 400 0.8411 0.0065
JHBuntR:WIP 400 7.5014 0.3772
JHBuntR:Q:NumInQ 400 4.9783 0.3648
JHBuntR:Q:TimeInQ 400 10.6658 0.7411
MalWartR:InstantaneousUtil 400 0.6766 0.0071
MalWartR:NumBusyUnits 400 1.3531 0.0142
MalWartR:ScheduledUtil 400 0.6766 0.0071
MalWartR:WIP 400 2.6757 0.1209
MalWartR:Q:NumInQ 400 1.3226 0.1105
MalWartR:Q:TimeInQ 400 2.7871 0.2147
JHBuntR:SeizeCount 400 154.4125 1.0191
MalWartR:SeizeCount 400 164.1375 1.2031
------------------------------------------------------------------------------The results produced by the KSL are within statistical variation of the same system modeled with a commercial simulation language discussed in this book.