7.6 Exercises
Exercise 7.1 Consider the testing and repair shop. Suppose instead of increasing the overall arrival rate of jobs to the system, the new contract will introduce a new type of component into the system that will require a new test plan sequence. The following two tables represent the specifics associated with the new testing plan.
| Test Plan | % of parts | Sequence |
|---|---|---|
| 1 | 20% | 2,3,2,1 |
| 2 | 12.5% | 3,1 |
| 3 | 37.5% | 1,3,1 |
| 4 | 20% | 2,3 |
| 5 | 10% | 2,1,3 |
| Test Plan | Testing Time Parameters | Repair Time Parameters |
|---|---|---|
| 1 | (20,4.1), (12,4.2), (18,4.3), (16,4.0) | (30,60,80) |
| 2 | (12,4), (15,4) | (45,55,70) |
| 3 | (18,4.2), (14,4.4), (12,4.3) | (30,40,60) |
| 4 | (24,4), (30,4) | (35,65,75) |
| 5 | (20,4.1), (15,4), (12,4.2) | (20,30,40) |
Management is interested in understanding where the potential bottlenecks are in the system and in developing alternatives to mitigate those bottlenecks so that they can still handle the contract. The new contract stipulates that 80% of the time the testing and repairs should be completed within 480 minutes. The company runs 2 shifts each day for each 5 day work week. Any jobs not completed at the end of the second shift are carried over to first shift of the next working day. Assume that the contract is going to last for 1 year (52 weeks). Build a simulation model that can assist the company in assessing the risks associated with the new contract.
Use the following stream allocations:
- Stream 1, part arrival process
- Stream 2, diagnostic time
- Stream 3, test plan distribution
- Streams 4-8, test plan 1 testing times and repair
- Streams 9-11, test plan 2 testing times and repair
- Streams 12-15, test plan 3 testing times and repair
- Streams 16-18, test plan 4 testing times and repair
- Streams 19-22, test plan 5 testing times and repair
Exercise 7.2 Parts arrive at a 4 workstation system according to an exponential inter-arrival distribution with a mean of 10 minutes (stream 1). The workstation A has 2 machines. The three workstations (B, C, D) each have a single machine. There are 3 part types, each with an equal probability of arriving (stream 2). The process plan for the part types are given below. The entries are for exponential distributions with the mean processing time (MPT) parameter given.
| Workstation, MPT | Workstation, MPT | Workstation, MPT |
| A, 9.5 | C, 14.1 | B, 15 |
| A, 13.5 | B, 15 | C, 8.5 |
| A, 12.6 | B, 11.4 | D, 9.0 |
Assume that the transfer time between arrival and the first station, between all stations, and between the last station and the system exit is 3 minutes (stream 3). Simulate the system for 30000 minutes and discuss the potential bottlenecks in the system.
Use the following stream allocations for the process plans:
- Streams 4-6, Plan 1
- Streams 7-9, Plan 2
- Streams 10-12, Plan 3
Exercise 7.3 A small manufacturing system produces three types of parts. There is a 30% chance of getting a Type 1 part, a 50% chance of getting a Type 2 part and a 20% chance of getting a Type 3 part. The parts arrive from an upstream process such that the time between arrivals is exponentially distributed with a mean of 3 minutes. All parts that enter the system must go through a preparation station where there are 2 preparation workers. The preparation time is exponentially distributed with means 3, 5, and 7 for part types 1, 2, and 3, respectively.
There is only space for 6 parts in the preparation queue. Any parts that that arrive to the system when there are 6 or more parts in the preparation queue cannot enter the system. These parts are shunted to a re-circulating conveyor, which takes 10 minutes to re-circulate the parts before they can try again to enter the preparation queue. Hint: Model the re-circulating conveyor as a simple deterministic delay.
After preparation, the parts are processed on two different production lines. A production line is dedicated to type 1 parts and a production line is dedicated to type 2 and 3 parts. Part types 2 and 3 are built one at a time on their line by 1 of 4 operators assigned to the build station. The time to build a part type 2 or 3 part is triangularly distributed with a (min = 5, mode = 10, max = 15) minutes. After the parts are built they leave the system.
Part type 1 has a more complicated process because of some special tooling that is required during the build process. In addition, the build process is separated into two different operations. Before starting operation 1, the part must have 1 of 10 special tooling fixtures. It takes between 1 and 2 minutes uniformly distributed to place the part in the tooling fixture. An automated machine places the part in the tooling so that the operator at operation 1 does not have to handle the part. There is a single operator at operation 1 which takes 3 minutes on average exponentially distributed. The part remains in the tooling fixture after the first operation and proceeds to the second operation. There is 1 operator at the second operation which takes between 3 and 6 minutes uniformly distributed. After the second operation is complete, the part must be removed from the tooling fixture. An automated machine removes the part from the tooling so that the operator at operation 2 does not have to handle the part. It takes between 20 and 30 seconds uniformly distributed to remove the part from the tooling fixture. After the part is built, it leaves the system.
In this problem, the steady state performance of this system is required in order to identify potential long-term bottlenecks in this process. For this analysis, collect statistics on the following quantities:
Queue statistics for all stations. Utilization statistics for all resources.
The system time of parts by part type. The system time should not include the time spent on the re-circulating conveyor.
The average number of parts on the conveyor.
Perform a warm up analysis on the system time of a part regardless of type.
Use the following stream allocations:
- Stream 1, part type distribution
- Stream 2, arrival process
- Streams 3-5, preparation time for types 1, 2, 3
- Stream 6, part type 2 or 3 build time
- Stream 7, part type 1 tooling placement time
- Stream 8, part type 1 first operation time
- Stream 9, part type 1 second operation time
- Stream 10, part type 1, tooling removal time
Exercise 7.4 Reconsider Exercise 7.3. A process change is being recommended for the build station for part type 2 and 3. In particular, a machine change will cause the processing time to be log-normally distributed with a mean of 10 and a standard deviation of 2 minutes. Compare the system time of the old configuration and the new configuration based on 30 replications of length 1000 hours with a warm up of 200 hours. Which configuration would you recommend?
Exercise 7.5 A patient arrives at the Emergency Room about every 20 \(\pm\) 10 minutes (stream 1). The notation X \(\pm\) Y means uniformly distributed with minimum \(X-Y\) and maximum \(X+Y\). They will be treated by either of two doctors.
Twenty percent of the patients are classified as NIA (need immediate attention) and the rest as CW (can wait). NIA patients are given the highest priority, 3, see a doctor as soon as possible for 40 \(\pm\) 37 minutes (stream 2), then have their priority reduced to 2 and wait until a doctor is free again, when they receive further treatment for 30 \(\pm\) 25 minutes (stream 3) and are discharged.
CW patients initially receive a priority of 1 and are treated (when their turn comes) for 15 \(\pm\) 14 minutes (stream 4); their priority is then increased to 2, they wait again until a doctor is free, receive 10 \(\pm\) 8 minutes (stream 5) of final treatment, and are discharged.
An important aspect of this system is that patients that have already seen the doctor once compete with newly arriving patients that need a doctor. As indicated, patients who have already seen the doctor once, have a priority level of 2 (either increased from 1 to 2 or decreased from 3 to 2). Thus, there is one shared queue for the first treatment activity and the final treatment activity. In addition, we assume that the doctors are interchangeable. That is, it does not matter which of the 2 doctors performs the first or final treatment. Assume that the initial treatment activity has a higher priority over the final treatment for a doctor.
Simulate for 20 days of continuous operation, 24 hours per day. Precede this by a 2-day initialization period to load the system with patients.
Measure the average queue length of NIA patients from arrival to first seeing a doctor. What percent have to wait to see the doctor for the first treatment? Report statistics on the initial waiting time for NIA patients. What percent wait less than 5 minutes before seeing a doctor for the first time? Report statistics on the time in system for the patients. Report statistics on the remaining time in system from after the first treatment to discharge, for all patients. Discuss what changes to your model are necessary if the doctors are not interchangeable. That is, suppose there are two doctors: Dr. House and Dr. Wilson. The patient must get the same doctor for their final treatment as for their first treatment. For example, if a patient gets Dr. House for their first treatment, they must see Dr. House for their final treatment. You do not have to implement the changes.
Exercise 7.6 Consider the M/G/1 queue with the following variation. The server works continuously as long as there is at least one customer in the system. The customers are processed FIFO. When the server finishes serving a customer and finds the system empty, the server goes away for a length of time called a vacation. At the end of the vacation the server returns and begins to serve the customers, if any, who have arrived during the vacation. If the server finds no customers waiting at the end of a vacation, it immediately takes another vacation, and continues in this manner until it finds at least one waiting customer upon return from a vacation. Assume that the time between customer arrivals is exponentially distributed with mean of 3 minutes (stream 1). The service distribution for each customer is a gamma distribution with a mean of 4.5 seconds and a variance of 3.375 (stream 2). The length of a vacation is a random variable uniformly distributed between 8 and 12 minutes (stream 3).
Run the simulation long enough to adequately develop a 95% confidence interval on the expected wait time in the queue for a arbitrary customer arriving in steady state. In addition, develop an empirical distribution for the number of customers waiting upon the return of the server from vacation. In other words, estimate the probability that \(j = 0, 1, 2\), etc, where \(j\) is the number of waiting customers in the queue upon the return of the server from a vacation. This queue has many applications, for example, consider how a bus stop operates.
Exercise 7.7 An airline ticket office has two ticket agents answering incoming phone calls for flight reservations. In addition, six callers can be put on hold until one of the agents is available to take the call. If all eight phone lines (both agent lines and the hold lines) are busy, a potential customer gets a busy signal, and it is assumed that the call goes to another ticket office and that the business is lost. The calls and attempted calls occur randomly (i.e. according to Poisson process) at a mean rate of 15 per hour (stream 1). The length of a telephone conversation has an exponential distribution with a mean of 4 minutes (stream 2).
In addition, the ticket office has instituted an automated caller identification system that automatically places First Class Business (FCB) passengers at the head of the queue, waiting for an agent. Of the original 15 calls per hour, they estimate that roughly one-third of these come from FCB customers (stream 3). They have also noticed that FCB customers take approximately 3 minutes on average for the phone call, still exponentially distributed (stream 4). Regular customers still take on average 4 minutes, exponentially distributed (stream 2). Simulate this system with and without the new prioritization scheme and compare the average waiting time for the two types of customers.
Exercise 7.8 Consider a system having 6 machines tended by 2 operators. In this system, there are two types of stoppages. Type 1 stoppage occurs after a fixed constant amount of machine running time, \(1/\lambda_1\) = 30 minutes, and has a constant value of \(1/\mu_1\) = 10 minutes as the service time for the stoppage. Type 2 stoppages occur after random intervals of time, negatively exponentially distributed, with a mean of \(1/\lambda_2\) = 10 minutes (stream 1). Service times for type 2 stoppages are negative exponentially distributed with a mean of \(1/\mu_2\) = 4 minutes (stream 2). Both of the operators have the same skills and can handle either type of stoppage. The machines wait for service from the operators in a first come first served queue with no priority given to either type of stoppage. Simulate this system for 10000 minutes to estimate the average number of waiting machines by type of stoppage, the average utilization of the operator, the average utilization of the machines, and the average waiting time of the machines by type of stoppage.
Exercise 7.9 Suppose a service facility consists of two stations in series (tandem), each with its own FIFO queue. Each station consists of a queue and a single server. A customer completing service at station 1 proceeds to station 2, while a customer completing service at station 2 leaves the facility. Assume that the inter-arrival times of customers to station 1 are IID exponential random variables with a mean of 1 minute (stream 1). Service times of customers at station 1 are exponential random variables with a mean of 0.7 minute (stream 2), and at station 2 are exponential random variables with mean 0.9 minute (stream 3). Develop an model for this system.
Run the simulation for exactly 20000 minutes and estimate for each station the expected average delay in queue for the customer, the expected time-average number of customers in queue, and the expected utilization. In addition, estimate the average number of customers in the system and the average time spent in the system.
Use the results of queueing theory to verify and validate your results for part (a)
Suppose now there is a travel time from the exit of station 1 to the arrival to station 2. Assume that this travel time is distributed uniformly between 0 and 2 minutes. Modify your simulation and rerun it under the same conditions as in part (a).
Exercise 7.10 Parts arrive to a machine shop according to an exponential distribution with a mean of 10 minutes. Before the parts go into the main machining area they must be prepped. The preparation area has two preparation machines that are tended by 2 operators. Upon arrival parts are assigned to either of the two preparation machines with equal probability. Except for processing times the two preparation machines operate in the same manner. When a part enters a preparation machine area, it requires the attention of an operator to setup the part on the machine. After the machine is setup, the machine can process without the operator. Upon completion of the processing, the operator is required to remove the part from the machine. The same operator does all the setups and part removals. The operator attends to the parts in a first come, first served manner. The times for the preparation machines are given in the table below according to a triangular distribution with the provided parameters:
| Prep Machine | Setup Time | Process Time | Removal Time |
|---|---|---|---|
| 1 | (8,11,16) | (15,20,23) | (7,9,12) |
| 2 | (6,8,14) | (11,15,20) | (4,6,8) |
After preparation the parts must visit the machine shop. There are 4 machines in the machine shop. The parts follow a specific sequence of machines within the shop. This is determined after they have been prepped. The percentage for each sequence is given in the table below. The #,(min, mode, max) provides the machine number, #, and the parameters for the processing times for a triangular distribution in minutes.
| Sequence | % | #,(min, mode, max) | #,(min, mode, max) | #,(min, mode, max) | #,(min, mode, max) |
|---|---|---|---|---|---|
| 1 | 12 | 1,(10.5,11.9,13.2) | 2, (7.1,8.5,9.8) | 3,(6.7,8,10) | 4, (1,8.9,10.3) |
| 2 | 14 | 1,(7.3,8.6,10.1) | 3,(5.4,7.2, 11.3) | 2,(9.6, 11.4, 15.3) | |
| 3 | 31 | 2,(8.7,9.9,12) | 4,(8.6,10.3,12.8) | 1,(10.3, 12.4, 14.8) | 3,(8.4,9.7,11) |
| 4 | 24 | 3,(7.9,9.3, 10.9) | 4,(7.6,8.9,10.3) | 3,(6.5,8.3,9.7) | 2,(6.7,7.8,9.4) |
| 5 | 19 | 2,(5.6,7.1,8.8) | 1,(8.1, 9.4, 11.7) | 4,(9.1, 10.7, 12.8) |
The transfer time between the prep area and the first machine in the sequence, between all machines, and between the last machine and the system exit follows a triangular distribution with parameters 2, 4, 6 minutes.
Run the model for 200,000 minutes. Report average and 95% half-width statistics on the utilization of the preparation operator, the utilization of the preparation machines, the utilization of the job shop machines 1-4, number of parts in the system, and time spent in the system (in minutes).
Recommend a warm up period for the total time spent in the system. Show your work to justify your recommendation.
Where is the bottleneck for this system? What would you recommend to improve the performance of this system?
Use the following stream allocations:
- Stream 1, part arrival process
- Stream 2, preparation machine routing
- Streams 3-5, setup, preparation, removal time for prep machine 1
- Streams 6-8, setup, preparation, removal time for prep machine 2
- Stream 9, sequence determination
- Stream 10-13, sequence 1 processing times
- Stream 14-16, sequence 2 processing times
- Stream 17-20, sequence 3 processing times
- Stream 21-24, sequence 4 processing times
- Stream 25-27, sequence 5 processing times
- Stream 28, transfer time
Exercise 7.11 Consider the simple three-workstation flow line. Parts entering the system are placed at a staging area for transfer to the first workstation. The staging area can be thought as the place where the parts enter the system prior to going to the first workstation. No processing takes place at the staging area, other than preparation to be directed to the appropriate stations. After the parts have completed processing at the first workstation, they are transferred to a paint station manned by a second worker, and then to a packaging station where they are packed by a third worker, and then to a second staging area where they exit the system.
The time between part arrivals at the system is exponentially distributed with a mean of 28 minutes (stream 1). The processing time at the first workstation is uniformly distributed between 21 and 25 minutes (stream 2). The paint time is log-normally distributed with a mean of 22 minutes and a standard deviation of 4 (stream 3). The packing time follows a triangular distribution with a minimum of 20, mode of 22, and a maximum of 26 (stream 4). The transfers are unconstrained, in that they do not require a vehicle or resource, but all transfer times are exponential with a mean of 2 or 3 minutes (stream 5). Transfer times from the staging to the workstation and from pack to exit are 3 minutes. Transfer times from the workstation to paint and from paint to pack are 2 minutes. The performance measures of interest are the utilization and Work-In-Progress (WIP) at the workstation, paint and packaging operations. Figure 7.12 provides an illustration of the system.
(This problem is based on an example on page 209 and continues on page 217 of (Pegden et al. 1995). Used with permission)
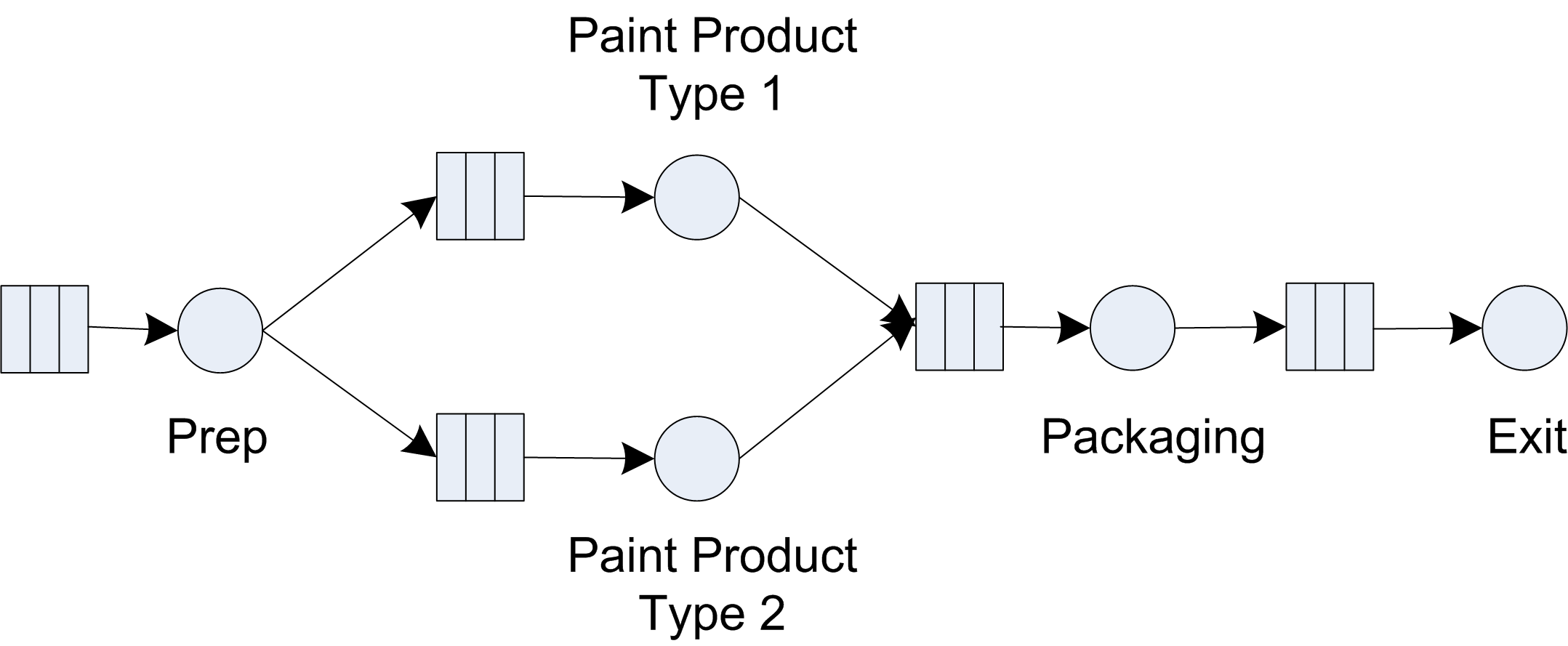
Figure 7.12: Simple painting flow line
Suppose that statistics on the part flow time, i.e. the total time a part spends in the system need to be collected. However, before simulating this process, it is discovered that a new part needs to be considered. This part will be painted a different color. Because the new part replaces a portion of the sales of the first part, the arrival process remains the same, but 30 percent of the arriving parts are randomly designated as the new type of part (stream 10). The remaining parts (70% of the total) are produced in the same manner as described above. However, the new part requires the addition of a different station with a painting time that is log-normally distributed with a mean of 49 minutes and a standard deviation of 7 minutes (stream 6). Assume that an additional worker is available at the new station. The existing station paints only the old type of part and the new station paints only the new parts. After the painting operation, the new part is transferred to the existing packing station and requires a packing time that follows a triangular distribution with a minimum value of 21, a mode of 23, and a maximum of 26 (stream 7). Run the model for 600,000 minutes with a 50,000 minute warm up period. If you were to select a resource to add capacity, which would it be?
Exercise 7.12 Suppose a service facility consists of two stations in series (tandem), each with its own FIFO queue. Each station consists of a queue and a single server. A customer completing service at station 1 proceeds to station 2, while a customer completing service at station 2 leaves the facility. Assume that the inter-arrival times of customers to station 1 are IID exponential random variables with a mean of 1.25 minutes (stream 1). Service times of customers at station 1 are exponential random variables with a mean of 0.7 minute (stream 2), and at station 2 are exponential random variables with mean 0.9 minute (stream 3).
Suppose that there is limited space at the second station. In particular, there is room for 1 customer to be in service at the second station and room for only 1 customer to wait at the second station. A customer completing service at the first station will not leave the service area at the first station unless there is a space available for it to wait at the second station. In other words, the customer will not release the server at the first station unless it can move to the second station.
Develop a model for this system. Run the simulation for exactly 20000 minutes with a warm up period of 2000 minutes for 20 replications and estimate for each station the expected average delay in queue for the customer, the expected time-average number of customers in queue, and the expected utilization. In addition, estimate the average number of customers in the system and the average time spent in the system. Is the buffer size between the stations sufficient for this situation?
Exercise 7.13 A particular stock keeping unit (SKU) has demand that averages 14 units per year and is Poisson distributed. That is, the time between demands is exponentially distributed with a mean a 1/14 years (stream 1). Assume that 1 year = 360 days. The inventory is managed according to a \((r, Q)\) inventory control policy with \(r = 3\) and \(Q = 4\). The SKU costs $150. An inventory carrying charge of 0.20 is used and the annual holding cost for each unit has been set at 0.2 * $150 = $30 per unit per year. The SKU is purchased from an outside supplier and it is estimated that the cost of time and materials required to place a purchase order is about $15. It takes 45 days to receive a replenishment order. The cost of back-ordering is very difficult to estimate, but a guess has been made that the annualized cost of a back-order is about $25 per unit per year.
Using simulate the performance of this system using \(Q = 4\) and \(r =3\). Report the average inventory on hand, the cost for operating the policy, the average number of back-orders, and the probability of a stock out for your model.
Now suppose that the lead-time is stochastic and governed by a lognormal distribution with a mean of 45 days and a standard deviation of 7 days (stream 2). What assumptions do you have to make to simulate this situation? Simulate this situation and compare/contrast the results with part (a).
Exercise 7.14 The Super Ready Auto Club has been serving customers for many years. The Super Ready Auto Club provides club, travel, and financial services to its members. One of its most popular services includes auto touring and emergency road service. Travel provides cruise packages, airline travel, and other vacation packages with special discounts for members. Finally, the financial services issues credit cards for members at special interest rates.
Super Ready Auto Club has regional call centers that handle incoming calls from members within a given region of the country. Table 7.9 presents the mean of the number of calls, recorded on an hourly basis over a period of 7 days, aggregated over a three state region.
The three types of service calls occur with 60% for auto service, 35% for credit card services, and 15% for travel services during the 8 am to 8 pm time frame. For the other hours of the day, the proportion changes to 90% for auto service, 10% for credit card services, and 0% for travel services. A sample of call service times were recorded for each of the types as shown in Tables 7.9, 7.10, (7.11, and (7.11. You can find this data in the chapter files that accompany this chapter in the spreadsheet called Super Ready Auto Club.xlsx. Use stream 1 for road side service calls, stream 2 for vacation service calls, and stream 3 for credit card service calls.
Call center operators cost $18 per hour including fringe benefits. It is important that the probability of a call waiting more than 3 minutes for an operator be less than 10%. Find a minimum cost staffing plan for each hour of the day for each day of the week that on-average meets the call probability waiting criteria. Measure the waiting time for a call, the average number of calls waiting, and the utilization of the operators. In addition, measure the waiting time of the calls by type.
What happens to the waiting times if road-side assistance calls are given priority over the credit card and travel service calls?
Consider how you would handle the following work rules. The operators should get a 10 minute break every 2 hours and a 30 minute food/beverage break every 4 hours. Discuss how you would staff the center under these conditions ensuring that there is always someone present (i.e. they are not all on break at the same time).
| Hour | Mon | Tue | Wed | Thur | Fri | Sat | Sun |
|---|---|---|---|---|---|---|---|
| 1 | 6.7 | 6.1 | 8.7 | 8.9 | 5.6 | 6.2 | 9.4 |
| 2 | 9.7 | 9.4 | 9.3 | 7.1 | 1.4 | 7.0 | 8.8 |
| 3 | 8.5 | 6.0 | 70.4 | 8.6 | 7.9 | 7.8 | 13.4 |
| 4 | 9.0 | 10.0 | 6.8 | 8.3 | 6.4 | 6.3 | 6.7 |
| 5 | 6.8 | 9.2 | 10.9 | 44.9 | 8.2 | 6.5 | 7.5 |
| 6 | 8.5 | 4.2 | 1.4 | 6.3 | 7.5 | 7.8 | 8.0 |
| 7 | 6.7 | 6.9 | 9.0 | 8.9 | 6.7 | 46.2 | 9.8 |
| 8 | 38.2 | 35.0 | 75.8 | 57.8 | 37.2 | 82.5 | 78.8 |
| 9 | 20.0 | 77.6 | 48.7 | 25.9 | 67.1 | 28.1 | 99.2 |
| 10 | 76.2 | 75.4 | 71.1 | 51.3 | 86.2 | 106.9 | 42.0 |
| 11 | 92.5 | 105.4 | 28.2 | 100.2 | 90.9 | 92.4 | 43.6 |
| 12 | 76.4 | 37.3 | 37.3 | 77.8 | 60.3 | 37.9 | 68.9 |
| 13 | 79.1 | 64.2 | 25.4 | 76.8 | 65.1 | 77.9 | 116.6 |
| 14 | 75.2 | 102.2 | 64.1 | 48.7 | 93.3 | 64.5 | 39.5 |
| 15 | 117.9 | 26.8 | 43.8 | 80.1 | 86.4 | 96.8 | 52.1 |
| 16 | 100.2 | 85.9 | 54.3 | 144.7 | 70.9 | 167.9 | 153.5 |
| 17 | 52.7 | 64.7 | 94.7 | 94.6 | 152.2 | 98.0 | 63.7 |
| 18 | 65.3 | 114.9 | 124.9 | 213.9 | 91.5 | 135.7 | 79.8 |
| 19 | 126.1 | 69.6 | 89.4 | 43.7 | 62.7 | 111.9 | 180.5 |
| 20 | 116.6 | 70.2 | 116.8 | 99.6 | 113.0 | 84.3 | 64.1 |
| 21 | 38.6 | 20.5 | 7.6 | 3.8 | 58.6 | 50.8 | 68.5 |
| 22 | 8.5 | 17.1 | 8.8 | 13.5 | 8.2 | 68.1 | 7.8 |
| 23 | 9.8 | 48.9 | 8.9 | 95.4 | 40.8 | 58.5 | 44.1 |
| 24 | 9.6 | 1.3 | 28.5 | 9.6 | 32.2 | 74.5 | 46.7 |
| 33.6 | 34.0 | 33.2 | 31.3 | 32.3 | 32.1 | 39.0 | 35.2 | 37.6 | 37.4 |
| 32.3 | 37.2 | 39.3 | 32.1 | 34.7 | 35.1 | 33.6 | 32.8 | 32.8 | 40.0 |
| 37.8 | 38.0 | 42.4 | 37.4 | 36.6 | 36.6 | 33.3 | 34.7 | 30.2 | 33.1 |
| 36.8 | 34.4 | 36.4 | 35.9 | 32.6 | 37.6 | 36.7 | 32.3 | 40.0 | 37.0 |
| 36.0 | 34.6 | 33.9 | 31.7 | 33.8 | 39.3 | 37.8 | 33.7 | 35.2 | 38.2 |
| 34.6 | 33.5 | 36.3 | 38.9 | 35.5 | 35.2 | 35.0 | 33.8 | 35.8 | 35.8 |
| 38.2 | 38.8 | 35.7 | 38.7 | 30.0 | 33.6 | 33.4 | 34.7 | 35.1 | 35.5 |
| 34.0 | 33.2 | 33.7 | 32.5 | 28.9 | 34.4 | 34.2 | 31.4 | 38.7 | 35.3 |
| 35.5 | 39.4 | 32.6 | 36.2 | 33.2 | 39.3 | 41.1 | 34.3 | 38.6 | 33.0 |
| 35.3 | 38.1 | 33.5 | 34.0 | 36.4 | 33.6 | 43.1 | 37.2 | 35.6 | 36.0 |
| 52.2 | 23.7 | 33.9 | 30.5 | 18.2 | 45.2 | 38.4 | 49.8 | 53.9 | 38.8 |
| 33.4 | 44.2 | 28.4 | 49.0 | 24.9 | 46.4 | 35.8 | 40.3 | 16.3 | 41.4 |
| 63.1 | 37.5 | 33.5 | 48.0 | 27.6 | 38.2 | 28.6 | 35.2 | 24.5 | 42.9 |
| 38.9 | 19.8 | 32.7 | 41.4 | 42.7 | 27.4 | 38.7 | 30.1 | 39.6 | 53.5 |
| 28.8 | 42.2 | 42.4 | 29.2 | 22.7 | 50.9 | 34.2 | 53.1 | 18.5 | 26.5 |
| 40.9 | 20.7 | 36.6 | 33.7 | 26.4 | 32.8 | 25.1 | 39.7 | 30.9 | 34.2 |
| 35.5 | 31.8 | 27.2 | 28.6 | 26.9 | 30.6 | 26.1 | 23.2 | 33.3 | 35.0 |
| 29.6 | 31.6 | 29.9 | 28.5 | 29.3 | 30.6 | 31.2 | 26.7 | 25.7 | 41.2 |
| 27.5 | 52.0 | 27.3 | 69.0 | 34.2 | 31.4 | 21.9 | 29.8 | 31.4 | 46.1 |
| 23.8 | 35.9 | 41.5 | 51.0 | 17.9 | 33.9 | 32.2 | 26.5 | 25.0 | 54.6 |
| 13.5 | 10.1 | 14.4 | 13.9 | 14.2 | 11.4 | 11.0 | 14.4 | 12.0 | 14.4 |
| 14.4 | 13.5 | 13.4 | 14.5 | 14.8 | 14.9 | 13.2 | 11.0 | 14.9 | 15.0 |
| 14.7 | 14.3 | 12.3 | 14.8 | 12.4 | 14.9 | 15.0 | 14.0 | 14.6 | 14.6 |
| 15.0 | 10.3 | 11.3 | 15.0 | 15.0 | 15.0 | 14.9 | 14.8 | 11.5 | 11.9 |
| 13.5 | 14.9 | 11.0 | 10.8 | 15.0 | 13.8 | 13.8 | 14.5 | 14.3 | 14.0 |
| 14.9 | 10.9 | 13.9 | 13.5 | 15.0 | 14.4 | 13.2 | 15.0 | 14.5 | 14.4 |
| 15.0 | 14.5 | 14.5 | 14.9 | 11.6 | 13.6 | 12.4 | 11.9 | 11.6 | 15.0 |
| 11.1 | 13.7 | 13.9 | 14.6 | 11.5 | 14.4 | 15.0 | 10.7 | 10.4 | 14.5 |
| 12.3 | 13.8 | 14.7 | 13.8 | 14.7 | 14.8 | 14.9 | 14.2 | 12.9 | 14.3 |
| 14.5 | 11.5 | 12.1 | 14.3 | 13.6 | 14.1 | 12.6 | 11.7 | 14.7 | 13.4 |
Exercise 7.15 Reconsider the STEM Career Fair Mixer Example. The results indicated that the utilization of the JHBunt recruiters was still high, around 90%, and the MalWart recruiters was low, around 50% after making the resource schedule changes. Design a schedule that gets both recruiting stations to about 80% during the peak period.
Exercise 7.16 Suppose a service facility consists of two stations in series (tandem), each with its own FIFO queue. Each station consists of a queue and a single server. A customer completing service at station 1 proceeds to station 2, while a customer completing service at station 2 leaves the facility. Assume that the inter-arrival times of customers to station 1 are IID exponential random variables with a mean of 1 minute (stream 1). Service times of customers at station 1 are exponential random variables with a mean of 0.7 minute (stream 2), and at station 2 are exponential random variables with mean 0.9 minute (stream 3). Assume that the travel time between the two stations must be modeled. The travel time is distributed according to a triangular distribution with parameters (1, 2, 4) minutes (stream 4).
Model the system assuming that the worker from the first station moves the parts to the second station. The movement of the part should be given priority if there is another part waiting to be processed at the first station.
Model the system with a new worker (resource) to move the parts between the stations.
From your models, estimate the total system time for the parts, the utilization of the workers, and the average number of parts waiting for the workers. Run the simulation for exactly 20000 minutes with a warm up period of 5000 minutes.
Exercise 7.17 Reconsider part (b) of Exercise 7.16. Instead of immediately moving the part, the transport worker waits until a batch of 5 parts has been produced at the first station. When this occurs, the worker moves the batch of parts to the second station. The parts are still processed individually at the second station. From your model, estimate the total system time for the parts, the utilization of the workers, and the average number of parts waiting for the workers. Run the simulation for exactly 20000 minutes with a warm up period of 5000 minutes.
Exercise 7.18 Redo Exercise 7.1 using resource constrained transfer. Assume that there are 2 workers at the diagnostic station, 1 worker per testing station, and 3 workers at the repair station. Thus, there are a total of 8 workers in the system. Furthermore, assume that any of these 8 workers are capable of moving parts between the stations. For example, when a part completes its operation at the diagnostic station, any worker in the system can carry the part to the next station. When a part requires movement, it will wait for the next available idle worker to complete the movement. Assume that parts waiting for processing at a station will be given priority over parts that require movement between stations. Build a simulation model that can assist the company in assessing the risks associated with the new contract under this resource constrained situation.
Exercise 7.19 Redo Exercise 7.2 assuming that there is a pool of 3 workers that perform the transport between the stations. Assume that the transport time is triangularly distributed with parameters (2, 4, 6) all in minutes (stream 13). Make an assessment for the company for the appropriate number of workers to have in the transport worker pool.
Exercise 7.20 Redo Exercise 7.10 assuming that there is a pool of 3 workers that perform the transport between the stations. Assume that the transport time is triangularly distributed with parameters (2, 4, 6) all in minutes. Make an assessment for the company for the appropriate number of workers to have in the transport worker pool.