7.2 Modeling Non-Stationary Systems

This section tackles a number of miscellaneous topics that can enhance your modeling capabilities. The section first examines the modeling of non-stationary arrival processes. This will motivate the exploration of additional concepts in resource modeling, including how to incorporate time varying resource staffing schedules. This will enable you to better model and tabulate the effects of realistic staff changes within systems. Because non-stationary arrivals affect how statistics should be interpreted, we will also study how to collect statistics over specific periods of time.

The section also covers some useful modeling situation involving how entities interact. The first situation that we will see is that of reneging from a queue. This will introduce how to remove entities that are in a queue and terminate their processes. Let’s get started by looking at how time dependent arrivals can be generated.

7.2.1 Non-Stationary Arrival Processes

If a process does not depend on time, it is said to be stationary. When a process depends on time, it is said to be non-stationary. The more formal definitions of stationary/non-stationary are avoided in the discussion that follows.

There are many ways in which you can model non-stationary (time varying) processes in your simulation models. Many of these ways depend entirely on the system being studied and through that study appropriate modeling methods will become apparent. For example, suppose that workers performing a task learn how to more efficiently perform the task every time that they repeat the task. The task time will depend on the time (number of previously performed tasks). For this situation, you might use a learning curve model as a basis for changing the task times as the number of repetitions of the task increases.

As another example, suppose the worker’s availability depends on a schedule, such as having a 30-minute break after accumulating so much time. In this situation, the system’s resources are dependent on time. Modeling this situation is described later in this section.

Let’s suppose that the following situation needs to be modeled. Workers are assigned a shift of 8 hours and have a quota to fill. Do you think that it is possible that their service times would, on average, be less during the latter part of the shift? Sure. They might work faster in order to meet their quota during the latter part of the shift. If you did not suspect this phenomenon and performed a time study on the workers in the morning and fit a distribution to these data, you would be developing a distribution for the service times during the morning. If you applied this distribution to the entire shift, then you may have a problem matching your simulation throughput numbers to the real throughput.

As you can see, if you suspect that a non-stationary process is involved, then it is critical that you also record the time that the observation was made. The time series plot that was discussed for input modeling helps in assessing non-stationary behavior; however, it only plots the order in which the data were collected. If you collect 25 observations of the service time every morning, you might not observe non-stationary behavior. To observe non-stationary behavior it is important to collect observations across periods of time.

One way to better plan your observations is to randomize when you will take the observations. Work sampling methods often require this. The day is divided into intervals of time and the intervals randomly selected in which to record an activity. By comparing the behavior of the data across the intervals, you can begin to assess whether time matters in the modeling as demonstrated in Section B.3.1. Even if you do not divide time into logical intervals, it is good practice to record the date and time for each of the observations that you make so that the observations can later be placed into logical intervals. As you may now be thinking, modeling a non-stationary process will take a lot of care and more observations than a stationary process.

A very common non-stationary process that you have probably experienced is a non- stationary arrival process. In a non-stationary arrival process, the arrival process to the system will vary by time (e.g., by hour of the day). Because the arrival process is a key input to the system, the system will thus become non-stationary. For example, in the drive-through pharmacy example, the arrival of customers occurred according to a Poisson process with mean rate \(\lambda\) per hour.

As a reminder, \(\lambda\) represents the mean arrival rate or the expected number of customers per unit time. Suppose that the expected arrival rate is five per hour. This does not mean that the pharmacy will get five customers every hour, but rather that on average five customers will arrive every hour. Some hours will get more than five customers and other hours will get less. The implication for the pharmacy is that they should expect about five per hour (every hour of the day) regardless of the time of day. Is this realistic? It could be, but it is more likely that the mean number of arriving customers will vary by time of day. For example, would you expect to get five customers per hour from 4 a.m. to 5 a.m., from 12 noon to 1 p.m., from 4 p.m. to 6 p.m.? Probably not! A system like the pharmacy will have peaks and valleys associated with the arrival of customers. Thus, the mean arrival rate of the customers may vary with the time of day. That is, \(\lambda\) is really a function of time, \(\lambda(t)\).

To more realistically model the arrival process to the pharmacy, you need to model a non-stationary arrival process. Let’s think about how data might be collected in order to model a non-stationary arrival process. First, as in the previous service time example, you need to think about dividing the day into logical periods of time. A pilot study may help in assessing how to divide time, or you might simply pick a convenient time division such as hours. You know that event generation logic requires a distribution that represents the time between arrivals. Ideally, you should collect the time of every arrival, \(T_i\), throughout the day. Then, you can take the difference among consecutive arrivals, \(T_i - T_{i-1}\) and fit a distribution to the inter-arrival times. Looking at the \(T_i\) over time may help to assess whether you need different distributions for different time periods during the day. Suppose that you do collect the observations and find that three different distributions are reasonable models given the following data:

Exponential, \(E[X] = 60\), for midnight to 8 a.m.
Lognormal, \(E[X] = 12\), \(Var[X] = 4\), for 8 a.m. to 4 p.m.
Triangular, min = 10; mode = 16; max = 20, for 4 p.m. to midnight

One simple method for implementing this situation is to switch to the appropriate distribution for the current time. In other words, schedule an event at midnight so that the time between arrival distribution can be set to exponential, schedule an event at 8 a.m. to switch to lognormal, and schedule an event at 4 p.m. to switch to triangular. This can easily be accomplished by holding the distributions within a list and using variable to determine which period of time is active and indexing into the list accordingly. Clearly, this varies the arrival process in a time-varying manner. There is nothing wrong with this modeling approach if it works well for the situation. In taking such an approach, you need a lot of data. Not only do you need to record the time of every arrival, but you need enough arrivals in order to adequately fit distributions to the time between events for various time periods. This may or may not be feasible in practice.

Often in modeling arrival processes, you cannot readily collect the actual times of the arrivals. If you can, you should try, but sometimes you just cannot. Instead, you are limited to a count of the number of arrivals in intervals of time. For example, a computer system records the number of people arriving every hour but not their individual arrival times. This is not uncommon since it is much easier to store summary counts than it is to store all individual arrival times. Suppose that you had count data as shown in Table 7.3.

Table 7.3: Example arrival counts
Interval	Mon	Tue	Wed	Thurs	Fri	Sat	Sun
12 am – 6 am	3	2	1	2	4	2	1
6 am - 9 am	6	4	6	7	8	7	4
9 am - 12 pm	10	6	4	8	10	9	5
12 pm - 2 pm	24	25	22	19	26	27	20
2 pm - 5 pm	10	16	14	16	13	16	15
5 pm - 8 pm	30	36	26	35	33	32	18
8 pm - 12 am	14	12	8	13	12	15	10

Of course, how the data are grouped into intervals will affect how the data can be modeled. Grouping is part of the modeling process. Let’s accept these groups as appropriate for this situation. Looking at the intervals, you see that more arrivals tend to occur from 12 pm to 2 pm and from 5 pm to 8 pm. As discussed in Section B.3.1, we could test for this non-stationary behavior and check if the counts depend on the time of day. It is pretty clear that this is the case for this situation. Perhaps this corresponds to when people who visit the pharmacy can get off of work. Clearly, this is a non-stationary situation. What kinds of models can be used for this type of count data?

A simple and often reasonable approach to this situation is to check whether the number of arrivals in each interval occurs according to a Poisson distribution. If so, then you know that the time between arrivals in an interval is exponential. When you can divide time so that the number of events in the intervals is Poisson (with different mean rates), then you can use a non-stationary or non-homogeneous Poisson process as the arrival process.

Consider the first interval to be 12 am to 6 am; to check if the counts are Poisson in this interval, there are seven data points (one for every day of the week for the given period). This is not a lot of data to use to perform a chi-square goodness-of-fit test for the Poisson distribution. So, to do a better job at modeling the situation, many more days of data are needed. The next question is: Are all the days the same? It looks like Sunday may be a little different than the rest of the days. In particular, the counts on Sunday appear to be a little less on average than the other days of the week. In this situation, you should also check whether the day of the week matters to the counts. As we illustrated in Section B.3.1, one method of doing this is to perform a contingency table test.

Let’s assume for simplicity that there is not enough evidence to suggest that the days are different and that the count data in each interval is well modeled with a Poisson distribution. In this situation, you can proceed with using a non-stationary Poisson process. From the data you can calculate the average arrival rate for each interval and the rate per hour for each interval as shown in Table 7.4. In the table, 2.14 is the average of the counts across the days for the interval 12 am to 6 pm. In the rate per hour column, the interval rate has been converted to an hourly basis by dividing the rate for the interval by the number of hours in the interval. Figure 7.6 illustrates the time-varying behavior of the mean arrival rates over the course of a day.

Table 7.4: Mean arrival rates for each time interval
Interval	Avg.	Length (hrs)	Rate per hour
12 am – 6 am	2.14	6	0.36
6 am - 9 am	6.0	3	2.0
9 am - 12 pm	7.43	3	2.48
12 pm - 2 pm	23.29	2	11.645
2 pm - 5 pm	14.29	3	4.76
5 pm - 8 pm	30.0	3	10
8 pm - 12 am	12.0	4	3.0

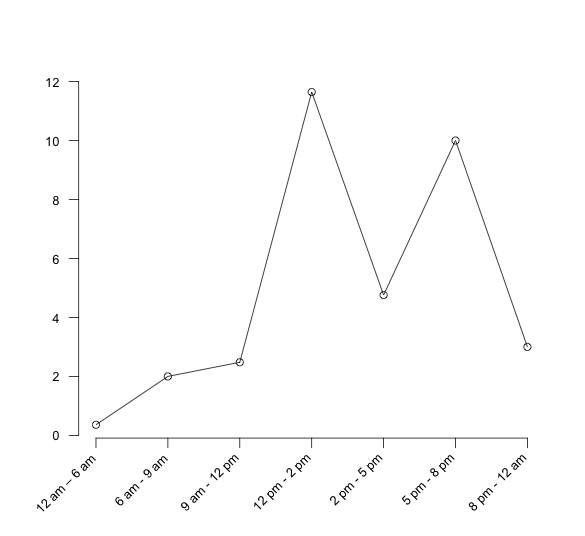
Figure 7.6: Arrival rate per hour for time intervals

The two major methods by which a non-stationary Poisson process can be generated are thinning and rate inversion. Both methods will be briefly discussed; however, the interested reader is referred to (L. M. Leemis and Park 2006) or (S. Ross 1997) for more of the theory underlying these methods. Before these methods are discussed, it is important to point out that the naive method of using different Poisson processes for each interval and subsequently different exponential distributions to represent the inter-arrival times could be used to model this situation by switching the distributions as previously discussed. However, the switching method is not technically correct for generating a non-stationary Poisson process. This is because it will not generate a non-stationary Poisson process with the correct probabilistic underpinnings. Thus, if you are going to model a process with a non-stationary Poisson process, you should use either thinning or rate inversion to be technically correct.

7.2.1.1 Thinning Method

For the thinning method, a stationary Poisson process with a constant rate,\(\lambda^{*}\), and arrival times, \(t_{i}^{*}\), is first generated, and then potential arrivals, \(t_{i}^{*}\), are rejected with probability:

\[p_r = 1 - \frac{\lambda(t_{i}^{*})}{\lambda^{*}}\]

where \(\lambda(t)\) is the mean arrival rate as a function of time. Often, \(\lambda^{*}\) is set as the maximum arrival rate over the time horizon, such as:

\[\lambda^{*} = \max\limits_{t} \lbrace \lambda(t) \rbrace\]

In the example, \(\lambda^{*}\) would be the mean of the 5 pm to 8 pm interval, \(\lambda^{*} = 11.645\).

Example 7.5 (Thinning Algorithm Implementation) The following code for implementing the thinning method creates event times at the maximum rate and thins them according to the current time.

fun nhppThinning(rateFunc: RateFunctionIfc, maxTime: Double) : DoubleArray {
    val list = mutableListOf<Double>()
    val rv = ExponentialRV(1.0/rateFunc.maximumRate)
    val u = UniformRV(0.0, rateFunc.maximumRate)
    var t = 0.0
    while (t < maxTime){
        var s = t
        do{
            s = s + rv.value
        } while((s < maxTime) && (u.value > rateFunc.rate(s)))
        t = s
        if (t < maxTime){
            list.add(t)
        }
    }
    return list.toDoubleArray()
}

The function returns the time of the events. To be able to use such numbers in an event generator, we need to generate the time between random events for the non-homogeneous Poisson process. The KSL provides such a random variable via the NHPPTimeBtwEventRV class found in the ksl.modeling.nhpp package. The above code, which can be found in the examples for this chapter, uses an instance that implements the RateFunctionIfc interface. The ksl.modeling.nhpp package provides implementations for piecewise constant and piecewise linear rate functions. The following code illustrates how to create and simulate a piecewise constant rate function using the thinning method.

fun main() {
    val d = doubleArrayOf(15.0, 20.0, 15.0)
    val ar = doubleArrayOf(1.0, 2.0, 1.0)
    val f = PiecewiseConstantRateFunction(d, ar)
    println("-----")
    println("intervals")
    println(f)
    val times = nhppThinning(f, 50.0)
    println(times.contentToString())
}

This code simulates the following piecewise rate function:

\[ f(x) = \begin{cases} 1.0 & 0.0 \leq x \leq 15.0\\ 2.0 & 15.0 \leq x \leq 35.0\\ 1.0 & 35.0 \leq x \leq 50.0\\ \end{cases} \] Notice that the rate and the duration values are provided as arrays. The theoretical basis for why thinning works can be found in (S. Ross 1997).

7.2.1.2 Rate Inversion Method

The second method for generating a non-stationary Poisson process is through the rate inversion algorithm. In this method, a \(\lambda = 1\) Poisson process is generated, and the inverse of the mean arrival rate function is used to re-scale the times of arrival to the appropriate scale. Define \(m(t)\) as the cumulative mean rate function such that:

\[ m(t) = \int_0^t \lambda(s)ds \quad \text{if} \, \, t \leq 0 < \tau \] where \(\lambda(\cdot)\) is the instantaneous mean rate function defined over a range from 0 to \(\tau\). Define \(m^{-1}(t)\) as the inverse of \(m(t)\). Then, the following algorithm will generate a non-homogeneous Poisson process. Define \(a_0 = 0\), \(y_0 = 0.0\), and \(n = 0\).

while (\(a_n < \tau\)) {

\(y_{n+1} = y_n\) + ExponentialRV(mean=1.0)

\(a_{n+1} = m^{-1}(y_{n+1})\)

\(n = n + 1\)

}

The resulting array, \(a_i\) holds the generated event times. This algorithm is discussed further in (S. Ross 1997). The algorithm generates a rate 1.0 Poisson process and transforms the resulting event times to the times on the \(m^{-1}(t)\) axis. The resulting event times will be from a non-homogeneous Poisson process.

The KSL provides classes for piecewise constant and piecewise linear rate functions and their inverse cumulative rate functions.

Example 7.6 (Piecewise Constant Rate Function) The following example illustrates how to setup a piecewise linear rate function and generate from it using a NHPPEventGenerator instance.

class NHPPPWLinearExample(parent: ModelElement, f: PiecewiseRateFunction, name: String? = null) 
: ModelElement(parent, name) {

    private val myNHPPGenerator: NHPPEventGenerator = NHPPEventGenerator(this, f, this::arrivals, streamNum = 1)
    private val myCountersFC: MutableList<Counter> = mutableListOf()
    private val myPWRF: PiecewiseRateFunction = f

    init {
        val n: Int = f.numberSegments()
        for (i in 0 until n) {
            val c = Counter(this, "Interval FC $i")
            myCountersFC.add(c)
        }
    }

    private fun arrivals(generator: EventGenerator){
        val t: Double = time
        val i: Int = myPWRF.findTimeInterval(t)
        myCountersFC[i].increment()
    }
}

In the code, a list of counters is defined to collect the counts within the intervals of the function. The end points of the segments are the rates at the beginning and end of the segments. The rate at the beginning of the segment can be the same as the rate at the end of the segment. The example has two arrays, one for the rate values and one for the duration values. In the example, the first segment has beginning rate \(\lambda_0 = 0.5\), duration 200.0, and ending rate, \(\lambda_1 = 0.5\). The second segment begins with \(\lambda_1 = 0.5\), has duration 400.0, and ending rate \(\lambda_2 = 0.9\). Thus, there will be one more specified rate value than there will be duration values. To specify a piecewise linear rate function, you must have at least one segment.

fun main() {
    val ar = doubleArrayOf(0.5, 0.5, 0.9, 0.9, 1.2, 0.9, 0.5)
    val dd = doubleArrayOf(200.0, 400.0, 400.0, 200.0, 300.0, 500.0)

    val f = PiecewiseLinearRateFunction(dd, ar)
    // create the experiment to run the model
    val s = Model()
    println("-----")
    println("intervals")
    System.out.println(f)
    NHPPPWLinearExample(s, f)

    // set the parameters of the experiment
    s.numberOfReplications = 1000
    s.lengthOfReplication = 2000.0

    // tell the simulation to run
    s.simulate()
    val r = s.simulationReporter
    r.printAcrossReplicationSummaryStatistics()
}

The output is what would be expected for this process. The interested reader is referred to (L. M. Leemis and Park 2006) for why the slope of the segments play such an important role.

intervals
 [0.5,0.5] slope = 0.0 [0.0,200.0] width = 200.0 [0.0,100.0] cr width = 100.0
 [0.5,0.9] slope = 0.001 [200.0,600.0] width = 400.0 [100.0,380.0] cr width = 280.0
 [0.9,0.9] slope = 0.0 [600.0,1000.0] width = 400.0 [380.0,740.0] cr width = 360.0
 [0.9,1.2] slope = 0.0014999999999999996 [1000.0,1200.0] width = 200.0 [740.0,950.0] cr width = 210.0
 [1.2,0.9] slope = -9.999999999999998E-4 [1200.0,1500.0] width = 300.0 [950.0,1265.0] cr width = 315.0
 [0.9,0.5] slope = -8.0E-4 [1500.0,2000.0] width = 500.0 [1265.0,1615.0] cr width = 350.0

-------------------------------------------------------------------------------

Across Replication Statistical Summary Report
Sat Dec 31 18:03:58 CST 2022
Simulation Results for Model: MainModel


Number of Replications: 1000
Length of Warm up period: 0.0
Length of Replications: 2000.0

-------------------------------------------------------------------------------
Counters
-------------------------------------------------------------------------------
Name                                  Average       Std. Dev.    Count 
-------------------------------------------------------------------------------
Interval FC 0                       99.899000       10.144837     1000.000000 
Interval FC 1                      279.526000       16.741673     1000.000000 
Interval FC 2                      359.733000       18.398538     1000.000000 
Interval FC 3                      209.719000       14.505532     1000.000000 
Interval FC 4                      315.231000       17.753502     1000.000000 
Interval FC 5                      349.919000       18.208899     1000.000000 
-------------------------------------------------------------------------------

The advantage of the rate inversion method is that there is a one for one mapping from the underlying pseudo-random numbers and the generated variates. Since the thinning method uses a form of acceptance-rejection, the one-for-one mapping can not be preserved. The disadvantage of the rate inversion method is that the mean cumulative rate function, \(m(t)\) must be inverted, which may require numerical methods. The following section discusses the issues involved when using resources under non-stationary conditions.

7.2.2 Modeling Resources Under Non-Stationary Conditions

From previous modeling, a resource can be something that an entity uses as it flows through the system. If the required units of the resource are available for the entity, then the units are allocated to the entity. If the required units are unavailable for allocation, the entity’s progress through the model stops until the required units become available. So far, the only way in which the units could become unavailable was for the units to be seized by an entity. The seizing of at least one unit of a resource causes the resource to be considered busy. A resource is considered to be in the idle state when all units are idle (no units are seized). Thus, in previous modeling a resource could be in one of two states: Busy or Idle.

When specifying a resource, its capacity must be given. The capacity represents the maximum number of units of the resource that can be seized at any time. In previous modeling, the capacity of the resource was fixed. That is, the capacity did not vary as a function of time. When the capacity of a resource was set, the resource had that same capacity for all of the replications; however, in many situations, the capacity of a resource can vary with time. For example, in the pharmacy model, you might want to have two or more pharmacists staffing the pharmacy during peak business hours. This type of capacity change is predictable and can be managed via a staffing schedule. Alternatively, the changes in capacity of a resource might be unpredictable or random. For example, a machine being used to produce products on a manufacturing line may experience random failures that require repair. During the repair time, the machine is not available for production. The KSL provides constructs for modeling scheduled capacity changes.

Currently, the KSL permits resources that use a singular request queue to experience capacity changes. That is, the ResourceWithQ implementation can handle capacity changes; however, the Resource class implementation does not permit the capacity to change. If you need a resource that experiences capacity changes, then you need to declare it as a ResourceWithQ instance. This limitation occurs because capacity increases require the newly available units to be allocated to any waiting requests. In general, an instance of a Resource can be involved with more than one request queue due to arbitrary combinations of seize() calls involving the resource. That is, the requests for an instance of Resource may in fact wait in different queues due to the flexible modeling provided by the implementations of the seize() method. Currently, the possible multiple instances of RequestQ that could be involved with a Resource is not tracked. Even if the tracking occurred, then issues would still remain about how to allocate the new capacity across requests that are waiting in different instances of RequestQ. Future work may consider solutions to these issues; however, the current implementation of capacity schedules simplifies this situation by only permitting capacity changes for instances of the ResourceWithQ class. Finally, the modeling of resources that can fail is under consideration for future development.

There are two key resource variables for understanding resources and their states.

\(c(t)\): Resource capacity, \(c(t)\), returns the number of capacity units currently defined for the specified resource. This value can be changed by the user via a capacity schedule or through the use capacity change notices.
\(b(t)\): Number of busy resource units at any time \(t\). Each time an entity seizes a resource, \(b(t)\) changes accordingly.
\(a(t) = c(t) - b(t)\): Number of available resource units at any time \(t\). Each time an entity seizes a resource or a capacity change occurs, \(a(t)\) changes accordingly.

These variables may change over time for a resource. The changing of these variables defines the possible states of a resource. These states are:

Idle: A resource is in the idle state when all units are idle. That is, a resource is idle if there are no busy units, i.e. \(b(t) = 0\).
Busy: A resource is in the busy state when it has one or more busy (seized) units. That is, when \(b(t) > 0\).
Inactive: A resource is in the inactive state when it has zero capacity and it is not busy. That is, when \(b(t) = 0\) and \(c(t) = 0\). Because of how capacity changes can be invoked, it is possible for the capacity of the resource to be \(c(t) = 0\) while resources are still busy. This will be discussed further in what follows.

A capacity schedule governs how capacity changes. The CapacitySchedule class specifies the amount of capacity for various durations of time. For example, in the following code, we specify a resource with a default initial capacity of 2 units, which is overridden by specifying the use of a capacity schedule.

    private val resource: ResourceWithQ = ResourceWithQ(this, name = "Resource", capacity = 1)
    private val schedule: CapacitySchedule

    init {
        schedule= CapacitySchedule(this, 0.0)
        schedule.addItem(capacity = 0, duration = 15.0)
        schedule.addItem(capacity = 1, duration = 35.0)
        schedule.addItem(capacity = 0, duration = 20.0)
        schedule.addItem(capacity = 2, duration = 30.0)
        resource.useSchedule(schedule, changeRule = CapacityChangeRule.IGNORE)
    }

A capacity schedule provides a start time for the schedule. That is, the time after the start of the replication for which the schedule starts and the items on the schedule get processed. In the example, the starting time of the schedule is specified in the constructor of CapacitySchedule as 0.0. Then, the addItem method is used to add capacity values and duration values (pairs). In the example, notice that the capacity can be 0 for different segments of time and that a capacity change rule is specified when indicating that the resource uses the schedule.

If the capacity is increased over its current value and there are no pending changes, then the capacity is immediately increased and requests that are waiting for the resource will be processed to receive allocations from the resource. If the capacity is decreased from its current value, then the amount of the decrease is first filled from idle units. If there are not enough idle units to complete the decrease, then the change is processed according to the capacity change rule. The following discusses the two capacity change rule options available within the KSL.

Ignore: starts the time duration of the schedule change immediately, but allows the busy resource to finish processing the current entity before causing the capacity change.
Wait: waits until the busy resource has finished processing the current entity before changing the resource capacity and starting the time duration of the schedule change.

It is important to note that the capacity change rule is invoked only when the resource is busy and there is a requested decrease in capacity. The rules govern when the change occurs. Basically, the ignore rule indicates that the change starts immediately. That is, the resource acts as if the capacity has been removed by putting up a sign indicating that the change has immediately reduced the capacity. The variable, \(a(t)\), may in fact become less than zero in this case. That is, the ignore rule may cause a deficit in capacity. Since the resource is also busy, there will not be any available units and any new seize requests will wait and any currently waiting requests will continue to wait. The requested units will be taken away and not be allowed to be allocated as the required number is released from the resource. Let’s consider some cases of this situation.

Let’s suppose that your simulation professor has office hours throughout the day, except from 12-12:30 pm for lunch. What happens for each rule if you arrive at 11:55 am with a question?

Ignore Case 1:

You arrive at 11:55 am with a 10 minute question and begin service.
At Noon, the professor gets up and hangs a Lunch in Progress sign.
Your professor continues to answer your question for the remaining service time of 5 minutes.
You leave at 12:05 pm.
Whether or not there are any students waiting in the hallway, the professor still starts lunch.
At 12:30 pm the professor finishes lunch and takes down the lunch in progress sign. If there were any students waiting in the hallway, they can begin service.

The net effect of case 1 is that the professor lost 5 minutes of lunch time. During the 30 minute scheduled break, the professor was busy for 5 minutes and inactive for 25 minutes.

Ignore Case 2:

You arrive at 11:55 am with a 45 minute question and begin service.
At Noon, the professor gets up and hangs a Lunch in Progress sign.
Your professor continues to answer your question for the remaining service time of 40 minutes.
At 12:30 pm the professor gets up and takes down the lunch in progress sign and continues to answer your question.
You leave at 12:40 pm

The net effect of case 2 is that the professor did not get to eat lunch that day. During the 30 minute scheduled break, the professor was busy for 30 minutes.

This rule is called Ignore since the scheduled break may be ignored by the resource if the resource is busy when the break occurs. Technically, the scheduled break actually occurs and the time that was scheduled may be considered as unscheduled (inactive) time.

Let’s assume that the professor is at work for 8 hours each day (including the lunch break). But because of the scheduled lunch break, the total time available for useful work is 450 minutes. In case 1, the professor worked for 5 minutes more than they were scheduled. In case 2, the professor worked for 30 minutes more than they were scheduled. As will be indicated shortly, this extra work time, must be factored into how the utilization of the resource (professor) is computed.

The situation is a bit more complex because another scheduled change may be required to occur (either positive or negative) while a current scheduled change is in progress. For the ignore case, if a positive change occurs before the end of the currently scheduled change, its duration must be long enough for the change to last longer than the current change’s end time. That is, the next change cannot be scheduled to end before the current change ends. If we have a legal change notice, then if the change is a positive change, it happens immediately. In essence the current negative change is cancelled and the positive change occurs. If the change is a negative change, then its end is scheduled, but it waits until the current negative change completes before proceeded with the new negative change. Thus, for ignore, negative changes can pile up if they occur sequentially.

Now, let’s examine what happens if the rule is Wait.

Wait Case 1:

You arrive at 11:55 am with a 10 minute question and begin service.
At Noon, the professor’s lunch reminder rings on his or her computer. The professor recognizes the reminder but doesn’t act on it, yet.
Your professor continues to answer your question for the remaining service time of 5 minutes.
You leave at 12:05 pm. The professor recalls the lunch reminder and hangs a Lunch in Progress sign. Whether or not there are any students waiting in the hallway, the professor still hangs the sign and starts a 30 minute lunch.
At 12:35 pm the professor finishes lunch and takes down the lunch in progress sign. If there were any students waiting in the hallway, they can begin service.

Wait Case 2:

You arrive at 11:55 am with a 45 minute question and begin service.
At Noon, the professor’s lunch reminder rings on his or her computer. The professor recognizes the reminder but doesn’t act on it, yet.
Your professor continues to answer your question for the remaining service time of 40 minutes.
You leave at 12:40 pm. The professor recalls the lunch reminder and hangs a Lunch in Progress sign. Whether or not there are any students waiting in the hallway, the professor still hangs the sign and starts a 30 minute lunch.
At 1:10 pm the professor finishes lunch and takes down the lunch in progress sign. If there were any students waiting in the hallway, they can begin service.

The net effect of both these cases is that the professor does not miss lunch (unless the student’s question takes the rest of the afternoon!). Thus, in this case the resource will experience the scheduled break after waiting to complete the entity in progress. Again, in this case, the tabulation of the amount of busy time may be affected by when the rule is invoked

The example involving the professor involved a resource with 1 unit of capacity. But what happens if the resource has a capacity of more than 1 and what happens if the capacity change is more than 1. The rules work essentially the same. If the scheduled change (decrease) is less than or equal to the current number of idle units, then the rules are not invoked. If the scheduled change will require busy units, then any idle units are first taken away and then the rules are invoked. In the case of the ignore rule, the units continue serving, the inactive sign goes up, and whichever unit is released first becomes inactive first.

In the case of the Ignore rule, a positive change happens immediately. In the case of the wait rule, the positive change will be delayed until after the full duration of the negative change. Thus, for the wait rule, the changes are shifted in time, but will always occur (provided that the simulations’ replication length is long enough). Thus, for the wait rule, once a capacity change is delayed because of being invoked when the resource is busy, all subsequent changes will also be delayed. In essence, the capacity changes are handled in a first-come, first served manner. Both rules ensure that an entity that is using the resource at the time of change will fully complete its current usage. Once the entity releases the resource, the rule governs how the resource’s released units are allocated to the change. In the case of a positive change, the units are given back to the resource at the time of the release. In the case of a negative change, the units are taken away from the current capacity, \(c(t)\). Since the rules affect the allocation of capacity, they can affect how the utilization of the resource is computed.

The calculation of instantaneous and scheduled utilization depends upon the two variables \(b(t)\) and \(c(t)\) for a resource. The instantaneous utilization is defined as the time weighted average of the ratio of these variables. Let \(b(t)\) be the number of busy resource units at time \(t\). Then, the time average number of busy resources is:

\[\overline{B} = \frac{1}{T}\int\limits_0^T \mathit{b}(t) \mathrm{d}t\]

Let \(c(t)\) be the capacity of the resource at time \(t\). Then, the time average capacity of the resource is:

\[\overline{C} = \frac{1}{T}\int\limits_0^T \mathit{c}(t) \mathrm{d}t\]

Now, we can define the instantaneous utilization at time \(t\) as:

\[IU(t) = \begin{cases} 0 & c(t) = 0\\ 1 & b(t) \geq c(t)\\ b(t)/c(t) & \text{otherwise} \end{cases}\]

Thus, the time average instantaneous utilization is:

\[\overline{\mathit{IU}} = \frac{1}{T}\int\limits_0^T \mathit{IU}(t)\mathrm{d}t\]

The scheduled utilization is the time average number of busy resources divided by the time average number scheduled. As can be seen in Equation (7.1), this is the same as the total time spent busy divided by the total time available for all resource units.

\[\begin{equation} \overline{\mathit{SU}} = \frac{\overline{B}}{\overline{C}} = \frac{\frac{1}{T}\int\limits_0^T b(t)dt}{\frac{1}{T}\int\limits_0^T c(t)dt} = \frac{\int\limits_0^T b(t)dt}{\int\limits_0^T c(t)dt} \tag{7.1} \end{equation}\]

If \(c(t)\) is constant, then \(\overline{\mathit{IU}} = \overline{\mathit{SU}}\). Caution should be used in interpreting \(\overline{\mathit{IU}}\) when \(c(t)\) varies with time.

Now let’s return to the example of the professor holding office hours. Let’s suppose that the ignore option is used and consider case 2 and the 45 minute question. Let’s also assume for simplicity that the professor had a take home exam due the next day and was therefore busy all day long. What would be the average instantaneous utilization and the scheduled utilization of the professor? Table 7.5 illustrates the calculations.

Table 7.5: Example Calculation for professor utilization
Time interval	Busy time	Scheduled time	\(b(t)\)	\(c(t)\)	\(\mathit{IU}(t)\)
8 am - noon	240	240	1.0	1.0	1.0
12 - 12:30 pm	30	0	1.0	0	1.0
12:30 - 4 pm	210	210	1.0	1.0	1.0
	480	450

From Table 7.5 we can compute \(\overline{B}\) and \(\overline{C}\) as:

\[\begin{aligned} \overline{B} & = \frac{1}{480}\int\limits_{0}^{480} 1.0 \mathrm{d}t = \frac{480}{480} = 1.0 \\ \overline{C} & = \frac{1}{480}\int\limits_{0}^{480} \mathit{c(t)} \mathrm{d}t = \frac{1}{480}\biggl\lbrace\int\limits_{0}^{240} 1.0 \mathrm{d}t + \int\limits_{270}^{480} 1.0 \mathrm{d}t \biggr\rbrace = 450/480 = 0.9375\\ \overline{\mathit{IU}} & = \frac{1}{480}\int\limits_{0}^{480} 1.0 \mathrm{d}t = \frac{480}{480} = 1.0\\ \overline{\mathit{SU}} & = \frac{\overline{\mathit{NR}}}{\overline{\mathit{MR}}} = \frac{1.0}{0.9375} = 1.0\bar{6}\end{aligned}\] Table 7.5 indicates that \(\overline{IU}\) = 1.0 (or 100%) and \(\overline{SU}\) = 1.06 (or 106%). Who says that professors don’t give their all! Thus, with scheduled utilization, a schedule can result in the resource having its scheduled utilization higher than 100%. There is nothing wrong with this result, and if it is the case that the resource is busy for more time than it is scheduled, you would definitely want to know.

The choice of which rule to use comes down to what is given priority. The Ignore rule gives priority to the entity by cutting short the scheduled change. The Wait rule gives priority to the resource by ensuring that the scheduled change always occurs. If the resources are people, then using the Wait rule seems more appropriate. Of course, if these rules do not meet the requirements of your modeling situation, you are always free to implement difference rules. In the next section, the arrival schedules and capacity schedules are used to enhance the STEM Career Mixer modeling.

7.2.3 Enhancing the STEM Career Mixer Model

In Chapter 6, we discussed the implementation of a model for the STEM Career Fair Mixer of Example 6.8. In this section, we put the non-stationary modeling concepts of the previous sections into practice by exploring an enhanced version of the STEM Career Fair Mixer system.

Example 7.7 (Non-Stationary STEM Career Fair Mixer) In this example, we embellish the STEM Career Fair mixer model to add a few modeling issues that will make the model a bit more realistic in order to illustrate the non-stationary modeling constructs provided by the KSL. The following issues will be addressed in the new model.

In reality, those students that wander around before deciding to visit the recruiters actually visit the conversation area associated with the mixer. The organizer of the event has asked alumni to volunteer to be available within the conversation area to chat with students and discuss their career development. After all, it is a mixer. The organizer of the mixer would like to plan for the size of the conversation area.
The STEM Fair is scheduled for 6 hours; however, currently, the simulation simply ends “abruptly” at 6 hours. How should we handle those students that are attending the mixer when the mixer ends? In this section, we will model a more realistic approach to ending the mixer and handling the students in progress.

After discussing with the STEM Fair organizer, the following additional facts were discovered. Generally, near the end of the scheduled mixer time, an announcement is made to everyone in the facility through the public address (PA) system that the mixer will be ending soon. For the purposes of this modeling enhancement, we can assume that the announcement goes out 15 minutes before the end of the mixer. At that time, we can assume the following:

The doors to the mixture are closed to new arrivals. In other words, a closed sign goes up so that no new students are admitted to the mixer.
Any students that were chatting within the conversation area finish up their conversations and then head for the exit, without visiting the recruiting stations.
Any student walking to the name tag area, the conversation area or to the recruiting area proceed to the exit.
Any students already at the recruiting stations, either in line waiting, or talking with the recruiter are allowed to finish up their visit and then depart the mixer.

Based on additional observations and discussion with the STEM mixer organizer, the following changes can be assumed:

Because the distances between the stations in the hall are now important an enhanced drawing of the system has been made that better illustrates the standard layout that has been used in the past for the mixer. The distances shown in the drawing are rough estimates.
New data suggest that 60% of the arriving students do not visit the conversation area, but instead go directly to the recruiting area to pick one of the two recruiting stations to visit, with equal probability.
The remaining 40% of students will first visit the conversation area. The time spent within the conversation area is a little less than previously noted to exclude the time spent walking. The conversation time is triangularly distribution with a minimum of 10 minutes, a most likely value of 15 minutes, and a maximum value of 30 minutes. After having their conversations, 90% of the students decide to visit one of the two recruiting stations. The other 10% are too tired or timid and decide to leave.
The speed of people walking can vary greatly, but prior data suggests that for short distances within and around buildings, people walk between 1 mile per hour and 3 miles per hour, with a most likely time of 2 miles per hour, triangularly distributed.

After further conversations with students who have attended past mixers, it was discovered that there really isn’t a preference for visiting one of the recruiters first. Instead, after arriving to the recruiting area, students decide to visit the recruiter that has the least number of people (waiting and interacting with the recruiters). If both recruiter locations have the same total number of students, then the students show no preference between the two recruiters. After visiting both, they depart.

Finally, suppose that new data on the arrival behavior of the students have become available. Over the course of the 6 hours that the mixer is open, the new data indicates that the rate varies significantly by the time of day. Let’s assume that the Mixer opens at 2 pm and lasts until 8 pm. Data was collected over 30 minute intervals during the 6 hours of the mixer and it showed that there was a larger arrival rate during the middle hours of the operating hours than during the beginning or ending hours of the data. The Table 7.6 summarizes the arrival rate for each 30 minute period throughout the 6 hour period.

Table 7.6: Student hourly arrival rates by 30 minute periods
Period	Time Frame	Duration	Mean Arrival Rate per Hour
1	2 - 2:30 pm	30	5
2	2:30 – 3 pm	30	10
3	3 - 3:30 pm	30	15
4	3:30 – 4 pm	30	25
5	4 - 4:30 pm	30	40
6	4:30 – 4 pm	30	50
7	5 - 5:30 pm	30	55
8	5:30 – 6 pm	30	60
9	6 - 6:30 pm	30	60
10	6:30 – 7 pm	30	30
11	7 - 7:30 pm	30	5
12	7:30 – 8 pm	30	5

Because of the time varying nature of the arrival of students, the STEM mixer organizers have noticed that during the peak period of the arrivals there are substantially longer lines of students waiting to speak to a recruiter and often there are not enough tables within the conversation area for students. Thus, the mixer organizers would like to advise the recruiters as to how to staff their recruiting stations during the event. As part of the analysis, they want to ensure that 90 percent of the students experience an average system time of 35 minutes or less during the 4:30-6:30 pm time frame. They would also like to measure the average number of students waiting for recruiters during this time frame as well as the average number of busy recruiters at the MalWart and JHBunt recruiting stations. You should first perform an analysis based on the current staffing recommendations from the previous modeling and then compare those results to a staffing plan that allows the recruiters to change their assigned number of recruiters by hour.

Because of these changes to the modeling assumptions, the STEM organizer would like to better understand the following aspects of potential system performance.

When the PA announcement occurs, how many students on average are:
- In the conversation area
- Attending the MalWart recruiting station
- Attending the JHBunt recruiting station
How long after the 6-hour scheduled time does the mixer actually end? That is, since all students are permitted to finish up what they are currently doing when the PA announcement occurs, how long does it take for the hall to be completely empty?
How many students, on average, are in the conversation area?

7.2.3.1 Modeling Walking Time

To model the walking within the mixer, we need to translate the distance travelled into time. Since we are told the typical velocity for walking within a building for a person, we can randomly generate the velocity associated with a walking trip. Then, if we know the distance to walk, we can determine the time via the following relationship, where \(v\) is the speed (velocity), \(d\) is the distance, and \(t\) is the time.

\[v = \frac{d}{t}\]

Thus, we can randomly generate the value of \(v\), and use the relationship to determine the time taken.

\[t = \frac{d}{v}\]

We know that the speed of people walking is triangularly distributed with a minimum of 1 mile per hour, a mode of 2 miles per hour, and a maximum of 3 miles per hour. This translates into a minimum of 88 feet per minute, a mode of 176 feet per minute, and a maximum of 264 feet per minute. Thus, we represent the speed as a random variable, Speed ~ TRIA(88, 176, 264) feet per minute and if we know the distance to travel, we can compute the time.

We have the following distances between the major locations of the system:

Entrance to Name Tags, 20 feet
Name Tags to Conversation Area, 30 feet
Name Tags to Recruiting Area (either JHBunt or MalMart), 80 feet
Name Tags to Exit, 140 feet
Conversation Area to Recruiting Area (either JHBunt or MalMart), 50 feet
Conversation Area to Exit, 110 feet
Recruiting Area (either JHBunt or MalMart) to Exit, 60 feet

For simplicity, we assume that the distance between the JHBunt and MalWart recruiting locations within the recruiting area can be ignored.

7.2.3.2 Collecting Statistics Over Periods of Time

For some modeling situations, we need to be able to collect statistics during specific intervals of time. To be able to do this, we need to be able to observe what happens during those intervals. In general, to collect statistics during a particular interval of time will require the scheduling of events to observe the system (and its statistics) at the start of the period and then again at the end of the period in order to record what happened during the period. Let’s define some variables to clarify the concepts. We will start with a discussion of collecting statistics for tally-based data.

Let \(\left( x_{1},\ x_{2},x_{3},\cdots{,x}_{n(t)} \right)\) be a sequence of observations up to and including time \(t\).

Let \(n(t)\) be the number of observations up to and including time \(t\).

Let \(s\left( t \right)\) be the cumulative sum of the observations up to and including time \(t\). That is,

\[s\left( t \right) = \sum_{i = 1}^{n(t)}x_{i}\]

Let \(\overline{x}\left( t \right)\) be the cumulative average of the observations up to and including time \(t\). That is,

\[\overline{x}\left( t \right) = \frac{1}{n(t)}\sum_{i = 1}^{n(t)}x_{i} = \frac{s\left( t \right)}{n(t)}\]

We should note that we have \(s\left( t \right) = \overline{x}\left( t \right) \times n(t)\). Let \(t_{b}\) be the time at the beginning of a period (interval) of interest and let \(t_{e}\) be the time at the end of a period (interval) of interest such that \(t_{b} \leq t_{e}\). Define \(s(t_{b},t_{e}\rbrack\) as the sum of the observations during the interval, \((t_{b},t_{e}\rbrack\). Clearly, we have that,

\[s\left( t_{b},t_{e} \right\rbrack = s\left( t_{e} \right) - s\left( t_{b} \right)\]

Define \(n(t_{b},t_{e}\rbrack\) as the count of the observations during the interval, \((t_{b},t_{e}\rbrack\). Clearly, we have that,

\[n\left( t_{b},t_{e} \right\rbrack = n\left( t_{e} \right) - n\left( t_{b} \right)\]

Finally, we have that the average during the interval, \((t_{b},t_{e}\rbrack\) as

\[\overline{x}\left( t_{b},t_{e} \right\rbrack = \frac{s\left( t_{b},t_{e} \right\rbrack}{n\left( t_{b},t_{e} \right\rbrack}\]

Thus, if during the simulation we can observe, \(s\left( t_{b},t_{e} \right\rbrack\) and \(n\left( t_{b},t_{e} \right\rbrack\), we can compute the average during a specific time interval. To do this in a simulation, we can schedule an event for time, \(t_{b}\), and observe, \(s\left( t_{b} \right)\) and \(n\left( t_{b} \right)\). Then, we can schedule an event for time, \(t_{e}\), and observe, \(s\left( t_{e} \right)\) and \(n\left( t_{e} \right)\). Once these values are captured, we can compute \(\overline{x}\left( t_{b},t_{e} \right\rbrack\). If we observe this quantity across multiple replications, we will have the average that occurs during the defined period.

So far, the discussion has been about tally-based data. The process is essentially the same for time-persistent data. Recall that a time-persistent variable typically takes on the form of a step function. For example, let \(y(t)\) represents the value of some state variable at any time \(t\). Here \(y(t)\) will take on constant values during intervals of time corresponding to when the state variable changes, for example. \(y(t)\) = {0, 1, 2, 3, …}. \(y(t)\) is a curve (a step function in this particular case) and we compute the time average over the interval \((t_{b},t_{e}\rbrack\).as follows.

\[\overline{y}\left( t_{b},t_{e} \right) = \frac{\int_{t_{b}}^{t_{e}}{y\left( t \right)\text{dt}}}{t_{e} - t_{b}}\]

Similar to the tally-based case, we can define the following notation. Let \(a\left( t \right)\) be the cumulative area under the state variable curve.

\[a\left( t \right) = \int_{0}^{t}{y\left( t \right)\text{dt}}\]

Define \(\overline{y}(t)\) as the cumulative average up to and including time \(t\), such that:

\[\overline{y}\left( t \right) = \frac{\int_{0}^{t}{y\left( t \right)\text{dt}}}{t} = \frac{a\left( t \right)}{t}\]

Thus, \(a\left( t \right) = t \times \overline{y}\left( t \right)\). So, if we have a function to compute \(\overline{y}\left( t \right)\) we have the ability to compute,

\[\overline{y}\left( t_{b},t_{e} \right) = \frac{\int_{t_{b}}^{t_{e}}{y\left( t \right)\text{dt}}}{t_{e} - t_{b}} = \frac{a\left( t_{e} \right) - a\left( t_{b} \right)}{t_{e} - t_{b}}\]

Again, a strategy of scheduling events for \(t_{b}\) and \(t_{e}\) can allow you to observe the required quantities at the beginning and end of the period and then observe the desired average.

The key to collecting the statistics on observation-based over an interval of time is the usage of the ResponseInterval class within the KSL. Using the previously defined notation, we can capture \(\overline{x}\left( t \right)\), \(\overline{y}\left( t \right)\), and \(n(t)\) via the within replication statistics of response variables.

The ResponseInterval class represents an interval of time over which statistical collection should be performed. An interval is specified by providing an interval start time and a duration. The duration must be finite and greater than zero.

Simulation responses in the form of instances of Response, TWResponse, and Counter instances can be added to the interval for observation. New responses are created and associated with each of the supplied responses. The new responses collect observations associated with the supplied responses only during the specified interval. In the case of response variables or time weighted variables, the average response during the interval is observed. In the case of counters, the total count during the interval is observed.

If the interval is not associated with a ResponseSchedule, the interval may be repeated. In which case, the statistics are collected across the intervals. A repeated interval starts immediately after the previous duration. Note that for Response instances that are observed, if there are no observations during the interval then the average response during the interval is undefined (and thus not observed). Therefore, interval statistics for Response instances are conditional on the occurrence of at least one observation. This is most relevant when the interval is repeated because intervals with no observations are not tabulated. For example, suppose that there are no students that use the MalMart recruiters during the first hour of operation, then we cannot compute an average for this interval. Suppose we observe 10 days of operation of the mixer and on 2 of the days, there were no students that used the MalMart recruiters during the first hour of operation. Then, instead of getting a sample average across 10 days, we will only get a sample average across 8 days. We cannot compute statistics over observations that do not exist.

A ResponseInterval permits collection of statistics over a specific interval, which might repeat. Often we want to collect statistics across many intervals according to some timed pattern. The ResponseSchedule class facilitates the modeling of this situation.

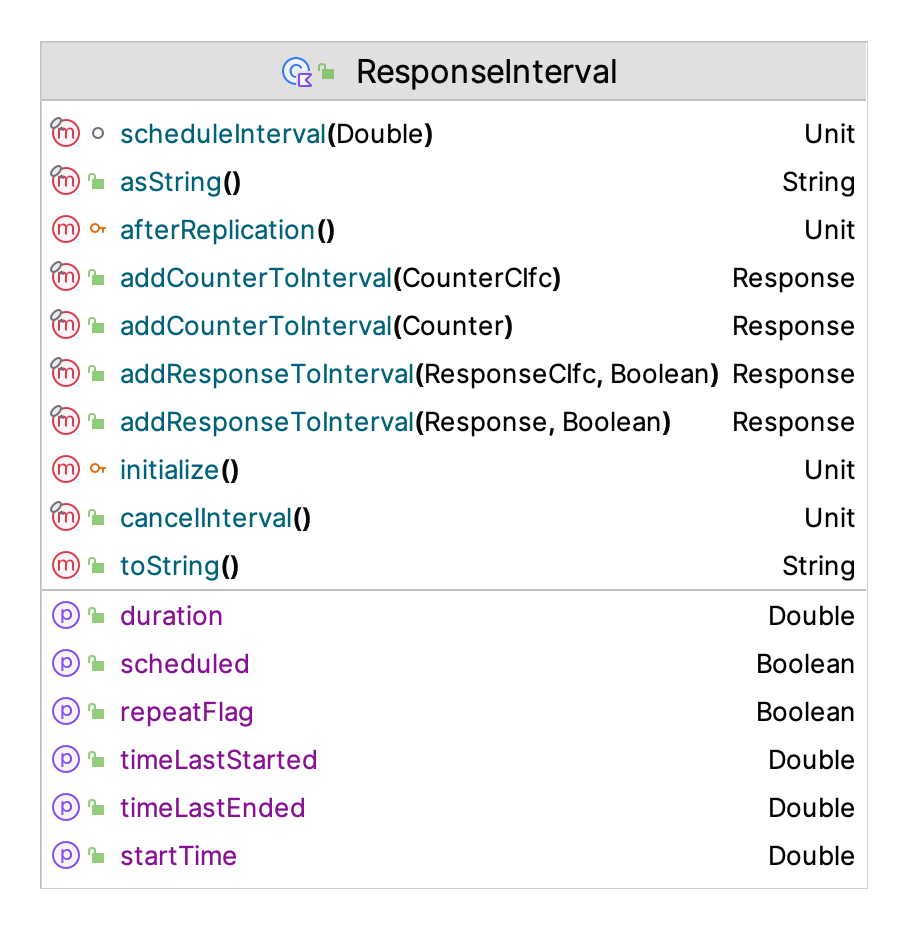
Figure 7.7: ResponseInterval Class

The ResponseSchedule class allows the creation of a schedule that represents a list of intervals of time. The starting length of a schedule is 0.0. The length of a schedule depends upon the intervals added to it. The schedule’s length encompasses the furthest interval added. If no intervals are added, then the schedule only has its start time and no response collection will occur.

The user adds intervals and responses for which statistics need to be collected during the intervals. The intervals within the cycle may overlap in time. The start time of an interval is specified relative to the beginning of the cycle. The length of any interval must be finite.

The schedule can be started any time after the start of the simulation. The default starting time of the schedule is time 0.0. The schedule will start automatically at the designated start time.

The schedule can be repeated after the cycle length of the schedule is reached. The default is for the schedule to automatically repeat. Note that depending on the simulation run length only a portion of the scheduled intervals may be executed.

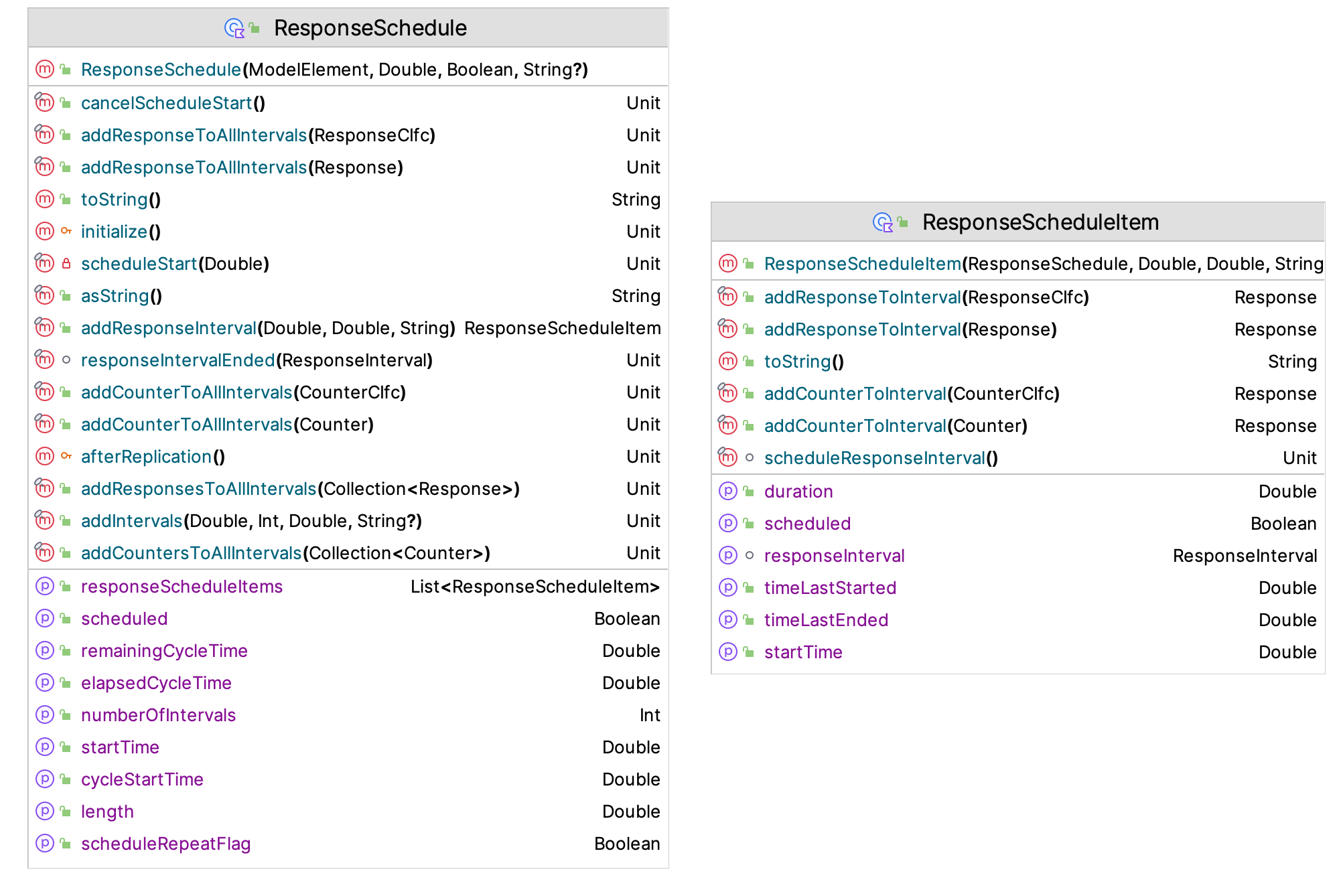
Figure 7.8: ResponseSchedule and ResponseScheduleItem Classes

The classic use case of this class is to collect statistics for each hour of the day. In this case, the user would use the addIntervals() method to add 24 intervals of 1 hour duration. Then responses (response variables, time weighted variables, and counters) can be added to the schedule. In which case, they will be added to each interval. Thus, interval statistics for each of the 24 intervals will be collected for every one of the added responses. If more than one day is simulated and the schedule is allowed to repeat, then statistics are collected across the days. That is, the statistics of hour 1 on day 1 are averaged with the statistics of hour 1 on all subsequent days. The following code illustrates the definition of a schedule to collect hourly responses for the STEM Fair Mixer situation.

    private val hourlyResponseSchedule = ResponseSchedule(this, 0.0, name = "Hourly")
    private val peakResponseInterval: ResponseInterval = ResponseInterval(this, 120.0, "PeakPeriod:[150.0,270.0]")

    init {
        hourlyResponseSchedule.scheduleRepeatFlag = false
        hourlyResponseSchedule.addIntervals(0.0, 6, 60.0)
        hourlyResponseSchedule.addResponseToAllIntervals(myJHBuntRecruiters.numBusyUnits)
        hourlyResponseSchedule.addResponseToAllIntervals(myMalWartRecruiters.numBusyUnits)
        hourlyResponseSchedule.addResponseToAllIntervals(myJHBuntRecruiters.waitingQ.timeInQ)
        hourlyResponseSchedule.addResponseToAllIntervals(myMalWartRecruiters.waitingQ.timeInQ)
        hourlyResponseSchedule.addResponseToAllIntervals(myJHBuntRecruiters.timeAvgInstantaneousUtil)
        hourlyResponseSchedule.addResponseToAllIntervals(myMalWartRecruiters.timeAvgInstantaneousUtil)
        peakResponseInterval.startTime = 150.0
        peakResponseInterval.addResponseToInterval(myTotalAtRecruiters)
        peakResponseInterval.addResponseToInterval(myJHBuntRecruiters.timeAvgInstantaneousUtil)
        peakResponseInterval.addResponseToInterval(myMalWartRecruiters.timeAvgInstantaneousUtil)
    }

In the code, an hourly response schedule is constructed and responses added to all the intervals. Access to specific intervals can be obtained and specific responses only added to specific intervals if needed. The code also illustrates the construction of a separate ResponseInterval and the adding of responses to it. Using a ResponseSchedule will result in many statistical quantities being defined. All the statistical responses will be automatically added to the summary statistical reports and captured within the KSL database (if used). The next section will overview the revisions to the STEM Mixer model to handle the non-stationary situation.

7.2.3.3 Implementing the Revised STEM Mixer Model

Since the STEM mixer model has been presented in a previous chapter, this section will focus on the aspects associated with the enhancements required for this chapter. Since the mixer can close with a warning time, we need variables to handle this situation.

class StemFairMixerEnhanced(parent: ModelElement, name: String? = null) : ProcessModel(parent, name) {

    var lengthOfMixer = 360.0
        set(value) {
            require(value > 0.0) { "The length of the mixer must be > 0.0" }
            field = value
        }
    var warningTime = 15.0
        set(value) {
            require(value > 0.0) { "The warning limit must be > 0.0" }
            field = value
        }

    val doorClosingTime
        get() = lengthOfMixer - warningTime

    var isClosed: Boolean = false
        private set

The length of the mixer can be varied and the length of the warning changed. The property isClosed will be used to indicate that students need to proceed to the exit. This situation involves the walking of the students. Thus, we need to specify the distances, velocity, and walking times. The following code defines the random variables needed for this modeling.

    private val myNameTagTimeRV = RandomVariable(this, UniformRV((15.0 / 60.0), (45.0 / 60.0), 2))
    private val myDecideToMix = RandomVariable(this, BernoulliRV(0.4, 3))
    private val myDecideToLeave = RandomVariable(this, BernoulliRV(0.1, 4))
    private val myInteractionTimeRV = RandomVariable(this, TriangularRV(10.0, 15.0, 30.0, 5))
    private val myDecideRecruiter = RandomVariable(this, BernoulliRV(0.5, 6))
    private val myTalkWithJHBunt = RandomVariable(this, ExponentialRV(6.0, 7))
    private val myTalkWithMalMart = RandomVariable(this, ExponentialRV(3.0, 8))
    private val myWalkingSpeedRV = TriangularRV(88.0, 176.0, 264.0, 9)

    private val walkToNameTags = RandomVariable(this, 20.0 / myWalkingSpeedRV)
    private val walkFromNameTagsToConversationArea = RandomVariable(this, 30.0 / myWalkingSpeedRV)
    private val walkFromNameTagsToRecruiting = RandomVariable(this, 80.0 / myWalkingSpeedRV)
    private val walkFromNameTagsToExit = RandomVariable(this, 140.0 / myWalkingSpeedRV)
    private val walkFromConversationAreaToRecruiting = RandomVariable(this, 50.0 / myWalkingSpeedRV)
    private val walkFromConversationAreaToExit = RandomVariable(this, 110.0 / myWalkingSpeedRV)
    private val walkFromRecruitingToExit = RandomVariable(this, 60.0 / myWalkingSpeedRV)

Notice that a random variable is used to defined the walking speed and that this random variable is subsequently used to define the time to walk random variable. Because the walking speed random variable, myWalkingSpeedRV implements the RVariableIfc interface, the expression 20.0 / myWalkingSpeedRV actually produces another instance of a RVariableIfc and it can be used within the RandomVariable instance of the model.

There are many base responses to be defined. Besides the overall system time, we can collect the system time based on the type of student and use an indicator response to capture the probability of completing the visit within 30 minutes.

    private val myOverallSystemTime = Response(this, "OverallSystemTime")
    private val myRecruitingOnlySystemTime = Response(this, "RecruitingOnlySystemTime")

    init {
        myRecruitingOnlySystemTime.attachIndicator({ x -> x <= 30.0 }, "P(Recruiting Only < 30 minutes)")
    }

    private val myMixingStudentSystemTime = Response(this, "MixingStudentSystemTime")
    private val myMixingAndLeavingSystemTime = Response(this, "MixingStudentThatLeavesSystemTime")
    private val myNumInSystem = TWResponse(this, "NumInSystem")
    private val myNumInConversationArea = TWResponse(this, "NumInConversationArea")

    private val myNumAtJHBuntAtClosing = Response(this, "NumAtJHBuntAtClosing")
    private val myNumAtMalWartAtClosing = Response(this, "NumAtMalWartAtClosing")
    private val myNumAtConversationAtClosing = Response(this, "NumAtConversationAtClosing")
    private val myNumInSystemAtClosing = Response(this, "NumInSystemAtClosing")

    private val myJHBuntRecruiters: ResourceWithQ = ResourceWithQ(this, capacity = 3, name = "JHBuntR")
    val JHBuntRecruiters: ResourceCIfc
        get() = myJHBuntRecruiters
    private val myMalWartRecruiters: ResourceWithQ = ResourceWithQ(this, capacity = 2, name = "MalWartR")
    val MalWartRecruiters: ResourceCIfc
        get() = myMalWartRecruiters

    private val myTotalAtRecruiters: AggregateTWResponse = AggregateTWResponse(this, "StudentsAtRecruiters")
    init {
        myTotalAtRecruiters.observe(myJHBuntRecruiters.numBusyUnits)
        myTotalAtRecruiters.observe(myJHBuntRecruiters.waitingQ.numInQ)
        myTotalAtRecruiters.observe(myMalWartRecruiters.numBusyUnits)
        myTotalAtRecruiters.observe(myMalWartRecruiters.waitingQ.numInQ)
    }

We also need to define new responses to capture what is going on at the close of the mixer. That is, when the warning occurs that the mixer is closing. Notice also that we use an aggregate response to collect the total number of students at both of the recruiters.

To model the non-stationary arrivals, we use a piecewise constant rate function to define a non-homogeneous Poisson process and an event generator to generate the students.

    private val myTBArrivals: NHPPTimeBtwEventRV

    init {
        // set up the generator
        val durations = doubleArrayOf(
            30.0, 30.0, 30.0, 30.0, 30.0, 30.0,
            30.0, 30.0, 30.0, 30.0, 30.0, 30.0
        )
        val hourlyRates = doubleArrayOf(
            5.0, 10.0, 15.0, 25.0, 40.0, 50.0,
            55.0, 55.0, 60.0, 30.0, 5.0, 5.0
        )
        val ratesPerMinute = hourlyRates.divideConstant(60.0)
        val f = PiecewiseConstantRateFunction(durations, ratesPerMinute)
        myTBArrivals = NHPPTimeBtwEventRV(this, f, streamNum = 1)
    }

    private val generator = EventGenerator(this, this::createStudents, myTBArrivals, myTBArrivals)

The interval responses are defined as previously discussed. We also define a response to capture when the mixer ends. Notice that the ResponseSchedule is told not to repeat. This is essential because we will not specify a replication run length for this model.

    private val hourlyResponseSchedule = ResponseSchedule(this, 0.0, name = "Hourly")
    private val peakResponseInterval: ResponseInterval = ResponseInterval(this, 120.0, "PeakPeriod:[150.0,270.0]")

    init {
        hourlyResponseSchedule.scheduleRepeatFlag = false
        hourlyResponseSchedule.addIntervals(0.0, 6, 60.0)
        hourlyResponseSchedule.addResponseToAllIntervals(myJHBuntRecruiters.numBusyUnits)
        hourlyResponseSchedule.addResponseToAllIntervals(myMalWartRecruiters.numBusyUnits)
        hourlyResponseSchedule.addResponseToAllIntervals(myJHBuntRecruiters.waitingQ.timeInQ)
        hourlyResponseSchedule.addResponseToAllIntervals(myMalWartRecruiters.waitingQ.timeInQ)
        hourlyResponseSchedule.addResponseToAllIntervals(myJHBuntRecruiters.timeAvgInstantaneousUtil)
        hourlyResponseSchedule.addResponseToAllIntervals(myMalWartRecruiters.timeAvgInstantaneousUtil)
        peakResponseInterval.startTime = 150.0
        peakResponseInterval.addResponseToInterval(myTotalAtRecruiters)
        peakResponseInterval.addResponseToInterval(myJHBuntRecruiters.timeAvgInstantaneousUtil)
        peakResponseInterval.addResponseToInterval(myMalWartRecruiters.timeAvgInstantaneousUtil)
    }

    private val myEndTime = Response(this, "Mixer Ending Time")
    init{
        myEndTime.attachIndicator({ x -> x > lengthOfMixer }, "Prob(EndTime>$lengthOfMixer)")
    }

At the start of the replication, we need to schedule the closing of the mixer at the appropriate time and activate the processes for the students.

    override fun initialize() {
        isClosed = false
        schedule(this::closeMixer, doorClosingTime)
    }

    override fun replicationEnded() {
        myEndTime.value = time
    }

    private fun createStudents(eventGenerator: EventGenerator) {
        val student = Student()
        if (student.isMixer) {
            activate(student.mixingStudentProcess)
        } else {
            activate(student.recruitingOnlyStudentProcess)
        }
    }

    private fun closeMixer(event: KSLEvent<Nothing>) {
        isClosed = true
        // turn off the generator
        generator.turnOffGenerator()
        // collect statistics
        myNumAtJHBuntAtClosing.value = myJHBuntRecruiters.waitingQ.numInQ.value + myJHBuntRecruiters.numBusy
        myNumAtMalWartAtClosing.value = myMalWartRecruiters.waitingQ.numInQ.value + myMalWartRecruiters.numBusy
        myNumAtConversationAtClosing.value = myNumInConversationArea.value
        myNumInSystemAtClosing.value = myNumInSystem.value
    }

The initialize() method is used to schedule the closing of the mixer. In the event action associated with the closing, we turn off the student generation process and we capture the required statistics about the state of the mixer at that time. Notice the action associated with the event generator. In this case, we are not using an entity generator so that we can activate the process associated with whether the student visits the conversation area or not.

Let’s first take a look at the process for those students that visit the conversation area. It is quite a lengthy process routine. In the following code, first we define two properties that capture whether the student mixes (isMixer) and whether they leave early (isLeaver). Then, the mixing student process is defined. In the definition, note that we do not add the process to the entity’s process sequence. This is because we will have another process (for non-mixing students) and we do not want the processes to automatically start. We controlled the starting of the processes within the event generator action.

    private inner class Student : Entity() {
        val isMixer = myDecideToMix.value.toBoolean()
        val isLeaver = myDecideToLeave.value.toBoolean()

        val mixingStudentProcess = process {
            myNumInSystem.increment()
            delay(walkToNameTags)
            // at name tag station
            if (isClosed) {
                // mixer closed during walking
                delay(walkFromNameTagsToExit)
                departMixer(this@Student)
            } else {
                // get name tags
                delay(myNameTagTimeRV)
                if (isClosed) {
                    // mixer closed during name tag
                    delay(walkFromNameTagsToExit)
                    departMixer(this@Student)
                } else {
                    // goto the conversation area
                    delay(walkFromNameTagsToConversationArea)
                    if (isClosed) {
                        // closed during walking, must leave
                        delay(walkFromConversationAreaToExit)
                        departMixer(this@Student)
                    } else {
                        // start the conversation
                        myNumInConversationArea.increment()
                        delay(myInteractionTimeRV)
                        myNumInConversationArea.decrement()
                        if (isClosed) {
                            // closed during conversation, must leave
                            delay(walkFromConversationAreaToExit)
                            departMixer(this@Student)
                        } else {
                            // decide to leave or go to recruiting
                            if (isLeaver) {
                                delay(walkFromConversationAreaToExit)
                                departMixer(this@Student)
                            } else {
                                delay(walkFromConversationAreaToRecruiting)
                                if (!isClosed) {
                                    // proceed with recruiting visit
                                    val firstRecruiter = decideRecruiter()
                                    if (firstRecruiter == myJHBuntRecruiters) {
                                        use(myJHBuntRecruiters, delayDuration = myTalkWithJHBunt)
                                        use(myMalWartRecruiters, delayDuration = myTalkWithMalMart)
                                    } else {
                                        use(myMalWartRecruiters, delayDuration = myTalkWithMalMart)
                                        use(myJHBuntRecruiters, delayDuration = myTalkWithJHBunt)
                                    }
                                }
                                // either closed or they visited recruiting
                                delay(walkFromRecruitingToExit)
                                departMixer(this@Student)
                            }
                        }
                    }
                }
            }
        }

The process description is lengthy but fairly self-explanatory. The key complicating factor is that after each delay (for walking, name tags, etc.), we need to check if the warning for the closing of the mixer has occurred. The long if-else constructs ensure that there is only one path through the process for those students that depart early or due to closing. Those students that depart are sent to the departMixer() method, which collects statistics. The process of visiting the recruiters is more complex than in the previous presentation. In this case, we use a function, decideRecruiter() that picks the first station to visit.

   private fun decideRecruiter(): ResourceWithQ {
        // check the equal case first to show no preference
        val j = myJHBuntRecruiters.waitingQ.size + myJHBuntRecruiters.numBusy
        val m = myMalWartRecruiters.waitingQ.size + myMalWartRecruiters.numBusy
        if (j == m ){
            if (myDecideRecruiter.value.toBoolean()) {
                return myJHBuntRecruiters
            } else {
                return myMalWartRecruiters
            }
        } else if (j < m) {
            return myJHBuntRecruiters
        } else  {
            // MalWart must be smaller
            return myMalWartRecruiters
        }
    }

The decideRecruiter() function compares the recruiting stations based on the number waiting and in service. If they are the same, we randomly pick between them; otherwise, we pick the recruiter that has less activity. To show no preference to either recruiter, it is important to first check the equality case. For example, if we were to select the recruiter with the least activity first, then whichever one we listed would be checked in the order of the if statement and thus a preference established. The process for the students that only visit the recruiting area is less complicated.

        val recruitingOnlyStudentProcess = process {
            myNumInSystem.increment()
            delay(walkToNameTags)
            // at name tag station
            if (isClosed) {
                // mixer closed during walking
                delay(walkFromNameTagsToExit)
                departMixer(this@Student)
            } else {
                delay(myNameTagTimeRV)
                if (isClosed) {
                    // mixer closed during name tag
                    delay(walkFromNameTagsToExit)
                    departMixer(this@Student)
                } else {
                    // proceed to recruiting
                    delay(walkFromNameTagsToRecruiting)
                    if (!isClosed) {
                        // proceed with recruiting visit
                        val firstRecruiter = decideRecruiter()
                        if (firstRecruiter == myJHBuntRecruiters) {
                            use(myJHBuntRecruiters, delayDuration = myTalkWithJHBunt)
                            use(myMalWartRecruiters, delayDuration = myTalkWithMalMart)
                        } else {
                            use(myMalWartRecruiters, delayDuration = myTalkWithMalMart)
                            use(myJHBuntRecruiters, delayDuration = myTalkWithJHBunt)
                        }
                    }
                    // either closed or they visited recruiting
                    delay(walkFromRecruitingToExit)
                    departMixer(this@Student)
                }
            }

As previously mentioned, the departMixer() function captures the statistics. We use the isMixer and isLeaver attributes to ensure the capture of system time for these types of students.

        private fun departMixer(departingStudent: Student) {
            myNumInSystem.decrement()
            val st = time - departingStudent.createTime
            myOverallSystemTime.value = st
            if (isMixer) {
                myMixingStudentSystemTime.value = st
                if (isLeaver) {
                    myMixingAndLeavingSystemTime.value = st
                }
            } else {
                myRecruitingOnlySystemTime.value = st
            }

        }

Now we are ready to run the base case of the mixer model before investigating the staffing and scheduling of the recruiters.

7.2.3.4 Running the Revised STEM Mixer Model

The base case assumes that the recruiters have the same capacity for the entire 6 hours of operation. The output from this model is quite lengthy. Notice that the response schedule collects statistics on the average during the interval for both the Response and TWResponse variables and the value of the variable at the start of the interval for TWResponse variables. There are a few items to note:

The overall system time is quite high.
The number of students at the recruiting area is high when the warning occurs, especially at the JHBunt recruiters with more than 35 students on average.
The utilization of the recruiters over the entire time frame is very reasonable, 0.7838 and 0.5908 for the JHBunt and MalWart recruiters, respectively.
The number of busy recruiters gets excessively high during the peak period, with the utilization averaging 99% for both recruiters.
We see that the mixer ends substantially after the closing time.

The non-stationary aspects of this situation definitely have an effect on the performance. The hourly performance is especially helpful to understand this situation. If we only had the average performance over the entire time, we might be fooled into thinking that the capacity of the recruiters was not a problem.

Base Case Statistical Summary Report

Name	Count	Average	Half-Width
OverallSystemTime	400	65.9	1.495
RecruitingOnlySystemTime	400	58.287	1.486
P(Recruiting Only < 30 minutes)	400	0.341	0.011
MixingStudentSystemTime	400	77.295	1.586
MixingStudentThatLeavesSystemTime	400	19.738	0.167
NumInSystem	400	27.092	0.569
NumInConversationArea	400	3.033	0.034
NumAtJHBuntAtClosing	400	35.618	1.232
NumAtMalWartAtClosing	400	8.057	0.827
NumAtConversationAtClosing	400	0.635	0.077
NumInSystemAtClosing	400	44.615	1.601
JHBuntR:InstantaneousUtil	400	0.785	0.004
JHBuntR:NumBusyUnits	400	2.356	0.011
JHBuntR:ScheduledUtil	400	0.785	0.004
JHBuntR:WIP	400	15.739	0.422
JHBuntR:Q:NumInQ	400	13.384	0.417
JHBuntR:Q:TimeInQ	400	34.2	1.164
MalWartR:InstantaneousUtil	400	0.595	0.006
MalWartR:NumBusyUnits	400	1.191	0.011
MalWartR:ScheduledUtil	400	0.595	0.006
MalWartR:WIP	400	7.72	0.257
MalWartR:Q:NumInQ	400	6.529	0.251
MalWartR:Q:TimeInQ	400	16.474	0.614
StudentsAtRecruiters	400	23.459	0.571
JHBuntR:NumBusyUnits:IntervalAvg:Hourly:01:[0_0,60_0]	400	0.455	0.028
JHBuntR:NumBusyUnits:ValueAtStart:Hourly:01:[0_0,60_0]	400	0	0
JHBuntR:NumBusyUnits:IntervalAvg:Hourly:02:[60_0,120_0]	400	1.396	0.046
JHBuntR:NumBusyUnits:ValueAtStart:Hourly:02:[60_0,120_0]	400	0.818	0.083
JHBuntR:NumBusyUnits:IntervalAvg:Hourly:03:[120_0,180_0]	400	2.716	0.029
JHBuntR:NumBusyUnits:ValueAtStart:Hourly:03:[120_0,180_0]	400	2.165	0.097
JHBuntR:NumBusyUnits:IntervalAvg:Hourly:04:[180_0,240_0]	400	2.996	0.002
JHBuntR:NumBusyUnits:ValueAtStart:Hourly:04:[180_0,240_0]	400	2.983	0.015
JHBuntR:NumBusyUnits:IntervalAvg:Hourly:05:[240_0,300_0]	400	3	0
JHBuntR:NumBusyUnits:ValueAtStart:Hourly:05:[240_0,300_0]	400	3	0
JHBuntR:NumBusyUnits:IntervalAvg:Hourly:06:[300_0,360_0]	400	2.998	0.002
JHBuntR:NumBusyUnits:ValueAtStart:Hourly:06:[300_0,360_0]	400	3	0
MalWartR:NumBusyUnits:IntervalAvg:Hourly:01:[0_0,60_0]	400	0.25	0.014
MalWartR:NumBusyUnits:ValueAtStart:Hourly:01:[0_0,60_0]	400	0	0
MalWartR:NumBusyUnits:IntervalAvg:Hourly:02:[60_0,120_0]	400	0.755	0.026
MalWartR:NumBusyUnits:ValueAtStart:Hourly:02:[60_0,120_0]	400	0.465	0.064
MalWartR:NumBusyUnits:IntervalAvg:Hourly:03:[120_0,180_0]	400	1.638	0.025
MalWartR:NumBusyUnits:ValueAtStart:Hourly:03:[120_0,180_0]	400	1.152	0.077
MalWartR:NumBusyUnits:IntervalAvg:Hourly:04:[180_0,240_0]	400	1.976	0.006
MalWartR:NumBusyUnits:ValueAtStart:Hourly:04:[180_0,240_0]	400	1.92	0.032
MalWartR:NumBusyUnits:IntervalAvg:Hourly:05:[240_0,300_0]	400	1.997	0.003
MalWartR:NumBusyUnits:ValueAtStart:Hourly:05:[240_0,300_0]	400	1.995	0.007
MalWartR:NumBusyUnits:IntervalAvg:Hourly:06:[300_0,360_0]	400	1.834	0.03
MalWartR:NumBusyUnits:ValueAtStart:Hourly:06:[300_0,360_0]	400	1.982	0.016
JHBuntR:Q:TimeInQ:IntervalAvg:Hourly:01:[0_0,60_0]	399	0.04	0.023
JHBuntR:Q:TimeInQ:IntervalAvg:Hourly:02:[60_0,120_0]	400	0.557	0.098
JHBuntR:Q:TimeInQ:IntervalAvg:Hourly:03:[120_0,180_0]	400	5.856	0.376
JHBuntR:Q:TimeInQ:IntervalAvg:Hourly:04:[180_0,240_0]	400	20.507	0.776
JHBuntR:Q:TimeInQ:IntervalAvg:Hourly:05:[240_0,300_0]	400	38.733	1.04
JHBuntR:Q:TimeInQ:IntervalAvg:Hourly:06:[300_0,360_0]	400	56.158	1.319
MalWartR:Q:TimeInQ:IntervalAvg:Hourly:01:[0_0,60_0]	399	0.03	0.013
MalWartR:Q:TimeInQ:IntervalAvg:Hourly:02:[60_0,120_0]	400	0.324	0.046
MalWartR:Q:TimeInQ:IntervalAvg:Hourly:03:[120_0,180_0]	400	3.524	0.247
MalWartR:Q:TimeInQ:IntervalAvg:Hourly:04:[180_0,240_0]	400	12.886	0.572
MalWartR:Q:TimeInQ:IntervalAvg:Hourly:05:[240_0,300_0]	400	26.028	0.843
MalWartR:Q:TimeInQ:IntervalAvg:Hourly:06:[300_0,360_0]	400	31.864	1.39
JHBuntR:InstantaneousUtil:IntervalAvg:Hourly:01:[0_0,60_0]	400	0.152	0.009
JHBuntR:InstantaneousUtil:ValueAtStart:Hourly:01:[0_0,60_0]	400	0	0
JHBuntR:InstantaneousUtil:IntervalAvg:Hourly:02:[60_0,120_0]	400	0.465	0.015
JHBuntR:InstantaneousUtil:ValueAtStart:Hourly:02:[60_0,120_0]	400	0.272	0.028
JHBuntR:InstantaneousUtil:IntervalAvg:Hourly:03:[120_0,180_0]	400	0.905	0.01
JHBuntR:InstantaneousUtil:ValueAtStart:Hourly:03:[120_0,180_0]	400	0.722	0.032
JHBuntR:InstantaneousUtil:IntervalAvg:Hourly:04:[180_0,240_0]	400	0.999	0.001
JHBuntR:InstantaneousUtil:ValueAtStart:Hourly:04:[180_0,240_0]	400	0.994	0.005
JHBuntR:InstantaneousUtil:IntervalAvg:Hourly:05:[240_0,300_0]	400	1	0
JHBuntR:InstantaneousUtil:ValueAtStart:Hourly:05:[240_0,300_0]	400	1	0
JHBuntR:InstantaneousUtil:IntervalAvg:Hourly:06:[300_0,360_0]	400	0.999	0.001
JHBuntR:InstantaneousUtil:ValueAtStart:Hourly:06:[300_0,360_0]	400	1	0
MalWartR:InstantaneousUtil:IntervalAvg:Hourly:01:[0_0,60_0]	400	0.125	0.007
MalWartR:InstantaneousUtil:ValueAtStart:Hourly:01:[0_0,60_0]	400	0	0
MalWartR:InstantaneousUtil:IntervalAvg:Hourly:02:[60_0,120_0]	400	0.378	0.013
MalWartR:InstantaneousUtil:ValueAtStart:Hourly:02:[60_0,120_0]	400	0.232	0.032
MalWartR:InstantaneousUtil:IntervalAvg:Hourly:03:[120_0,180_0]	400	0.819	0.012
MalWartR:InstantaneousUtil:ValueAtStart:Hourly:03:[120_0,180_0]	400	0.576	0.039
MalWartR:InstantaneousUtil:IntervalAvg:Hourly:04:[180_0,240_0]	400	0.988	0.003
MalWartR:InstantaneousUtil:ValueAtStart:Hourly:04:[180_0,240_0]	400	0.96	0.016
MalWartR:InstantaneousUtil:IntervalAvg:Hourly:05:[240_0,300_0]	400	0.998	0.001
MalWartR:InstantaneousUtil:ValueAtStart:Hourly:05:[240_0,300_0]	400	0.998	0.003
MalWartR:InstantaneousUtil:IntervalAvg:Hourly:06:[300_0,360_0]	400	0.917	0.015
MalWartR:InstantaneousUtil:ValueAtStart:Hourly:06:[300_0,360_0]	400	0.991	0.008
StudentsAtRecruiters:IntervalAvg:PeakPeriod:[150_0,270_0]	400	30.891	0.809
StudentsAtRecruiters:ValueAtStart:PeakPeriod:[150_0,270_0]	400	9.905	0.494
JHBuntR:InstantaneousUtil:IntervalAvg:PeakPeriod:[150_0,270_0]	400	0.992	0.002
JHBuntR:InstantaneousUtil:ValueAtStart:PeakPeriod:[150_0,270_0]	400	0.94	0.017
MalWartR:InstantaneousUtil:IntervalAvg:PeakPeriod:[150_0,270_0]	400	0.971	0.004
MalWartR:InstantaneousUtil:ValueAtStart:PeakPeriod:[150_0,270_0]	400	0.85	0.029
Mixer Ending Time	400	430.291	3.258
Prob(EndTime>360_0)	400	0.998	0.005
JHBuntR:SeizeCount	400	169.798	1.25
MalWartR:SeizeCount	400	169.798	1.25

To further investigate this situation, the same model was run but with the capacity of the resources set at infinity. This will cause no queueing to occur, but will indicate the number of busy resources by hour of the day. This can help in specifying the required staffing. In the following results, only the critical performance measures are presented.

Infinite Capacity Statistical Summary Report

Name	Count	Average	Half-Width
OverallSystemTime	400	17.389	0.082
JHBuntR:NumBusyUnits:IntervalAvg:Hourly:01:[0_0,60_0]	400	0.458	0.029
JHBuntR:NumBusyUnits:IntervalAvg:Hourly:02:[60_0,120_0]	400	1.456	0.051
JHBuntR:NumBusyUnits:IntervalAvg:Hourly:03:[120_0,180_0]	400	3.693	0.08
JHBuntR:NumBusyUnits:IntervalAvg:Hourly:04:[180_0,240_0]	400	5.115	0.092
JHBuntR:NumBusyUnits:IntervalAvg:Hourly:05:[240_0,300_0]	400	4.973	0.095
JHBuntR:NumBusyUnits:IntervalAvg:Hourly:06:[300_0,360_0]	400	1.62	0.064
MalWartR:NumBusyUnits:IntervalAvg:Hourly:01:[0_0,60_0]	400	0.252	0.015
MalWartR:NumBusyUnits:IntervalAvg:Hourly:02:[60_0,120_0]	400	0.773	0.027
MalWartR:NumBusyUnits:IntervalAvg:Hourly:03:[120_0,180_0]	400	1.961	0.044
MalWartR:NumBusyUnits:IntervalAvg:Hourly:04:[180_0,240_0]	400	2.618	0.047
MalWartR:NumBusyUnits:IntervalAvg:Hourly:05:[240_0,300_0]	400	2.407	0.046
MalWartR:NumBusyUnits:IntervalAvg:Hourly:06:[300_0,360_0]	400	0.716	0.034
JHBuntR:InstantaneousUtil:IntervalAvg:Hourly:01:[0_0,60_0]	400	0	0
JHBuntR:InstantaneousUtil:IntervalAvg:Hourly:02:[60_0,120_0]	400	0	0
JHBuntR:InstantaneousUtil:IntervalAvg:Hourly:03:[120_0,180_0]	400	0	0
JHBuntR:InstantaneousUtil:IntervalAvg:Hourly:04:[180_0,240_0]	400	0	0
JHBuntR:InstantaneousUtil:IntervalAvg:Hourly:05:[240_0,300_0]	400	0	0
JHBuntR:InstantaneousUtil:IntervalAvg:Hourly:06:[300_0,360_0]	400	0	0
MalWartR:InstantaneousUtil:IntervalAvg:Hourly:01:[0_0,60_0]	400	0	0
MalWartR:InstantaneousUtil:IntervalAvg:Hourly:02:[60_0,120_0]	400	0	0
MalWartR:InstantaneousUtil:IntervalAvg:Hourly:03:[120_0,180_0]	400	0	0
MalWartR:InstantaneousUtil:IntervalAvg:Hourly:04:[180_0,240_0]	400	0	0
MalWartR:InstantaneousUtil:IntervalAvg:Hourly:05:[240_0,300_0]	400	0	0
MalWartR:InstantaneousUtil:IntervalAvg:Hourly:06:[300_0,360_0]	400	0	0
Mixer Ending Time	400	363.773	0.699
Prob(EndTime>360_0)	400	0.427	0.049

The results of running the non-stationary arrival schedule with infinite capacity for the recruiting resources indicate the effect on the resources. Notice how the estimated number busy units for the resources track the arrival pattern. Now considering the JHBunt recruiting station during the fourth hour of the day, we see an average number of recruiters busy of 5.128. Thus, if we set the resource capacity of the JHBunt recruiting station to 6 recruiters during the fourth hour of the day, we would expect to achieve a utilization of about 88%, (\(5.128/6 = 0.8547\)). With this thinking in mind we can determine the required capacity for each hour of the day and the expected utilization.

With these results in mind, we can develop a capacity schedule for this situation. The following code illustrates the creation of two schedules, one for controlling the JHBunt resource and one for controlling the MalMart resource. The capacity increases each hour until the last hour of the mixer.

    private val myJHBuntSchedule : CapacitySchedule = CapacitySchedule(this, 0.0)
    private val myMalWartSchedule : CapacitySchedule = CapacitySchedule(this, 0.0)

    init {

        myJHBuntSchedule.addItem(capacity = 1, duration = 60.0)
        myJHBuntSchedule.addItem(capacity = 2, duration = 60.0)
        myJHBuntSchedule.addItem(capacity = 4, duration = 60.0)
        myJHBuntSchedule.addItem(capacity = 7, duration = 60.0)
        myJHBuntSchedule.addItem(capacity = 7, duration = 60.0)
        myJHBuntSchedule.addItem(capacity = 3, duration = 60.0)
        myJHBuntRecruiters.useSchedule(myJHBuntSchedule, CapacityChangeRule.WAIT)

        myMalWartSchedule.addItem(capacity = 1, duration = 60.0)
        myMalWartSchedule.addItem(capacity = 2, duration = 60.0)
        myMalWartSchedule.addItem(capacity = 4, duration = 60.0)
        myMalWartSchedule.addItem(capacity = 6, duration = 60.0)
        myMalWartSchedule.addItem(capacity = 6, duration = 60.0)
        myMalWartSchedule.addItem(capacity = 3, duration = 60.0)
        myMalWartRecruiters.useSchedule(myMalWartSchedule, CapacityChangeRule.WAIT)

    }

A portion of the results are shown here. Notice that when using a capacity schedule that additional statistics on the time spent in the busy, idle, and inactive states are collected. The hourly responses for number busy and utilization are more realistic and the utilization during the peak is very much within a reasonable range of operation. However, the chance that the mixer goes over the planned time is still quite high. The reader is asked to suggest ways to address this situation within the exercises.

Scheduled Capacity Statistical Summary Report

Name	Count	Average	Half-Width
OverallSystemTime	400	19.939	0.241
RecruitingOnlySystemTime	400	13.179	0.25
P(Recruiting Only < 30 minutes)	400	0.958	0.005
MixingStudentSystemTime	400	30.054	0.24
MixingStudentThatLeavesSystemTime	400	19.766	0.166
NumInSystem	400	9.696	0.155
NumInConversationArea	400	3.558	0.042
NumAtJHBuntAtClosing	400	1.137	0.173
NumAtMalWartAtClosing	400	0.357	0.057
NumAtConversationAtClosing	400	0.678	0.081
NumInSystemAtClosing	400	2.315	0.206
JHBuntR:PTimeInactive	400	0	0
JHBuntR:PTimeIdle	400	0.224	0.005
JHBuntR:PTimeBusy	400	0.776	0.005
JHBuntR:InstantaneousUtil	400	0.621	0.007
JHBuntR:NumActiveUnits	400	4.008	0.002
JHBuntR:NumBusyUnits	400	2.773	0.028
JHBuntR:ScheduledUtil	400	0.692	0.007
JHBuntR:WIP	400	3.974	0.127
JHBuntR:Q:NumInQ	400	1.201	0.107
JHBuntR:Q:TimeInQ	400	2.53	0.215
MalWartR:PTimeInactive	400	0	0
MalWartR:PTimeIdle	400	0.369	0.004
MalWartR:PTimeBusy	400	0.631	0.004
MalWartR:InstantaneousUtil	400	0.348	0.004
MalWartR:NumActiveUnits	400	3.661	0.001
MalWartR:NumBusyUnits	400	1.396	0.014
MalWartR:ScheduledUtil	400	0.381	0.004
MalWartR:WIP	400	1.46	0.017
MalWartR:Q:NumInQ	400	0.064	0.006
MalWartR:Q:TimeInQ	400	0.135	0.012
StudentsAtRecruiters	400	5.434	0.135
JHBuntR:NumBusyUnits:IntervalAvg:Hourly:01:[0_0,60_0]	400	0.388	0.02
JHBuntR:NumBusyUnits:ValueAtStart:Hourly:01:[0_0,60_0]	400	0	0
JHBuntR:NumBusyUnits:IntervalAvg:Hourly:02:[60_0,120_0]	400	1.339	0.037
JHBuntR:NumBusyUnits:ValueAtStart:Hourly:02:[60_0,120_0]	400	1.072	0.085
JHBuntR:NumBusyUnits:IntervalAvg:Hourly:03:[120_0,180_0]	400	3.395	0.049
JHBuntR:NumBusyUnits:ValueAtStart:Hourly:03:[120_0,180_0]	400	2.983	0.122
JHBuntR:NumBusyUnits:IntervalAvg:Hourly:04:[180_0,240_0]	400	5.52	0.091
JHBuntR:NumBusyUnits:ValueAtStart:Hourly:04:[180_0,240_0]	400	5.92	0.171
JHBuntR:NumBusyUnits:IntervalAvg:Hourly:05:[240_0,300_0]	400	5.069	0.091
JHBuntR:NumBusyUnits:ValueAtStart:Hourly:05:[240_0,300_0]	400	5.303	0.177
JHBuntR:NumBusyUnits:IntervalAvg:Hourly:06:[300_0,360_0]	400	1.884	0.068
JHBuntR:NumBusyUnits:ValueAtStart:Hourly:06:[300_0,360_0]	400	3.555	0.182
MalWartR:NumBusyUnits:IntervalAvg:Hourly:01:[0_0,60_0]	400	0.241	0.013
MalWartR:NumBusyUnits:ValueAtStart:Hourly:01:[0_0,60_0]	400	0	0
MalWartR:NumBusyUnits:IntervalAvg:Hourly:02:[60_0,120_0]	400	0.776	0.027
MalWartR:NumBusyUnits:ValueAtStart:Hourly:02:[60_0,120_0]	400	0.603	0.074
MalWartR:NumBusyUnits:IntervalAvg:Hourly:03:[120_0,180_0]	400	1.979	0.043
MalWartR:NumBusyUnits:ValueAtStart:Hourly:03:[120_0,180_0]	400	1.48	0.122
MalWartR:NumBusyUnits:IntervalAvg:Hourly:04:[180_0,240_0]	400	2.626	0.048
MalWartR:NumBusyUnits:ValueAtStart:Hourly:04:[180_0,240_0]	400	2.67	0.166
MalWartR:NumBusyUnits:IntervalAvg:Hourly:05:[240_0,300_0]	400	2.403	0.046
MalWartR:NumBusyUnits:ValueAtStart:Hourly:05:[240_0,300_0]	400	2.692	0.144
MalWartR:NumBusyUnits:IntervalAvg:Hourly:06:[300_0,360_0]	400	0.848	0.041
MalWartR:NumBusyUnits:ValueAtStart:Hourly:06:[300_0,360_0]	400	1.452	0.111
JHBuntR:Q:TimeInQ:IntervalAvg:Hourly:01:[0_0,60_0]	399	2.221	0.291
JHBuntR:Q:TimeInQ:IntervalAvg:Hourly:02:[60_0,120_0]	400	3.317	0.361
JHBuntR:Q:TimeInQ:IntervalAvg:Hourly:03:[120_0,180_0]	400	4.105	0.368
JHBuntR:Q:TimeInQ:IntervalAvg:Hourly:04:[180_0,240_0]	400	2.196	0.305
JHBuntR:Q:TimeInQ:IntervalAvg:Hourly:05:[240_0,300_0]	400	1.327	0.237
JHBuntR:Q:TimeInQ:IntervalAvg:Hourly:06:[300_0,360_0]	399	1.396	0.385
MalWartR:Q:TimeInQ:IntervalAvg:Hourly:01:[0_0,60_0]	399	0.604	0.102
MalWartR:Q:TimeInQ:IntervalAvg:Hourly:02:[60_0,120_0]	400	0.377	0.048
MalWartR:Q:TimeInQ:IntervalAvg:Hourly:03:[120_0,180_0]	400	0.195	0.032
MalWartR:Q:TimeInQ:IntervalAvg:Hourly:04:[180_0,240_0]	400	0.034	0.009
MalWartR:Q:TimeInQ:IntervalAvg:Hourly:05:[240_0,300_0]	400	0.022	0.007
MalWartR:Q:TimeInQ:IntervalAvg:Hourly:06:[300_0,360_0]	398	0.03	0.012
JHBuntR:InstantaneousUtil:IntervalAvg:Hourly:01:[0_0,60_0]	400	0.38	0.02
JHBuntR:InstantaneousUtil:ValueAtStart:Hourly:01:[0_0,60_0]	400	0	0
JHBuntR:InstantaneousUtil:IntervalAvg:Hourly:02:[60_0,120_0]	400	0.696	0.017
JHBuntR:InstantaneousUtil:ValueAtStart:Hourly:02:[60_0,120_0]	400	0.536	0.042
JHBuntR:InstantaneousUtil:IntervalAvg:Hourly:03:[120_0,180_0]	400	0.852	0.012
JHBuntR:InstantaneousUtil:ValueAtStart:Hourly:03:[120_0,180_0]	400	0.746	0.031
JHBuntR:InstantaneousUtil:IntervalAvg:Hourly:04:[180_0,240_0]	400	0.789	0.013
JHBuntR:InstantaneousUtil:ValueAtStart:Hourly:04:[180_0,240_0]	400	0.846	0.024
JHBuntR:InstantaneousUtil:IntervalAvg:Hourly:05:[240_0,300_0]	400	0.72	0.013
JHBuntR:InstantaneousUtil:ValueAtStart:Hourly:05:[240_0,300_0]	400	0.757	0.025
JHBuntR:InstantaneousUtil:IntervalAvg:Hourly:06:[300_0,360_0]	400	0.566	0.019
JHBuntR:InstantaneousUtil:ValueAtStart:Hourly:06:[300_0,360_0]	400	0.724	0.024
MalWartR:InstantaneousUtil:IntervalAvg:Hourly:01:[0_0,60_0]	400	0.235	0.013
MalWartR:InstantaneousUtil:ValueAtStart:Hourly:01:[0_0,60_0]	400	0	0
MalWartR:InstantaneousUtil:IntervalAvg:Hourly:02:[60_0,120_0]	400	0.41	0.013
MalWartR:InstantaneousUtil:ValueAtStart:Hourly:02:[60_0,120_0]	400	0.301	0.037
MalWartR:InstantaneousUtil:IntervalAvg:Hourly:03:[120_0,180_0]	400	0.5	0.011
MalWartR:InstantaneousUtil:ValueAtStart:Hourly:03:[120_0,180_0]	400	0.37	0.031
MalWartR:InstantaneousUtil:IntervalAvg:Hourly:04:[180_0,240_0]	400	0.439	0.008
MalWartR:InstantaneousUtil:ValueAtStart:Hourly:04:[180_0,240_0]	400	0.445	0.028
MalWartR:InstantaneousUtil:IntervalAvg:Hourly:05:[240_0,300_0]	400	0.396	0.008
MalWartR:InstantaneousUtil:ValueAtStart:Hourly:05:[240_0,300_0]	400	0.449	0.024
MalWartR:InstantaneousUtil:IntervalAvg:Hourly:06:[300_0,360_0]	400	0.277	0.013
MalWartR:InstantaneousUtil:ValueAtStart:Hourly:06:[300_0,360_0]	400	0.452	0.031
StudentsAtRecruiters:IntervalAvg:PeakPeriod:[150_0,270_0]	400	9.985	0.3
StudentsAtRecruiters:ValueAtStart:PeakPeriod:[150_0,270_0]	400	7.843	0.416
JHBuntR:InstantaneousUtil:IntervalAvg:PeakPeriod:[150_0,270_0]	400	0.818	0.009
JHBuntR:InstantaneousUtil:ValueAtStart:PeakPeriod:[150_0,270_0]	400	0.867	0.022
MalWartR:InstantaneousUtil:IntervalAvg:PeakPeriod:[150_0,270_0]	400	0.476	0.006
MalWartR:InstantaneousUtil:ValueAtStart:PeakPeriod:[150_0,270_0]	400	0.481	0.03
Mixer Ending Time	400	363.422	0.487
Prob(EndTime>360_0)	400	0.505	0.049
JHBuntR:SeizeCount	400	168.56	1.244
MalWartR:SeizeCount	400	168.56	1.244

Non-stationary arrival patterns are a fact of life in many systems that handle people. The natural daily processes of waking up, working, etc. all contribute to processes that depend on time. This section illustrated how to model non-stationary arrival processes and illustrated some of the concepts necessary when developing staffing plans for such systems. Incorporating these modeling issues into your simulation models allows for more realistic analysis; however, this also necessitates much more complex statistical analysis of the input distributions and requires careful capture of meaningful statistics. Capturing statistics by time periods is especially important because the statistical results that do not account for the time varying nature of the performance measures may mask what may be actually happening within the model. The overall average across the entire simulation time horizon may be significantly different than what occurs during individual periods of time that correspond to non-stationary situations. A good design must reflect these variations due to time.

In the next section, we continue the exploration of advanced process modeling techniques by illustrating how to model the balking and reneging of entities within queues.

G References

Leemis, L. M., and S. K. Park. 2006. Discrete-Event Simulation: A First Course. Prentice-Hall.

Ross, S. 1997. Introduction to Probability Models. 6th ed. Academic Press.