5.5 Applying Queueing Theory Results to Verify and Validate a Simulation
In this section, we overview some verification and validation methods to apply when developing and testing a simulation model.
Verification is about checking if the model meets the desired output. In other words, does the model work correctly as designed? In verifying a model, you select a sample of test cases with known results and show that the model produces the expected output across the test cases. It is important to select the test cases in an unbiased manner and that the test cases encompass a large portion of the space that will be relevant when using the model. The test cases form the standard that the model must meet and thus are critical in convincing others that the verification process was of high quality.
Validation is whether or not the model meets it intended purpose. When validating a model, we are trying to build credibility that the model can be used as intended. In other words, that the model adequately represents the system for its intended purpose. Obviously, verification is a necessary but not sufficient step in validation. Validation is predicated on how the model is intended to be used and what it is supposed to represent.
In the following, we will illustrate a basic approach to verifying and validating the results of a simulation model by using some analytical approximations based on queueing theory and common sense. Let’s start with an example system to be simulated.
Example 5.1 (Small Manufacturing System) A small manufacturing system produces parts. The parts arrive from an upstream Poisson process with a rate of arrival of 1 part every 5 minutes. All parts that enter the system must go through a preparation station where there are 2 preparation workers. A part requires only 1 of the 2 workers during preparation. The preparation time is exponentially distributed with means of 8 minutes. If all the workers at the preparation station are busy, then the part waits for the next available preparation worker.
After preparation, the parts are processed on two different production lines. There is a 30% chance that the parts are built on line 1 and a 70% chance that they go to line 2. Line 1 has a build station staffed by 2 workers. Line 2 has a build station staffed by 3 workers. The time to build a part on line 1 is triangularly distributed with a (min = 2, mode = 6, max = 8) minutes. The time to build a part on line 2 is triangularly distributed with a (min = 3, mode = 6, max = 7) minutes. The build operation on the part only requires 1 of the workers available at the station. If all the workers at the station are busy, then the part waits for the next available worker.
After the parts are built, they go to a packaging station. The packaging station is staffed by 2 workers. Only 1 of the 2 workers is needed during packaging. If all the workers at the packaging station are busy, then the part waits for the next available packaging worker. The time to individually wrap a part is exponential with a mean of 2 minutes. After each individual part is wrapped, the worker fills a box with packing peanuts, and places the part into a box for shipping. The time to fill the box with peanuts and seal the box is uniformly distribution between 1 and 2 minutes. After the packaging, the box is placed on a pallet building machine. Once 10 boxes accumulate, the pallet machine wraps the pallet. The wrapping time takes 2 minutes. After the wrapping is completed, the pallet leaves the system.
The production team believes that a batch run of production over 30 days of operation is the best way to produce these parts. Thus, at the beginning of a month there are currently no parts in production. Simulate the system for 100 replications of one month (30 days) of operation. The base time unit for the simulation should be in minutes. We want to simulate this system in order to measure the following performance metrics with some high degree of confidence.
| Performance Measures |
|---|
| System time for parts regardless of which build line prior to palletizer |
| Prob. that the system time before palletizing of a part is less than 60 minutes |
| Utilization of preparation workers |
| Utilization of packaging workers |
| Utilization of line 1 build workers |
| Utilization of line 2 build workers |
| Utilization of the palletizer |
| Total number of parts produced in 30 days |
| Total number of pallets completed in 30 days |
Suppose you build a simulation model for this situation and get the following results. The building of the model is left as an exercise for the reader.
| Performance Measures | Average | Half-width |
|---|---|---|
| System time for parts regardless of which build line prior to palletizer | 31.73 | 0.44 |
| Prob. that the system time before palletizing of a part is less than 60 minutes | 0.89 | 0.01 |
| Utilization of preparation workers | 0.80 | 0.00 |
| Utilization of packaging workers | 0.35 | 0.00 |
| Utilization of line 1 build workers | 0.16 | 0.00 |
| Utilization of line 2 build workers | 0.25 | 0.00 |
| Utilization of the palletizer | 0.039 | 0.00 |
| Total number of parts produced in 30 days | 8623.36 | 17.75 |
| Total number of pallets completed in 30 days | 861.85 | 1.77 |
How do you know if these results seem reasonable? You can use basic queueing analysis and some simple math to help verify and validate your results.
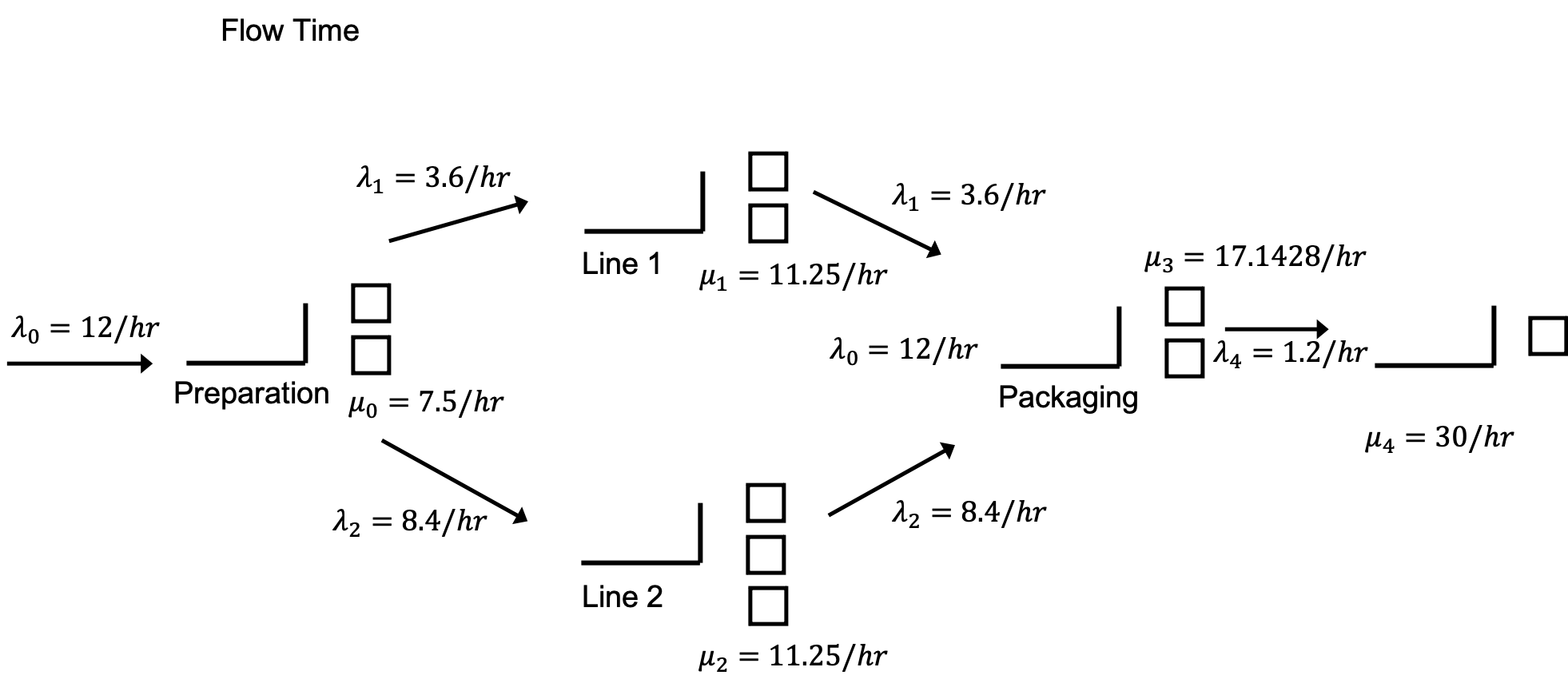
Figure 5.31: Small manufacturing system with flow rates
By examining Figure 5.31 and using a little flow analysis, we can get a pretty good approximation of the results. In the figure, we see each station (preparation, line 1, line 2, packaging, and the palletizer). The flow rate of the parts to each of the stations has also been noted. In what follows each of the stations will be analyzed (individually) and then the overall system will be analyzed using some basic queueing analysis using the results of Appendix C.
The approach is based on determining the rate of flow between the stations and using simple queueing formulas. Let’s start with the preparation station.
5.5.1 Analyzing the Preparation Station
Let \(\lambda_{0}\) be the arrival rate to the preparation station. Let \(\mu_{0}\) be the service rate at the preparation station. This is the rate at which an individual preparation worker works. Let \(\text{MTBA}_{0}\) be the mean time between arrivals for the preparation station and let \(E\lbrack\text{ST}_{0}\rbrack\) be the mean service time at the preparation station. Clearly from the problem description, we have:
\[\lambda_{0} = \frac{1}{\text{MTBA}_{0}} = \frac{1}{5\ \min} \times \frac{60\ \min}{1\ \text{hour}} = 12/\text{hour}\]
\[\mu_{0} = \frac{1}{E\lbrack\text{ST}_{0}\rbrack} = \frac{1}{8\ \min} \times \frac{60\ \min}{1\ \text{hour}} = 7.5/\text{hour}\]
Based on queueing theory, we have that the utilization, \(\rho,\) is:
\[\rho = \frac{\lambda}{c*\mu} = \frac{E\lbrack\text{ST}\rbrack}{c*\text{MTBA}}\]
where \(c\) is the number of servers at the station. For the preparation station, we have:
\[\rho_{0} = \frac{\lambda_{0}}{c\mu_{0}} = \frac{12}{2 \times 7.5} = 0.8\]
From the simulation output results, we see that the utilization of the simulation is exactly that as predicted from the basic flow analysis. Let’s examine the build lines.
5.5.2 Analyzing the Build Lines
In this case, we need to determine the arrival rate to each of the lines. First, we assume that the rate of arrivals out of the preparation station will be the same as the rate of arrivals into the preparation station. Since there is a probabilistic split of the flow to the lines, we can split the rate of parts flowing to line 1 and line 2 based on the probability of selecting the lines. Thus, we have that each line experiences the input rates as follows.
Let \(\lambda_{1}\) be the arrival rate to the line 1 station and let \(\lambda_{2}\) be the arrival rate to the line 2 station.
Let \(p_{1}\) be the probability that line 1 is selected and let \(p_{2}\) be the probability that line 2 is selected.
Thus, \(\lambda_{1} = p_{1} \times\) \(\lambda_{0} = 0.3 \times 12 = 3.6\) per hour and \(\lambda_{2} = p_{2} \times\) \(\lambda_{0} = 0.7 \times 12 = 8.4\) per hour. Now, we need to get the mean service time for the build lines. Because the service time distribution is triangular, we have that the mean of the triangular random variable, X, is:
\[E\left\lbrack X \right\rbrack = \frac{(\min{+ \ \text{mode} + \max)}}{3}\]
Therefore, we can compute the service rate for each of the lines, where \(\text{ST}_{1}\) and \(\text{ST}_{2}\) represent the service time random variable for line 1 and 2, respectively, as follows:
\[\mu_{1} = \frac{1}{E\left\lbrack \text{ST}_{1} \right\rbrack} = \frac{1}{\frac{(2 + 6 + 8)}{3}} = \frac{1}{5.3\overline{3}\ \min} \times \frac{60\ \min}{1\ \text{hour}} = 11.25/\text{hour}\]
\[\mu_{2} = \frac{1}{E\left\lbrack \text{ST}_{2} \right\rbrack} = \frac{1}{\frac{(3 + 6 + 7)}{3}} = \frac{1}{5.3\overline{3}\ \min} \times \frac{60\ \min}{1\ \text{hour}} = 11.25/\text{hour}\]
And, then we can compute the utilization for each of the lines.
\[\rho_{1} = \frac{\lambda_{1}}{c\mu_{1}} = \frac{3.6}{2 \times 11.25} = 0.16\]
\[\rho_{2} = \frac{\lambda_{2}}{c\mu_{2}} = \frac{8.4}{3 \times 11.25} = 0.24\overline{8}\]
Again, these results, match very closely the results from the simulation model. We can also approximate the results for packaging in the same manner.
5.5.3 Analyzing the Packaging Station
Again, we need to compute the incoming flow rate to the packaging station in order to compute the utilization at the station. Let \(\lambda_{3}\) be the arrival rate to the packaging station. If we assume that everything that arrives to each of the two build lines eventually gets to packaging, we can see that \(\lambda_{3} = \lambda_{1} + \lambda_{2} = \lambda_{0} = 12\) per hour.
The mean service time at the packaging station is the sum of the mean wrapping process time and the mean box filling time. The wrapping process has an exponential distribution with a mean of 2 minutes while the filling process has a continuous uniform distribution on the range of 1 to 2 minutes. Thus, using the expected values for these respective distributions, we have:
\[E\left\lbrack ST_{w} \right\rbrack = 2\ \min\]
\[E\left\lbrack ST_{f} \right\rbrack = 1.5\ \min\]
Let \(ST_{3}\) be the service time at the packaging station. Because the time in service at the packaging station include both processing times, we have a utilization calculation as follows:
\[E\left\lbrack ST_{3} \right\rbrack = \ E\left\lbrack ST_{w} \right\rbrack + E\left\lbrack ST_{f} \right\rbrack = 3.5\ \min\]
\[\mu_{3} = \frac{1}{E\left\lbrack \text{ST}_{3} \right\rbrack} = \frac{1}{3.5\ \min} \times \frac{60\ \min}{1\ \text{hour}} = 17.1428\ \text{per}\ \text{hour}\]
\[\rho_{3} = \frac{\lambda_{3}}{c\mu_{3}} = \frac{12}{2 \times 17.1428} = 0.35\]
Again, the results match very closely to the simulation results. With some additional thinking, we can even approximate the utilization of the palletizer.
5.5.4 Analyzing the Palletizing Station
Assuming that all parts that arrive to packaging also arrive to the palletizer, we have a rate of arrivals to the palletizer of 12 per hour. However, we have to wait until there are 10 parts before they are sent to the palletizer. The rate of 12 per hour is a mean time between arrivals of 1 part every 5 minutes. To get 10 parts, it will take on average 50 minutes. Thus, the mean time between arrivals to the palletizer is 50 minutes. Let \(\lambda_{4}\) be the arrival rate to the palletizer. Thus, the arrival rate to the palletizer is
\[\lambda_{4} = \frac{1}{\text{MTBA}_{4}} = \frac{1}{50\ \min}\]
Thus, the utilization for the palletizer should be:
\[\rho_{4} = \frac{\lambda_{4}}{c\mu_{4}} = \frac{E\lbrack ST_{4}\rbrack}{c*\text{MTBA}_{4}} = \frac{2}{1 \times 50} = 0.04\]
Again, this matches quite well with the simulation results. In general, as long as \(\lambda < c\mu\ \)the approximation of utilization will be quite accurate.
5.5.5 Analyzing the Total System Time
We can go even further and approximate the total time spent in the system. If there is no waiting in any of the queues, the approximation is quite simple. We just need to total the time spent in service for the parts. Let \(E\lbrack ST\rbrack\) be the total time spent in service. To compute this value, we can simply add up all of the mean service times for the stations visited. In the case of line 1 and line 2, we can take the weighted average based on the probability that the line is selected as follows:
\[E\left\lbrack \text{ST} \right\rbrack = E\left\lbrack \text{ST}_{0} \right\rbrack + p_{1}E\left\lbrack \text{ST}_{1} \right\rbrack + p_{2}E\left\lbrack \text{ST}_{2} \right\rbrack + E\left\lbrack \text{ST}_{3} \right\rbrack + E\lbrack ST_{4}\rbrack\]
\[E\left\lbrack \text{ST} \right\rbrack = 8 + 0.3 \times 5.3\overline{3} + 0.7 \times 5.3\overline{3} + 3.5 + 2.0 = 18.8\overline{3}\ \text{minutes}\]
This can be easily tested within the simulation model by setting all the resource capacities to “infinite.” If you do this, the results will indicate that the expected time in the system is \(18.8951 \pm 0.06\) with 95% confidence. Clearly, these results are close enough to provide even more credibility to the simulation results.
By using additional queueing theory, we can approximate total time spent at each station by approximating the time spent within the queues and then adding up the total time. This will require additional approximations. For a random variable, \(X\), the squared coefficient of variation is given by:
\[c_{X}^{2} = \frac{\text{Var}(X)}{{(E\left\lbrack X \right\rbrack)}^{2}}\]
Whitt (1983) suggests the following approximation for the queuing time in a GI/G/c queue, where GI is some general independent inter-arrival distribution, G is some general service distribution and c is the number of servers. The approximation has the following form:
\[W_{q}(\text{GI}/G/c) \cong \left( \frac{c_{a}^{2} + c_{s}^{2}}{2} \right)W_{q}(M/M/c)\]
Where \(c_{a}^{2}\) and \(c_{s}^{2}\) represent the squared coefficient of variation of the inter-arrival time distribution and the service time distribution respectively and \(W_{q}(M/M/c)\) is the expected waiting time in a M/M/c queue.
The main difficulty with applying this approximation is determining the variance of the inter-arrival time distribution. In what follows, we will simplify the approach even further and assume that the inter-arrival process at each station is a Poisson process. Thus, the inter-arrival distribution will be assumed to be exponential. Since the variance of an exponential distribution is the square of its mean, the squared coefficient of variation for all the arrival processes will be \(c_{a}^{2} = 1.\) We will just need to compute the squared coefficient of variation for each of the service time distributions associated with each station. To determine the waiting time in queue, we will need the waiting time in queue equations for the M/M/c queueing model. The following table summarizes the formulas for the cases of 1, 2, and 3 servers.
| c = # servers | \(W_{q} =\)Expected Waiting time in Queue |
|---|---|
| 1 | \[\frac{\rho^{2}}{\lambda\left( 1 - \rho \right)}\] |
| 2 | \[\frac{{2\rho}^{3}}{\lambda\left( 1 - \rho^{2} \right)}\] |
| 3 | \[\frac{{9\rho}^{4}}{\lambda\left( 2 + 2\rho - \rho^{2} - 3\rho^{3} \right)}\] |
We can now tabulate the waiting time in the queue for each of the stations. By using the variance associated with each service time distribution, as well as the mean, we can compute the squared coefficient of variation for the service time distribution for each station. The following table summarizes the results. The calculations are left to the reader.
| Station | c | \[\rho = \frac{\lambda}{\text{c}\mu}\] | \[W_{q}(M/M/c)\] | \[c_{a}^{2}\] | \[c_{s}^{2}\] | \[\frac{\left( c_{a}^{2} + c_{s}^{2} \right)}{2}\] | \[W_{q}(\text{GI}/G/c)\] |
|---|---|---|---|---|---|---|---|
| Preparation | 2 | \[0.8\] | \[14.\overline{22}\] | 1 | 1 | 1 | \[14.\overline{22}\] |
| Line 1 Build | 2 | \[0.16\] | \[0.0420\] | 1 | 0.0547 | 0.5274 | 0.0221 |
| Line 2 Build | 3 | \[0.24\overline{8}\] | \[0.0722\] | 1 | 0.0254 | 0.5127 | 0.0370 |
| Packaging | 2 | \[0.35\] | \[0.4886\] | 1 | 0.3333 | 0.6666 | 0.3259 |
| Palletizing | 1 | \[0.04\] | \[0.0722\] | 1 | 0 | 0.5 | 0.0361 |
From these results, we can tabulate an approximation for the total time in the system. Let \(E\lbrack TW_{q}\rbrack\) be the total expected waiting time of a part and \(E\lbrack T\rbrack\) be the expected total time spent in the system for a part. Clearly, we have that, \(E\left\lbrack T \right\rbrack = E\lbrack TW_{q}\rbrack\) +\(\ E\left\lbrack \text{ST} \right\rbrack\), where \(E\lbrack ST\rbrack\) is the total time spent in service for a part. Using the results of the table and taking a weighted average across the waiting time for the two build lines, we can see that the total expected waiting time in queue is:
\[E\left\lbrack TW_{q} \right\rbrack = 14.22 + \left( 0.3 \right)*\left( 0.420 \right) + \left( 0.7 \right)*\left( 0.0722 \right) + 0.4886 + 0.0722 =14.957\]
Thus, the total expected time spent in the system should be approximately, \(E\left\lbrack T \right\rbrack = E\lbrack TW_{q}\rbrack\) +\(\ E\left\lbrack \text{ST} \right\rbrack = 18.83 + 14.957 = 33.79\) minutes. We can compare this value to the simulation result (\(31.73 \pm 0.44\)) with 95% confidence.
Based on this comparison, we can see that the approximation is very good. Again, this should add a great deal of credibility to the reported results. You might think that, in general, simulation models will be “too complex” for such validation methods. Well, sure, I agree that there can be very complex simulation models, but that does not mean that parts of the model would not lend themselves to a simple analysis as demonstrated here. If the individual parts of a simulation model can be validated. Then, as long as we believe that when putting the parts together to form the entire model, it is still valid, then why wouldn’t the overall results not be valid? By verifying and validating individual components of the model, we can build up the credibility in the overall model.
5.5.6 Other Issues for Verification and Validation
As previously noted, verification is about checking if the model or algorithm produces its desired output. Verification is an issue of software quality control. Since computer simulation relies on representing a system within software, we must ensure that we produce software (code) that is error-free. While it is beyond the scope of this book to fully discuss quality control issues within software development, we will not two major approaches that should be applied to simulation model development: 1) testing and 2) debugging.
The test cases should be designed from simple tests to more complicated tests. Test cases can be designed to test individual components of the model. If each component passes its test, then testing all components together should occur. For a stochastic simulation, testing can be performed using statistical tests over the set of test cases that indicate with a high level of confidence that the model produces results that are not significantly different than the expected output. In addition, you might show that the model converges to the expected result. Here, error and relative error, their statistical properties, etc. are important metrics to use to provide overall confidence in the verification process.
Testing a simulation model begins by developing the model in stages. You should first identify the key modeling issues and develop pseudo-code to address those issues. Then, you should map out a logical development process by which the components of the model can be constructed as independently of each other as possible. For example, for the small manufacturing system, the first stage of the model building process would be to simulate the preparation station. We can use DISPOSE modules to dispose of those parts that leave the preparation station and analyze whether or not the preparation station is working correctly. You should identify parts of the system that can be analyzes with very little dependence on the other components. If we only want to check if the logic of the component is working correctly, we can use a simple CREATE module that causes a simpler deterministic arrival pattern and step through the model logic. For example, create a single entity and send it through the model. Does it do what you intended? Force the entity to take a particular path through the system by setting appropriate attributes or changing appropriate DECIDE modules. Does the entity do what it is supposed to do for the test? As noted in Example 5.1 another approach is to set the capacity of all resources to infinity and run the model. Then, you can check if the basic flow time is as expected without any queueing. A staged development process that starts with pseudo-code and tests each stage is critical to ensuring that the model works as intended. Start small. Build small. Test small. And, then integrate the components.
The second recommended method of verification is debugging the model. Use the debugging capability of your software and step through the model. Check edge cases and debug the model. Run the model with watches on variables that stop the model if an invalid condition occurs, trace output through the debugger or by printing out data, watch well designed animation examples that have expected behavior. Animation can be essential to showing that your model is working as intended. Add animation elements that help you determine if your model logic is working. Regardless of whether or not your simulation requires a beautiful animation, you should utilize the basic animation capabilities to verify that your model works. Document what you did for the debugging. State what you did and what you found. The fact that you performed these verification steps is the essential first step in validating your model. Validation is whether or not the model meets its intended purpose. Validation cannot be accomplished unless verification steps have occurred.
Validation cannot be done without convincing the user that the key conceptual elements of the system have been adequately represented in the model. This includes the modeling of the inputs to the system and how the conceptual model has been translated to a computerized representation. This is why documenting the input models and the conceptual model is so important. The old axiom, garbage in equals garbage out is pertinent here. The user must believe that the inputs have been well-modeled. The user must understand what is being modeled.
It is also important that everyone agrees on how the model is intended to be used. If there is no agreement on the conceptual representation or on the model’s use, then validation will be unsuccessful. Validation is predicated on the model representing the system. Thus, validation often involves comparing the output of the model to the output of the real system. If the user of the model cannot tell the difference between model output and real system output, then the model’s representational power is quite high. If you have data from the real system, especially system output performance measures (e.g. throughput, system time, etc.), then you can compare the results of the simulation model to the actual results from the system. You can perform statistical tests to show that the results from the simulation model are not statistically different from the actual system. Again, a staged approach can be used. Do not feel that you have to validate the whole model against the whole system. Perhaps you can collect data on some critical sub-component of the system being modeled. You can then compare the results of your simulation of that critical sub-component to the actual results from that sub-component. Validating each sub-component goes a long way to validating the overall model. It may be easier to collect data from the actual system in stages or in these smaller components. Besides checking if the output matches the actual system output, you should check if the simulation model behaves as expected. The output of the model should react in the same manner as that expected for the real system or the conceptual understanding of how the system works. If you increase the arrial rate, does congestion go up? If not, it is likely something may be misrepresented within your model.
In many situations, the real system does not exist yet. Thus, you will not have real data for validation purposes. This is often the case when simulation is being used to design a system. In such situations, you may be able to approximate the expected performance via “hand” calculations. In this context, you can and should approximation the performance of the simulation model using analytical methods, such as queuing theory. This can provide bounds on the expected performance and add to the credibility of the results. In addition, even if the whole system may not yet exist, perhaps sub-components of the real system exist. If so, you can test output from the sub-components to the associated sub-components of your model. Do not think like you have validate the whole model! Think about how you can validate parts of the model, with the validation of each part contributing the validation of the whole.
Carefully documenting your conceptual model and your assumptions is also an important task for validation. If the user of your model does not understand it through its careful documentation, then they are less likely to believe the results from the model. Performing sensitivity analysis on a set of representative test cases can build credibility in the usage of the model. Validation is ultimately about believability. Does the user believe the results of the model? Validation is whether or not the model/algorithm meets it intended purpose. Verification is about checking if the model/algorithm meets the desired output. You must perform these functions when building a simulation model.