1.3 Types of Systems and Simulation Models
The main purpose of a simulation model is to allow observations about a particular system to be collected as a function of time. So far the word system has been used in much of the discussion, without formally discussing what a system is. According to (Blanchard and Fabrycky 1990) a system is a set of inter-related components working together towards a common objective. The standard for systems engineering provides a deeper definition:
"A system is a composite of people, products, and processes that provide a capability to satisfy stated needs. A complete system includes the facilities, equipment (hardware and software), materials, services, data, skilled personnel, and techniques required to achieve, provide, and sustain system effectiveness." (Command 1991)
Figure1.1 illustrates the fact that a system is embedded within an environment and that typically a system requires inputs and produces output using internal components. How you model a particular system will depend upon the intended use of the model and how you perceive the system. The modeler’s view of the system colors how they conceptualize it. For example, for the emergency room situation, "What are the system boundaries? Should the ambulance dispatching and delivery process be modeled? Should the details of the operating room be modeled?" Clearly, the emergency room has these components, but your conceptualization of it as a system may or may not include these items, and thus, your decisions regarding how to conceptualize the system will drive the level of abstraction within your modeling. An important point to remember is that two perfectly logical and rational people can look at the same thing and conceptualize that thing as two entirely different systems based on their "Weltanschauung" or world view.
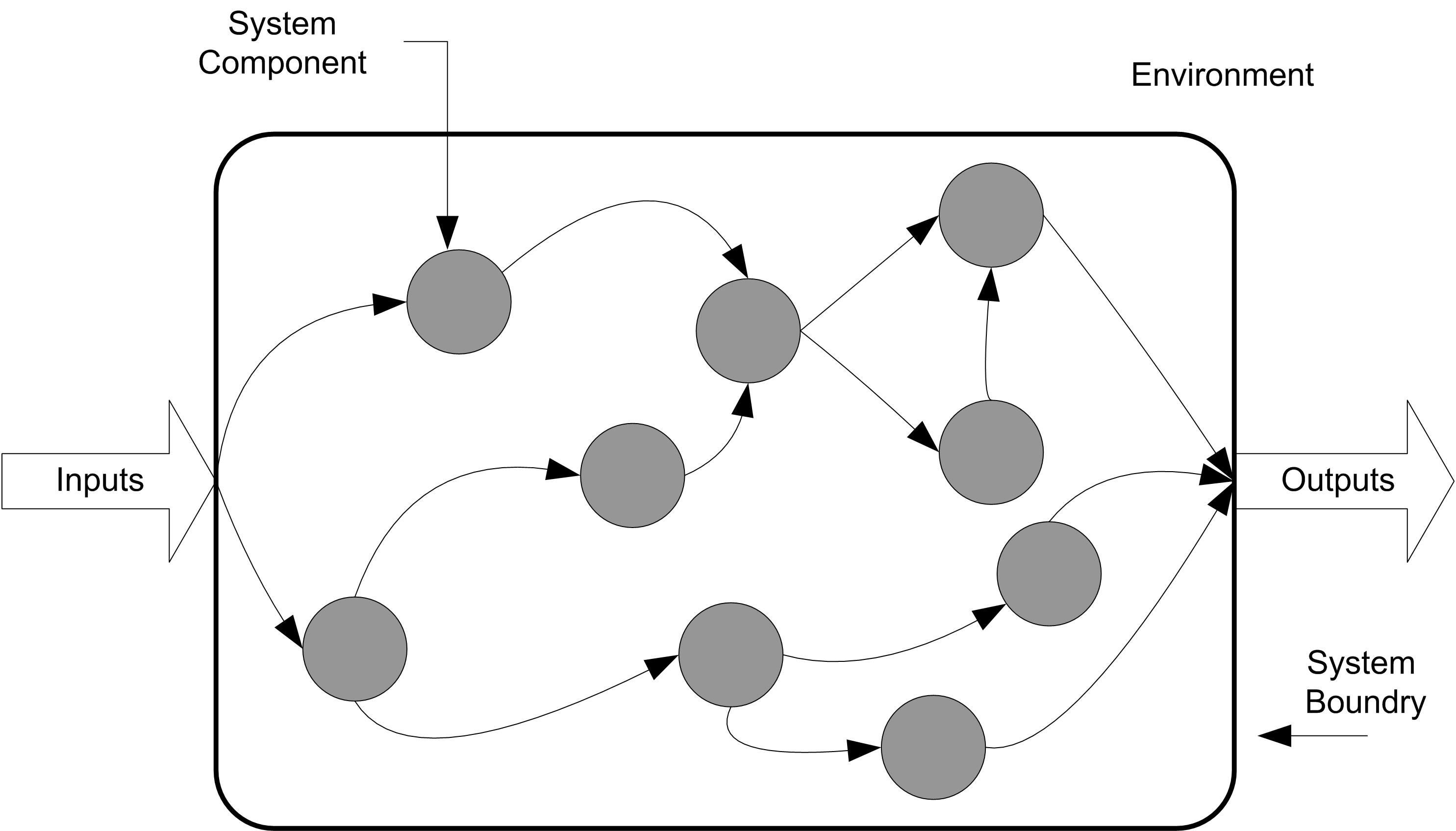
Figure 1.1: Conceptualization of a system
Because how you conceptualize a system drives your modeling, it is useful to discuss some general system classifications. Systems might be classified by whether or not they are man-made (e.g. manufacturing system) or whether they are natural (e.g. solar system). A system can be physical (e.g. an airport) or conceptual (e.g. a system of equations). If stochastic or random behavior is an important component of the system then the system is said to be stochastic, if not then it is considered deterministic. One of the more useful ways to look at a system is whether it changes with respect to time. If a system does not change significantly with respect to time it is said to be static, else it is called dynamic. If a system is dynamic, you might want to consider how it evolves with respect to time. A dynamic system is said to be discrete if the state of the system changes at discrete points in time. A dynamic system is said to be continuous if the state of the system changes continuously with time. This dichotomy is purely a function of your level of abstraction. If conceptualizing a system as discrete, serves our purposes then you can call the system discrete. Figure 1.2 illustrates this classification of systems. This book primarily examines stochastic, dynamic, discrete systems.
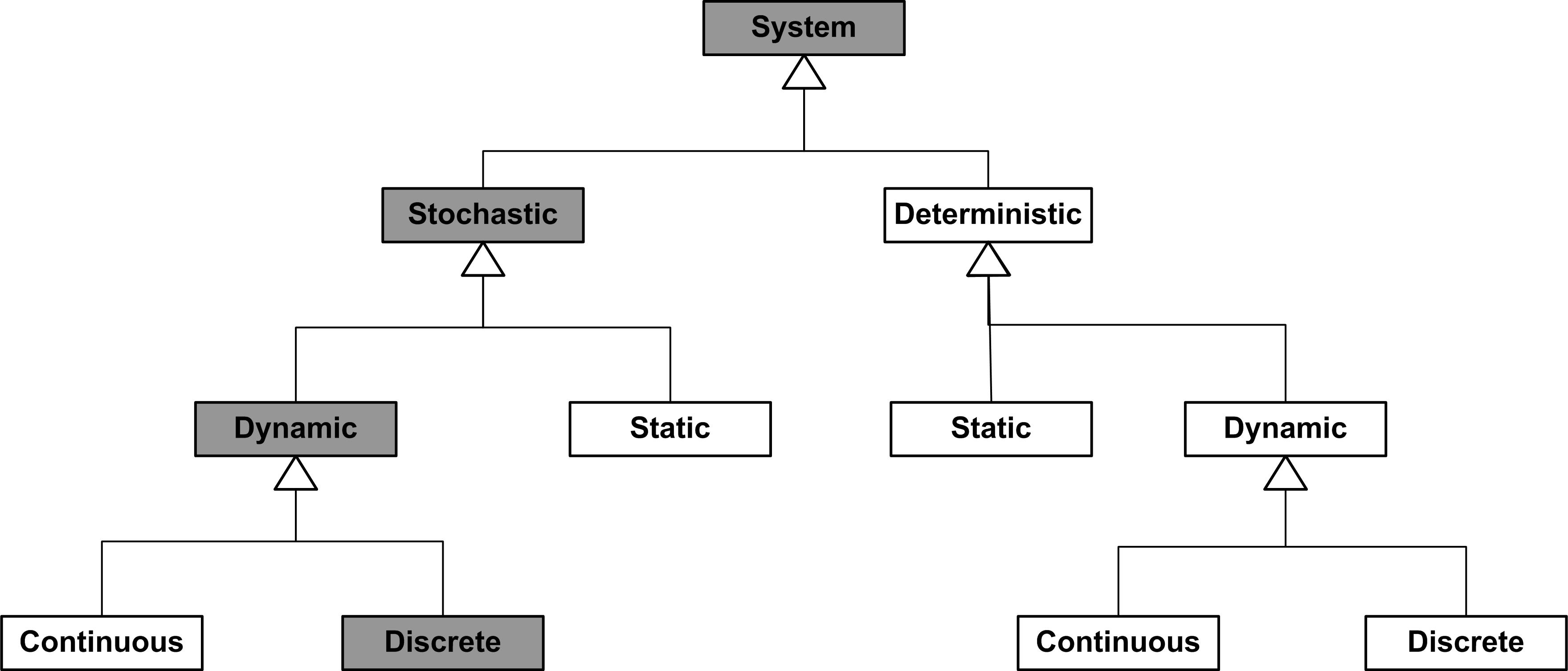
Figure 1.2: General types of systems
The main purpose of a simulation model is to allow observations about a particular system to be gathered as a function of time. From that standpoint, there are two distinct types of simulation: 1) discrete event and 2) continuous.
Just as discrete systems change at discrete points in time, in discrete event simulation observations are gathered at selected points in time when certain changes take place in the system. These selected points in time are called events. On the other hand, continuous simulation requires that observations be collected continuously at every point in time (or at least that the system is described for all points in time). The types of models to be examined in this book are called discrete-event simulation models.
To illustrate the difference between the two types of simulation, contrast a fast food service counter with that of oil loading facility that is filling tankers. In the fast food service counter system, changes in the status of the system occur when a customer either arrives to place an order or when the customer receives their food. At these two events, measures such as queue length and waiting time will be affected. At all the other points in time, these measures remain either unchanged (e.g. queue length) or not yet ready for observation (e.g. waiting time of the customer). For this reason, the system does not need to be observed on a continuous basis. The system need only be observed at selected discrete points in time, resulting in the applicability of a discrete-event simulation model.
In the case of the oil tanker loading example, one of the measures of performance is the amount of oil in each tanker. Because the oil is a liquid, it cannot be readily divided into discrete components. That is, it flows continuously into the tanker. It is not necessary (or practical) to track each molecule of oil individually, when you only care about the level of the oil in the tanker. In this case, a model of the system must describe the rate of flow over time and the output of the model is presented as a function of time. Systems such as these are often modeled using differential equations. The solution of these equations involves numerical methods that integrate the state of the modeled system over time. This, in essence, involves dividing time into small equal intervals and stepping through time.
Often both the discrete and continuous viewpoints are relevant in modeling a system. For example, if oil tanker arrives at the port to be filled, we have an arrival event that changes the state of the system. This type of modeling situation is called combined continuous discrete modeling.
A system and our resulting model depends on how we characterize the state of the system. The state of a system is the set of properties/variables that describe the system at any time \(\{x_1(t), x_2(t), \dots\}\) where \(x_1(t)\) is a variable that represents a system property value at time \(t\). Variables that take on a countable set of values are discrete. Variables that take on an uncountable set of values are said to be continuous. For discrete variables, we can define a mapping from the set of integers to each possible value. Even in the discrete case, there may be an infinite number of values. Continuous variables are represented by the set of real numbers. That is, there are an unaccountably infinite number of possible values that the variable can take on. A discrete system has all discrete variables in its state. A continuous system has all continuous variables in its state. A combined continuous-discrete system has both types of variables in defining its state. Consider an airplane:
If we are interested in the number of parts operating to specification at any time t, then the state is \(\{N_1(t), N_2(t), \dots \}\) where \(N_1(t) = 1\) if part 1 is operating and 0 if part 1 is not operating to specification. The state vector consists of all discrete variables. This is a discrete system.
If we are interested in the temperature of each part at time \(t\), then the state is \(\{T_1(t), T_2(t), \dots \}\), where \(T_1(t)\) is the temperature in Celsius of part 1 at time \(t\), etc. The state vector consists of all continuous variables. This is continuous system.
If we are interested in the velocity of a plane at time \(t\) and the number of wheels deployed at time \(t\), then the state is \(\{v(t), n(t)\}\) where \(v(t)\) is the velocity of the plane in meters/second and \(n(t)\) is \(\{0,1,2,3,4\}\) wheels. Then the state vector consists of both continuous and discrete variables that change with time. This is a combined continuous/discrete system.
Static systems are systems for which time is not a significant factor. In other words, that the state does not evolve over time. Dynamic systems are systems for which system state changes with respect to time. In a deterministic system, the variables are not governed by underlying random processes. In a stochastic system, some of the variables are governed by underlying random processes. Time can change continuously or at discrete points. When time changes only at discrete points in time, we call these points, events.
Some simulation languages have modeling constructs for both continuous and discrete modeling; however, this book does not cover the modeling of continuous or combined continuous discrete systems. There are many useful references on this topic. We will be modeling discrete-event dynamic stochastic systems in this textbook.