6.4 Modeling Balking and Reneging

This situation has multiple types of customers with different priorities, different service times, and in the case of one type of customer, the desire (or ability) to renege from the system. You can find the completed model file for this section in the chapter files under the name, ClinicExample.doe.

Example 6.2 (Walk-in health care clinic) A walk-in care clinic has analyzed their operations and they have found that they can classify their walk-in patients into three categories: high priority (urgent need of medical attention), medium priority (need standard medical attention), and low priority (non-urgent need of medical attention). On a typical day during the period of interest there are about 15 arrivals per hour with (25% being high priority, 60% being medium priority, and the remaining being low priority). The clinic is interested in understanding the waiting time for patients at the clinic. Upon arrival to the clinic the patients are triaged by a nurse into one of the three types of patients. This takes only 2-3 minutes uniformly distributed. Then, the patients wait in the waiting room based on their priority. Patients with higher priority are placed at the front of the line. Patients with the same priority are ordered based on a first-come first served basis. The service time distributions of the customers are given as follows.
Priority Service Time Distribution (in minutes)
High Lognormal(38, 8)
Medium Triangular(16, 22, 28)
Low Lognormal(12, 2)

The clinic has 4 doctors on staff to attend to the patients during the period of interest. They have found through a survey that if there are more than 10 people waiting for service an arriving low priority patient will exit before being triaged. Finally, they have found that the non-urgent (low priority) patients may depart if they have to wait longer than \(15 \pm 5\) minutes after triage. That is, a non-urgent patient may enter the clinic and begin waiting for a doctor, but if they have to wait more than \(15 \pm 5\) minutes (uniformly distributed) they will decide to renege and leave the clinic without getting service. The clinic would like to estimate the following:

  1. the average system time of each type of patient

  2. the probability that low priority patients balk

  3. the probability that low priority patients renege

  4. the distribution of the number of customers waiting in the doctor queue

Solution to Example 6.2

For this problem, the system is the walk-in clinic, which includes doctors and a triage nurse who serve three types of patients. The system must know how the patients arrive (time between arrival distribution), how to determine the type of the patient, the triage time, the service time by type of patient, and the amount of time that a low priority patient is willing to wait.

To determine the type of the patient, a discrete distribution (DISC) can be used. The service time distributions depend on the patient type and can be easily held in an arrayed EXPRESSION. In fact, this information can be held in expressions as illustrated in Figure 6.35. In the DISC() distribution, 1 equals high priority, 2 equals medium priority, and 3 equals low priority. In addition, the system must know the balk criteria for the low priority patients. This information is modeled with variables as illustrated in Figure 6.36.

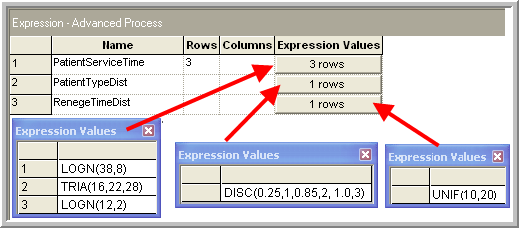
Expressions for walk-in clinic model

Figure 6.35: Expressions for walk-in clinic model

Walk-in clinic VARIABLE module

Figure 6.36: Walk-in clinic VARIABLE module

The entity for this model is the patient. Patients are created according to a particular type, enter the system and then depart. Thus, a key attribute for patients should be their type. In addition, the required performance measures require that the arrival time of the patient be stored so that the total time in the system can later be calculated. There are two resources for this system: triage nurse and doctors, with 1 and 4 units respectively.

The process flow for this system is straightforward, except for the reneging of low priority patients as illustrated in the following pseudo-code.

CREATE patients
ASSIGN myType = PatientTypeDist
DECIDE
    IF (myType == 3) and (NQ(Doctor’s Q) >= vBalkCriteria)
        RECORD balk
        DISPOSE patient
    ELSE
        SEIZE 1 unit of triage nurse
        DELAY for UNIF(2,3) minutes
        RELEASE 1 unit of triage nurse
        // handle reneging patients
        SEIZE 1 unit of Doctors
        DELAY for service based on patient type
        RELEASE 1 unit of Doctors
        RECORD patient’s system time
        DISPOSE
    ENDIF
END DECIDE

In the pseudo-code, the patient is created and then the type is assigned. If the type of patient is of low priority and the doctor’s queue has become to large, then the low priority patient balks. Otherwise, the patient is triaged by the nurse. After triage the patient will wait in the doctor’s queue until their renege time is up or they get served. After the doctor serves the patient statistics are recorded and the patient departs the system.

Modeling the reneging of the patients within requires additional effort. There are no magic dialog boxes or modules that directly handle reneging. The key to modeling the reneging is to remember how Arena processes entities. In particular, from your study in Chapter 2, you saw that no model logic is executed unless an entity is moving through the model. In addition, you know that an entity that is in a queue is no longer moving. Thus, an entity within a queue cannot remove itself from the queue! While this presents a difficulty, it also indicates the solution to the problem.

If the entity that represents the low priority patient cannot remove itself from the queue, then some other entity must do the removal. The only other entities in the system are other patients and it seems both unrealistic and illogical to have another patient remove the reneging patient. Thus, you can only conclude that another (logical) entity needs to be created to somehow implement the removal of the reneging patient.

As you have learned, there are two basic ways to create entities: the CREATE module and the SEPARATE module. Since there is no clear pattern associated with when the patient will renege, this leaves the SEPARATE module as the prime candidate for implementing reneging. Recall that the SEPARATE module works by essentially cloning the entity that goes through it in order to create the specified number of clones. Now the answer should be clear. The low priority patient should clone himself prior to entering the queue. The clone will be responsible for removing the cloned patient from the queue if the delay for service is too long.

Figure 6.37 illustrates the basic ideas for modeling reneging in the form of an activity diagram. Using a SEPARATE module, the patient entity can be duplicated prior to the entity entering the doctor’s queue. Now the two flows can be conceptualized as acting in parallel. The (original) patient enters the doctor queue. If it has to wait, it stops being the active entity, stops moving, and gives control back the event scheduler. At this point, the duplicate (clone) entity begins to move.

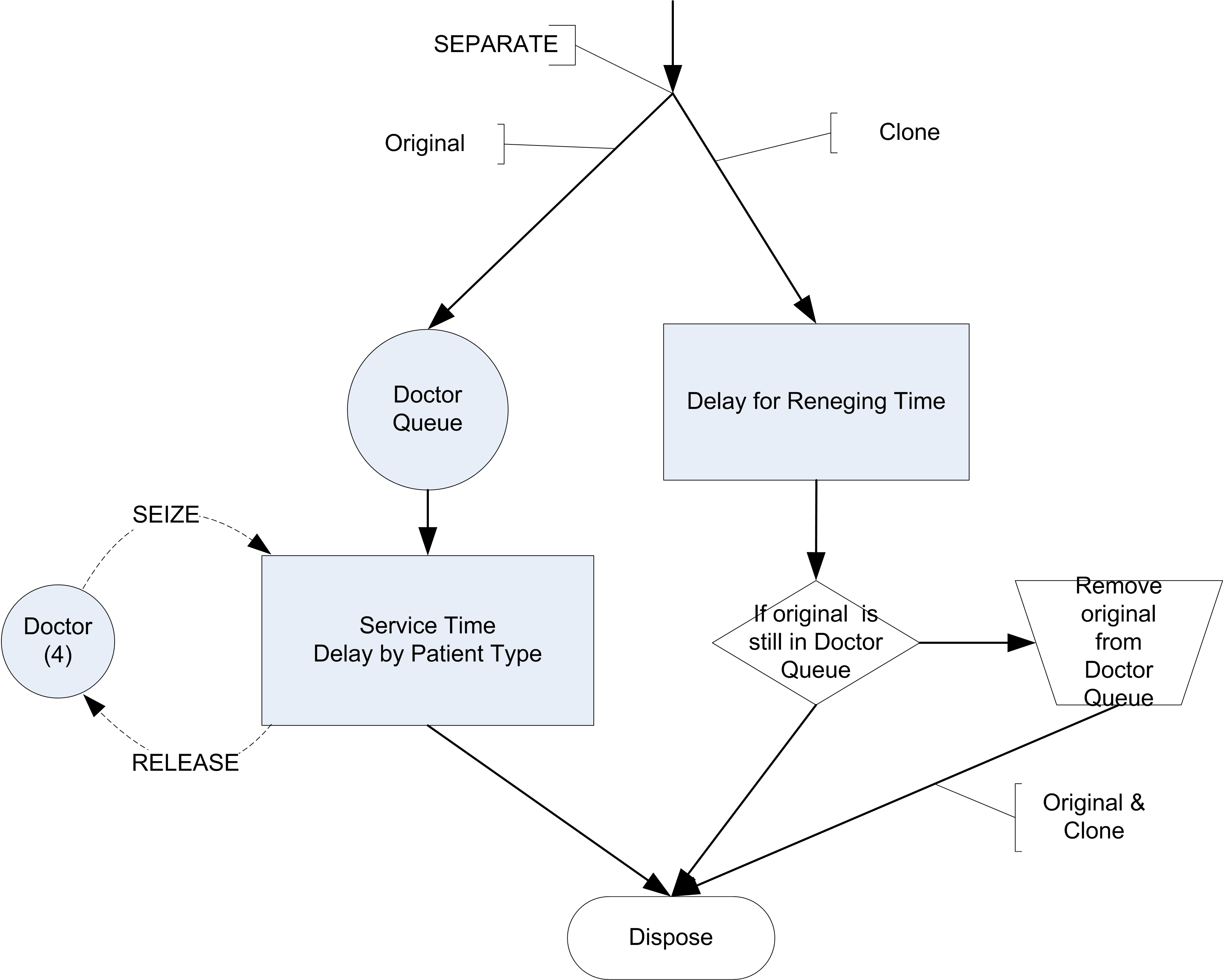
Activity diagram for modeling reneging

Figure 6.37: Activity diagram for modeling reneging

Within the simulation, no actual simulation time has advanced. That is, the clone moves at the same simulated time because it was put in the ready state before becoming the active entity. The now active clone then enters the delay module that represents the time until reneging. This schedules an event to represent this delay and the clone’s progress stops. The event scheduler then allows other entities to proceed through their process flows. One of those other entities might be the original patient entity. If the original entity continues its movement and gets out of the queue before the clone finishes its delay, then it will automatically be removed from the queue by the doctor resource and be processed. If the clone’s delay completes before the original exits the queue, then when the clone becomes the active entity, it will remove the original from the queue and proceed to being disposed. If the clone does not find the original in the queue, then the original must have proceeded and the clone can simply be disposed. One can think of this as the patient, setting an alarm clock (the event scheduled by the duplicate) for when to renege. To implement these ideas within you will need to use the SEPARATE, SEARCH, and REMOVE modules. Now, let’s take a look at the entire model within .

Figure 6.38 provides an overview of the walk-in clinic model that follows closely the previously discussed pseudo-code. The CREATE module has a time between arrival specified as Random(expo) with a mean of 6 minutes. The next ASSIGN module simply assigns the arrival time and the type of patient and then changes the Entity Type and Entity Picture based on some sets that have been defined for each type of patient. This is shown in Figure 6.39.

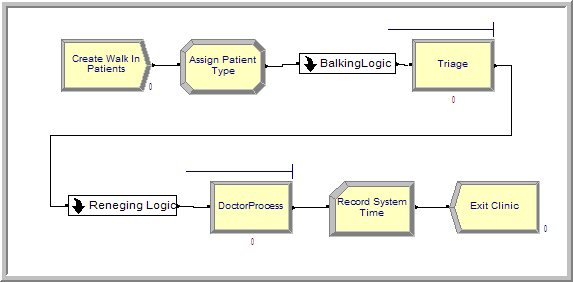
Overview of walk-in clinic model

Figure 6.38: Overview of walk-in clinic model

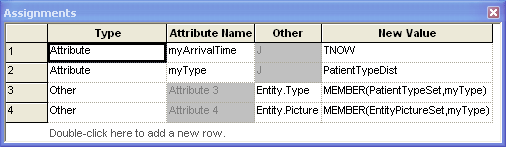
Assigning the type of patient

Figure 6.39: Assigning the type of patient

The Triage and Doctor PROCESS modules are done similarly to how you have implemented many of the prior models. In order to implement the priority for the patients by type, the QUEUE module can be used. In this case the myType attribute can be used with the lowest attribute value as shown in Figure 6.40. You should attempt to build this model or examine the supplied file for all the details.

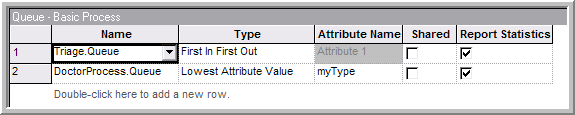
Using the QUEUE module to rank order the queue

Figure 6.40: Using the QUEUE module to rank order the queue

The balking and reneging logic have been placed inside two different sub-models. Balking only occurs for non-urgent patients, so the type of patient is first checked. If the patient is of type non-urgent, whether a balk will occur can be recorded with the expression, NQ(DoctorProcess.Queue) >= vBalkCriteria. This expression evaluates to 1 for true or 0 for false. Thus, the probability of balking can be estimated. The patients who actually balk are then disposed. This is illustrated in Figure 6.41.

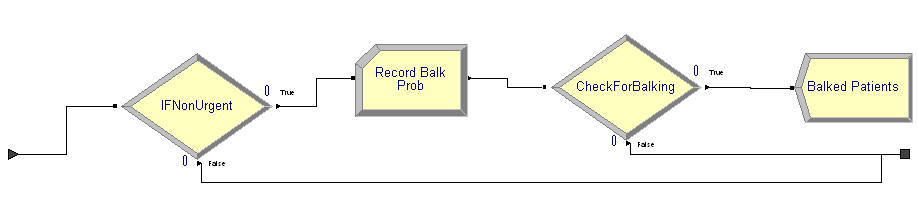
Balking logic sub-model

Figure 6.41: Balking logic sub-model

The reneging logic is more complicated. Figure 6.42 presents an overview of the sub-model logic for reneging.

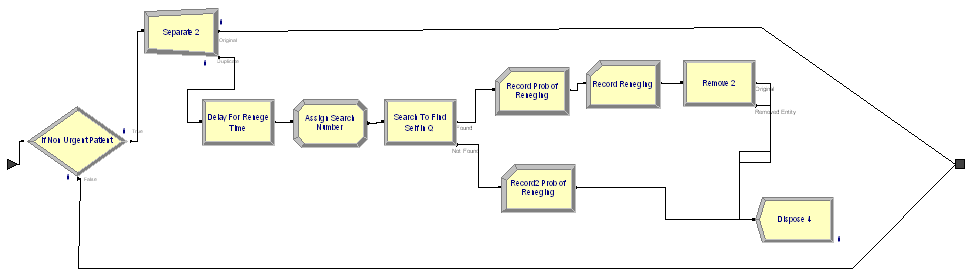
Reneging logic sub-model

Figure 6.42: Reneging logic sub-model

In the logic, the patient’s type is checked to see if the patient is of type non-urgent. If so, the entity is sent to a SEPARATE module. The original entity simply exits the sub-model (to proceed to the queue for the doctor resource). The duplicate then enters the DELAY module that schedules the time until reneging. After exiting the reneging delay, an ASSIGN module is used to set a variable (vSearchNumber) equal to Entity.SerialNumber. Recall that Entity.SerialNumber is a unique number given to each entity when created. When the original entity was duplicated by the SEPARATE module, the duplicate also has this same number assigned. Thus, you can use this number to have the clone search for the original entity within the queue. The SEARCH module allows the searching of a batch, queue, or expression for a particular expression.

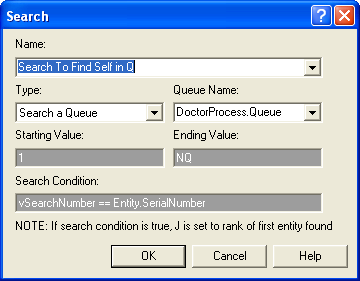
SEARCH module for reneging logic

Figure 6.43: SEARCH module for reneging logic

As illustrated in Figure 6.43, the DoctorProcess.Queue is searched starting at the first entity in the queue (rank 1) to last entity in queue(the entity at rank NQ). The search proceeds to find the first entity where vSearchNumber == Entity.SerialNumber. As the SEARCH module indicates, if the search condition is true the global variable, \(J\), is set to the rank of the first entity satisfying the condition. Thus, after the SEARCH module completes the variable, \(J\), can be used to see if an entity was found. An entity will have been found if \(J > 0\) and not found if \(J = 0\). The SEARCH module has two exit points: one for if the search found something, the other for the case of not finding something. If no entity was found, then the duplicate can simply be disposed because the original is no longer in the queue. If an entity was found then the variable, \(J\), can be used within the REMOVE module to remove the appropriate entity from the queue. The two RECORD modules on both paths after the SEARCH modules use the fact that the Boolean expression, \(J > 0\), will indicate whether or not there was a renege. This is can be observed as an expression in the RECORD modules to collect the probability of reneging as illustrated in Figure 6.44.

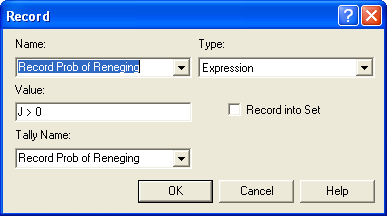
Recording whether reneging occurred

Figure 6.44: Recording whether reneging occurred

If \(J > 0\), then the entity at rank \(J\) can be removed from the DoctorProcess.Queueas illustrated in Figure 6.45. The rest of the model is relatively straightforward and you are encouraged to explore the final dialog boxes.

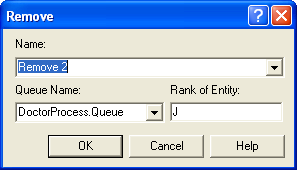
REMOVE module for removing reneging patient

Figure 6.45: REMOVE module for removing reneging patient

Assuming that the clinic opens at 8 am and closes at 6 pm, the simulation was set up for 30 replications to yield the results shown in Figure 6.46. It appears that there is a relatively high chance (about 29%) that a non-urgent patient will renege. This may or may not be acceptable in light of the other performance measures for the system. The reader is asked to further explore this model in the exercises, including the implementation to collect statistics on the number of customers waiting in the doctor queue.

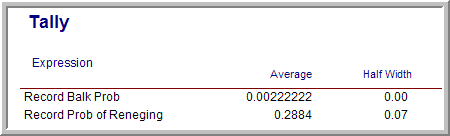
Example output for walk-in clinic model

Figure 6.46: Example output for walk-in clinic model

While some analytical work has been done for queuing systems involving balking and reneging, simulation allows for the modeling of more realistic types of queueing situations as well as even more complicated systems. In the next section, we introduce a very useful construct that enables condition based signaling and control of entity movement. When the entity waits for the condition, it waits in a queue. This permits a wider variety of modeling involving queues.