3.5 Using Sequential Sampling Methods on a Finite Horizon Simulation

In this section, we will discuss how to determine the sample size for a finite horizon simulation by using a sequential sampling method. The new concepts introduced within this section include:

  • Defining an OUTPUT statistic using the Statistics Panel

  • Using a “logical entity” within a model

  • The MREP and NREP global variables

The methods discussed for determining the sample size are based on pre-determining a fixed sample size and then making the replications. If the half-width equation is considered as an iterative function of \(n\).

\[ h(n) = t_{1-(\alpha/2), n - 1} \dfrac{s(n)}{\sqrt{n}} \leq \epsilon \]

Then, it becomes apparent that additional replications of the simulation can be executed until the desired half-with bound is met. This is called sequential sampling. For this method, the sample size of the experiment is not known in advance. That is, the sample size is actually a random variable. The brute force method for implementing this approach would be to run and rerun the simulation each time increasing the number of replications until the criterion is met. By defining an OUTPUT statistic and using the ORUNHALF(Output ID) function, you can have the simulation automatically stop when the criterion is met.

The pseudo-code for this concept is provided here.

CREATE a logical entity at time 0.0
DECIDE IF NREP <= 2 THEN
  DISPOSE
ELSE IF half-width  <= error bound THEN
    ASSIGN MREP = NREP
END DECIDE
DISPOSE

First create a logical entity at time 0.0. Then, use the special variable NREP to check if the current replication executing is less than or equal to 2, if it is dispose of the entity. If the current replication number is more than 2, then check if the half-width is less than or equal to the half-width bound. If it is, then indicate the that maximum number of replications, MREP, has been reached by setting MREP equal to the current replication number, NREP.

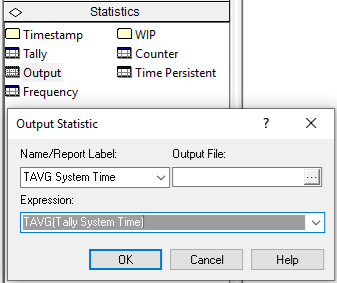
Defining an OUTPUT statistic

Figure 3.30: Defining an OUTPUT statistic

In order to implement this pseudo-code, you must first define an OUTPUT statistic. This is done in Figure 3.30, where the function TAVG(Tally ID) has been used to get the end of replication average for the time spent in both the make and inspection processes. An OUTPUT statistic collects statistics on the expression indicated at the end of a replication. Thus, a single observation, one for each replication, is observed and standard sample statistics, such as the sample average, minimum, maximum, and

This ensures that you can use the ORUNHALF(Output ID) function. The ORUNHALF(Output ID) function returns the current half-width for the specified OUTPUT statistic based on all the replications that have been fully completed. This function can be used to check against the half-width bound.

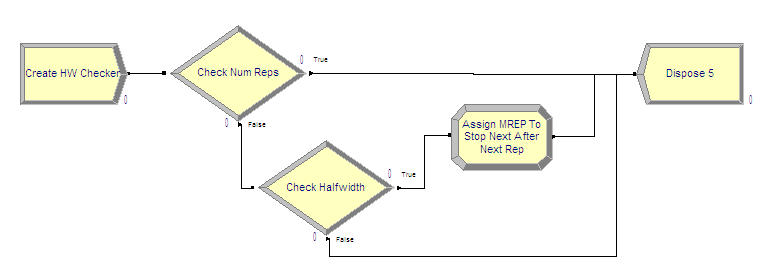
Implemented half-width checking logic

Figure 3.31: Implemented half-width checking logic

Figure 3.31 illustrates the logic for implementing sequential sampling. The CREATE module creates a single entity at time 0.0 for each replication. That entity then proceeds to the Check Num Reps DECIDE module. The special variable, NREP, holds the current replication number. When NREP equals 1, no replications have yet been completed. When NREP equals 2, the first replication has been completed and the second replication is in progress. When NREP equals 3, two replications have been completed. At least two completed replications are needed to form a confidence interval (since the formula for the standard deviation has \(n-1\) in its denominator). Since at least two replications are needed to start the checking, the entity can be disposed if the number of replications is less than or equal to 2. Once the simulation is past two replications, the entity will then begin checking the half-width.

The logic shown in Figure 3.32 shows that the second DECIDE module uses the function ORUNHALF(Output ID) to check the current half-width versus the error bound, which was 1 minute in this case. If the half-width is less than or equal to the bound, the entity goes through the ASSIGN module to trigger the stopping of the replications. If the half-width is larger than the bound, the entity is disposed.

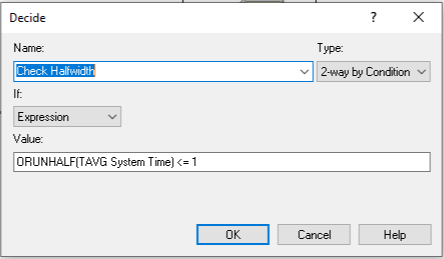
Checking the ORUNHALF function

Figure 3.32: Checking the ORUNHALF function

The special variable called MREP represents the maximum number of replications to be run for the simulation. When you fill out the Run \(>\) Setup dialog and specify the number of replications, MREP is set to the value specified. At the beginning of each replication NREP is checked against MREP. If NREP equals MREP, that replication will be the final replication run for the experiment. Therefore, if MREP is set equal to NREP in the check, the next replication will be the last replication. This actually causes one more replication to be executed than needed, but this cannot be avoided because of how the simulation executes. The only way to make this not happen is to use some VBA code. Figure 3.33 shows the ASSIGN module for setting MREP equal to NREP. Note that the assignment type is Other because MREP is a special variable and not a standard variable (as defined in the VARIABLE module).

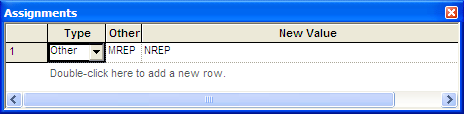
Assigning MREP to NREP

Figure 3.33: Assigning MREP to NREP

This has been implemented in the file STEM_Mixer_Sequential_Sampling.doe. Before running the model, you should set the number of replications (MREP) in the Run \(>\) Setup \(>\) Replication Parameters dialog to some arbitrarily large integer. If you execute the model, you will get the result indicated in Figure 3.34.

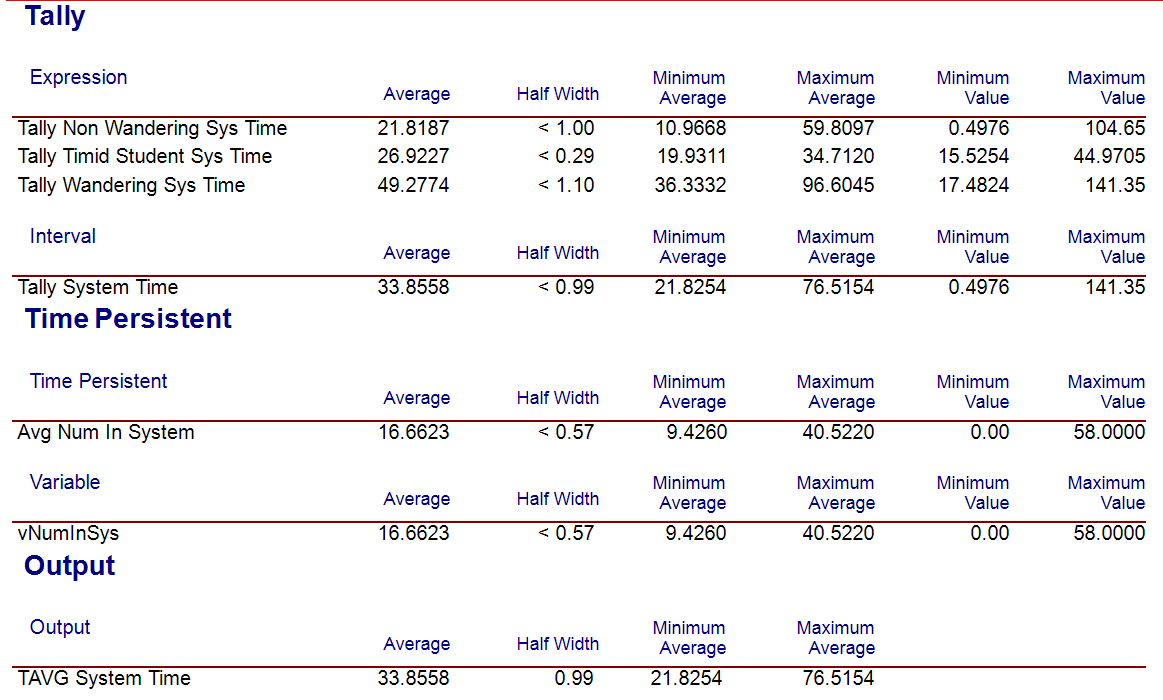
Sequential sampling results for N = 280 Replications

Figure 3.34: Sequential sampling results for N = 280 Replications

In the sequential sampling experiment there were 280 replications. We saw from Table 3.4 that the sample size should be between 219 and 292 in order to meet the half-width criteria based on an initial sample size of 10 replications. The sequential sampling approach iterates to the minimum number of replications to meet the criteria.